【Leetcode Top 100】199. 二叉树的右视图
问题背景
给定一个二叉树的 根节点 r o o t root root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
数据约束
- 二叉树的节点个数的范围是 [ 0 , 100 ] [0,100] [0,100]
- − 100 ≤ N o d e . v a l ≤ 100 -100 \le Node.val \le 100 −100≤Node.val≤100
解题过程
右视图当然考虑三种深度优先遍历的做法,稍微修改一下先序遍历就可以实现。
如果没做过做这个题,记录结果判断条件可能不一定好想,当成模板记下来。多维护一个深度,当深度和结果集长度不匹配时,说明是第一次到达某一层,这时候把当前节点加入到结果集。
具体实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> rightSideView(TreeNode root) {List<Integer> res = new ArrayList<>();dfs(root, 0, res);return res;}private void dfs(TreeNode root, int depth, List<Integer> res) {if(root == null) {return;}if(depth == res.size()) {res.add(root.val);}dfs(root.right, depth + 1, res);dfs(root.left, depth + 1, res);}
}
相关文章:

【Leetcode Top 100】199. 二叉树的右视图
问题背景 给定一个二叉树的 根节点 r o o t root root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。 数据约束 二叉树的节点个数的范围是 [ 0 , 100 ] [0,100] [0,100] − 100 ≤ N o d e . v a l ≤ 100…...

React自学:如何使用localStorage,以及如何实现删除笔记操作
1. 初始化notes 以下这段代码完成了这些操作: 调用 localStorage.getItem("notes") 从浏览器的本地存储中获取名为 “notes” 的数据。使用 JSON.parse 将获取到的字符串解析成数组。如果本地存储中没有 “notes” 数据(返回值为 null&#…...

go语言使用websocket发送一条消息A,持续接收返回的消息
在Go语言中实现一个WebSocket客户端,可以使用gorilla/websocket这个非常流行的库来处理WebSocket连接。下面是一个简单的示例,展示了如何创建一个WebSocket客户端,向服务器发送消息"A",并持续接收来自服务器的响应。 首…...

如何对小型固定翼无人机进行最优的路径跟随控制?
控制架构 文章继续采用的是 ULTRA-Extra无人机,相关参数如下: 这里用于guidance law的无人机运动学模型为: { x ˙ p V a cos γ cos χ V w cos γ w cos χ w y ˙ p V a cos γ sin χ V w cos γ w sin χ…...

C++常见面试题-初级2
1. C和C有什么区别? C是面向对象的语言,而C是面向过程的语言;C引入new/delete运算符,取代了C中的malloc/free库函数;C引入引用的概念,而C中没有;C引入类的概念,而C中没有࿱…...

Spring Security 6 系列之二 - 基于数据库的用户认证和认证原理
之所以想写这一系列,是因为之前工作过程中使用Spring Security,但当时基于spring-boot 2.3.x,其默认的Spring Security是5.3.x。之后新项目升级到了spring-boot 3.3.0,结果一看Spring Security也升级为6.3.0,关键是其风…...

mfc140.dll是什么东西?mfc140.dll缺失的几种具体解决方法
mfc140.dll是Microsoft Foundation Classes(MFC)库中的一个动态链接库(DLL)文件,它是微软基础类库的一部分,为Windows应用程序的开发提供了丰富的类库和接口。MFC库旨在简化Windows应用程序的开发过程&…...

【STM32 Modbus编程】-作为主设备写入多个线圈和寄存器
作为主设备写入多个线圈和寄存器 文章目录 作为主设备写入多个线圈和寄存器1、硬件准备与连接1.1 RS485模块介绍1.2 硬件配置与接线1.3 软件准备2、写入多个线圈2.1 数据格式2.2 发送数据2.3 结果3、写入多个寄存器3.1 数据格式3.2 发送数据3.3 结果本文将实现STM32作为ModBus主…...

Windows安全中心(病毒和威胁防护)的注册
文章目录 Windows安全中心(病毒和威胁防护)的注册1. 简介2. WSC注册初探3. WSC注册原理分析4. 关于AMPPL5. 参考 Windows安全中心(病毒和威胁防护)的注册 本文我们来分析一下Windows安全中心(Windows Security Center…...

微积分复习笔记 Calculus Volume 2 - 4.2 Direction Fields and Numerical Methods
4.2 Direction Fields and Numerical Methods - Calculus Volume 2 | OpenStax...
及其在大型语言模型中的应用)
深入理解旋转位置编码(RoPE)及其在大型语言模型中的应用
文章目录 前言一、 旋转位置编码原理1、RoPE概述2、 复数域内的旋转1、位置编码生成2、 应用位置编码二、RoPE的实现细节1、RotaryEmbedding类设计2、apply_rotary_pos_emb函数3、demo_apply_rotary_pos_emb函数三、完整RoPE代码Demo前言 随着自然语言处理(NLP)领域的快速发…...
内网穿透的应用-在OpenWrt上轻松搭建SFTP服务,安全传输文件不再难!
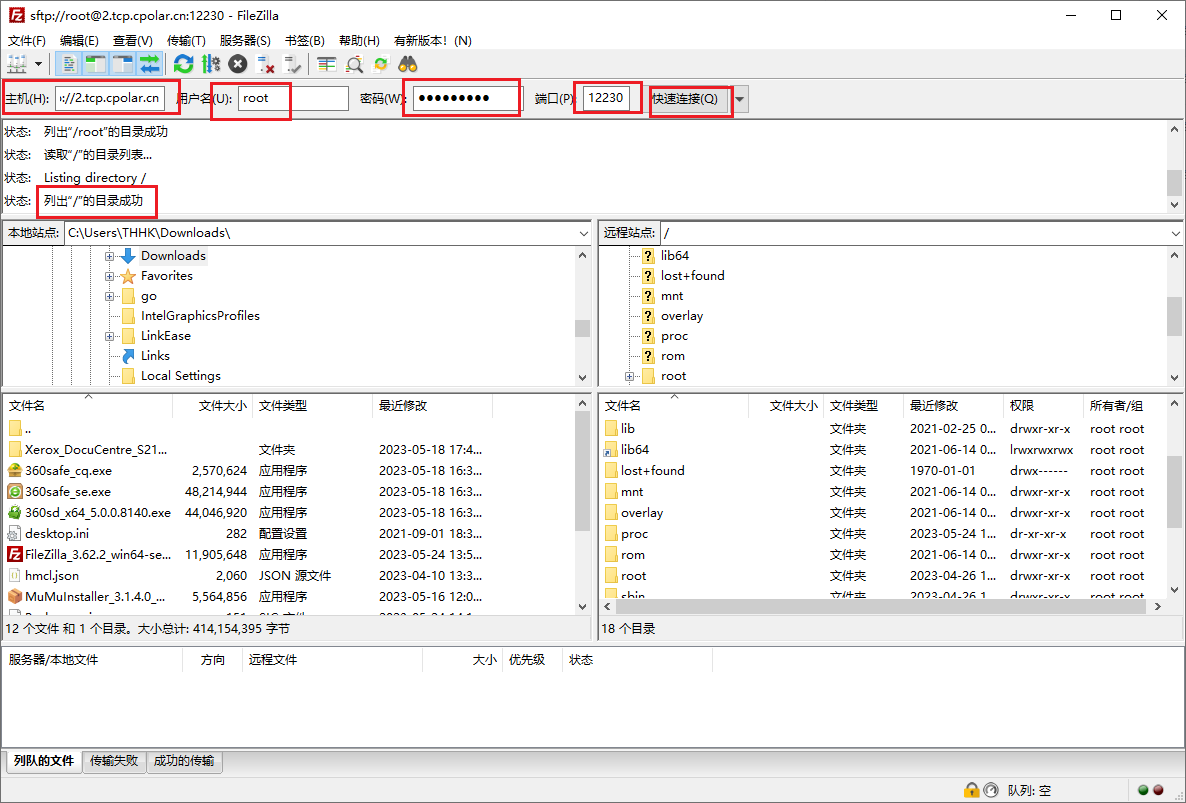
文章目录 前言1. 安装openssh-sftp-server2. 安装cpolar工具3.配置SFTP远程访问4.固定远程连接地址 前言 本次教程我们将在OpenWRT系统上安装SFTP服务,并结合cpolar内网穿透,创建安全隧道映射22端口,实现在公网环境下远程OpenWRT SFTP&#…...

【图像处理lec3、4】空间域的图像增强
目录 1. 空间域图像增强的背景与目标 2. 空间域处理的数学描述 3. 灰度级变换 4. 幂律变换(Power-Law Transformation) 5、 分段线性变换 Case 1: 对比度拉伸 Case 2: 灰度切片 Case 3: 按位切片 6、对数变换(Logarithmic Transform…...

【算法day13】二叉树:递归与回溯
题目引用 找树左下角的值路径总和从中序与后序遍历构造二叉树 今天就简简单单三道题吧~ 1. 找到树左下角的值 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。 假设二叉树中至少有一个节点。 示例 1: 输入: root [2,1,3] 输出: 1 我们…...

上海亚商投顾:创业板指缩量下跌 多只高位股午后跌停
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 市场全天震荡调整,创业板指领跌,高位股开始出现退潮,建设工业、星光股份、…...

单步调试Android Framework——App冷启动
纸上得来终觉浅,绝知此事要躬行。 —— [宋]陆游 基于aosp_cf_x86_64_phone-trunk_staging-eng , 下面是具体断点位置。 第一部分,桌面launcher进程 com.android.launcher3.touch.ItemClickHandler onClickonClickAppShortcutstartAppShor…...

统计一个目录下的文件及目录数量-linux010
要统计一个目录下的文件数量(包括子目录中的文件),可以使用以下命令: 1. 统计所有文件数量(包括子目录) 在终端中运行以下命令: find /path/to/directory -type f | wc -l 解释:…...

spring RestTemplate使用说明
rest-template是spring对httpclient的逻辑封装,它底层还是基于httpclient,所以一些配置其实跟httpclient是强相关的。 基本配置 rest-template可以不带参数,使用默认配置,也可以指定ClientHttpRequestFactory参数,Cl…...

thinkphp:try-catch捕获异常
使用简单的例子,实现了一个简单的try-catch捕获异常的实例 //开始事务Db::startTrans(); try{ //有异常抛出异常 if(存在错误){ throw new \Exception("异常信息"); } // 提交事务 Db::commit(); // 返回成功信息 ... } catch (\…...

shardingsphere分库分表跨库访问 添加分片规则
shardingsphere分库分表跨库访问 添加分片规则 建立 JDBC 环境 创建表 t_order: CREATE TABLE t_order (tid bigint(20) NOT NULL,tname varchar(255) DEFAULT NULL,goods_id bigint(20) DEFAULT NULL,tstatus varchar(255) DEFAULT NULL,PRIMARY KEY (tid) ) E…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
