优化程序中的数据:从数组到代数
前言
我们往往都希望优化我们的程序,使之达到一个更好的效果,程序优化的一个重点就是速度,加快速度的一个好办法就是使用并行技术,但是,并行时我们要考虑必须串行执行的任务,也就是有依赖关系的任务,任务中的重点往往是具体的数据,这些任务中的数据通常具有局部性和关联性。
而数据中数组具有代表性,现在,让笔者从数组开始,谈谈程序数据的优化。
从数据的存储内存开始
我们都知道计算机的基本内存结构如下:
而内存的结构又可以继续划分:
虚拟内存是一个很伟大的发明,它借助内存管理单元(MMU),并利用分页机制将磁盘的一部分模拟为内存使用。它允许计算机使用硬盘空间来扩展实际的物理内存。这使得操作系统能够运行超过实际物理内存容量的程序。
而我们重点关注的地方在cache这里。
cache命中率
cache会从更低一级的内存结构中搬数据,如果数据访问是局部性很强(如访问同一数据块多次),则缓存命中率会较高,如果不命中,那么计算机会跑到下一级内存中寻找数据,这样程序运行效率就会非常低。
优化
得知了这一点后,我们可以考虑改善我们的程序写法了,以数组操作为例:
for(int i = 0; i<= 2; i++){for(int j = i; j<= 2; j++)Z[j][i] = 0;
}
在C语言中,二维数组的内存分布通常是按行优先(Row-major order)存储的,这意味着数组的行是连续存储在内存中的。具体来说,对于一个二维数组 Z,其内存布局是按以下方式排列的:
二维数组的内存分布
假设我们有一个二维数组 Z,其大小为 m 行 n 列。数组元素在内存中的排列顺序如下:
Z[0][0], Z[0][1], ..., Z[0][n-1], Z[1][0], Z[1][1], ..., Z[1][n-1], ..., Z[m-1][0], ..., Z[m-1][n-1]
每一行的元素是连续存储的,然后依次存储下一行的元素。
那么,优化后的遍历方法如下:
for (int j = 0; j <= 2; j++) {for (int i = 0; i <= j; i++) {Z[j][i] = 0;}
}
上面的优化方法相信大家都能琢磨出来,但是,如果稍微改一下呢?
for(int i = 0; i<= 5; i++){for(int j = i; j<= 7; j++)Z[j][i] = 0;
}
按照原程序的遍历:
┌─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┐
│ 0,0 │ 1,0 │ 2,0 │ 3,0 │ 4,0 │ 5,0 │ 6,0 │ 7,0 │
│ │ 1,1 │ 2,1 │ 3,1 │ 4,1 │ 5,1 │ 6,1 │ 7,1 │
│ │ │ 2,2 │ 3,2 │ 4,2 │ 5,2 │ 6,2 │ 7,2 │
│ │ │ │ 3,3 │ 4,3 │ 5,3 │ 6,3 │ 7,3 │
│ │ │ │ │ 4,4 │ 5,4 │ 6,4 │ 7,4 │
│ │ │ │ │ │ 5,5 │ 6,5 │ 7,5 │
│ │ │ │ │ │ │ 6,6 │ 7,6 │
│ │ │ │ │ │ │ │ 7,7 │
└─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┘更好的遍历方法:
┌─────┬─────┬─────┬─────┬─────┬─────
│ 0,0 │
│ 1,0 │ 1,1 │
│ 2,0 │ 2,1 │ 2,2 │
│ 3,0 │ 3,1 │ 3,2 │ 3,3 │
│ 4,0 │ 4,1 │ 4,2 │ 4,3 │ 4,4 │
│ 5,0 │ 5,1 │ 5,2 │ 5,3 │ 5,4 │ 5,5
| 6,0 | 6,1 | 6,2 | 6,3 | 6,4 | 6,5
| 7,0 | 7,1 | 7,2 | 7,3 | 7,4 | 7,5
└─────┴─────┴─────┴─────┴─────┴─────局部性更好的程序如下,此时想要一眼看出来这样写就有点困难了,那我们要怎么推导数组的遍历式呢:
for (int j = 0; j <= 7; j++) {for (int i = 0; i <= (j < 5 ? j : 5); i++) {Z[j][i] = 0;}
}引入线性代数
我们先看看各种值的范围:
i的范围: i>=0, i<=5
j的范围: j>=i, j<=7
尝试把它们写成线性方程:
1*i + 0*j + 0 >= 0
-1*i + 0*j + 5 >= 0-1*i + j + 0 >= 0
0*i + -1*j + 7 >= 0矩阵如下:
| 1 0 | | i | >= | 0 |
| -1 0 | * | j | >= | -5 |
| -1 1 | >= | 0 |
| 0 -1 | >= | -7 |现在我们得到了矩阵,我们可以进一步得到多面体,先回顾一下矩阵与多面体的关系:
线性约束表示多面体
多面体可以通过一组线性不等式来定义,这些不等式可以表示为矩阵和向量的形式。例如,对于一个包含 n个变量的多面体,可以用一个 m×n 的矩阵A和一个m维的向量 b来表示:
Ax <= b
其中,x是变量向量,约束条件定义了多面体的边界。
顶点表示
多面体的顶点可以通过求解线性方程组(通常涉及矩阵的逆或者伪逆)来获得。这些顶点是满足约束条件的解。
矩阵操作多面体
线性变换
通过矩阵乘法,可以对多面体进行线性变换(如旋转、缩放、平移等)。例如,如果矩阵M描述了一个线性变换,那么多面体中的每一个点 x在变换后的新位置可以表示为Mx。
仿射变换
仿射变换是线性变换的推广,包括线性变换和平移。可以用如下形式表示:
y=Mx+t
其中,MM 是线性变换矩阵,t是平移向量。
好吧,其实矩阵和多面体与接下来要讲的算法也没多大关系,笔者只是想说明如何从不等式推导到线性代数并扩展到多面体和高维空间体的。
使用Fourier-Motzkin算法
Fourier-Motzkin算法是一种经常在多面体中用于求解线性不等式系统的消去算法,概括如下:
选择消去变量: 选择一个变量 xi作为消去变量。
分类不等式: 将所有不等式分为三类:
- 包含 Xi的不等式,且 Xi的系数为正。
- 包含 Xi的不等式,且 Xi的系数为负。
- 不包含 Xi的不等式。
生成新不等式: 通过将第一类不等式和第二类不等式配对,消去 Xi
组合不等式: 将生成的新不等式与不包含 xi的不等式组合,得到一个新的线性不等式系统。
重复步骤: 对新的线性不等式系统重复上述步骤,直到所有变量都被消去。
应用该算法,我们重新得到范围:
0<=j, 0 <=5
j<=7
那么i和j的范围如下:
L(i):0
U(i):5,jL(i):0
U(J):7
有了这个范围,我们可以得到:
for (int j = 0; j <= 7; j++) {for (int i = 0; i <= min(5,j); i++) {Z[j][i] = 0;}
}
也就是:
for (int j = 0; j <= 7; j++) {for (int i = 0; i <= (j < 5 ? j : 5); i++) {Z[j][i] = 0;}
}
总结
从程序中的优化出发,由程序存储引出cache,再由cache命中率引出数据局部性的重要性,为了提高数据局部性,必须改变循环遍历方法。为了改变循环遍历方法,由不等式引出线性代数,再由线性代数引出多面体,最后使用算法计算约束,得到具有良好局部性的程序。
其实没啥好总结的,只写了一小段,还没写完开头呢,不过先更到这,该上床睡觉了。
相关文章:

优化程序中的数据:从数组到代数
前言 我们往往都希望优化我们的程序,使之达到一个更好的效果,程序优化的一个重点就是速度,加快速度的一个好办法就是使用并行技术,但是,并行时我们要考虑必须串行执行的任务,也就是有依赖关系的任务&#…...

【电商搜索】CRM: 具有可控条件的检索模型
【电商搜索】CRM: 具有可控条件的检索模型 目录 文章目录 【电商搜索】CRM: 具有可控条件的检索模型目录文章信息摘要研究背景问题与挑战如何解决核心创新点算法模型实验效果(包含重要数据与结论)相关工作后续优化方向 后记 https://arxiv.org/pdf/2412.…...

使用 ffmpeg 拼接合并视频文件
按顺序拼接多个视频文件 1、创建文件清单 创建一个文本文件 filelist.txt,列出所有要合并的视频文件。 格式如下: file path/to/video1.mp4 file path/to/video2.mp4 file path/to/video3.mp42、合并文件 下载FFmpeg,然后使用FFmpeg进行…...
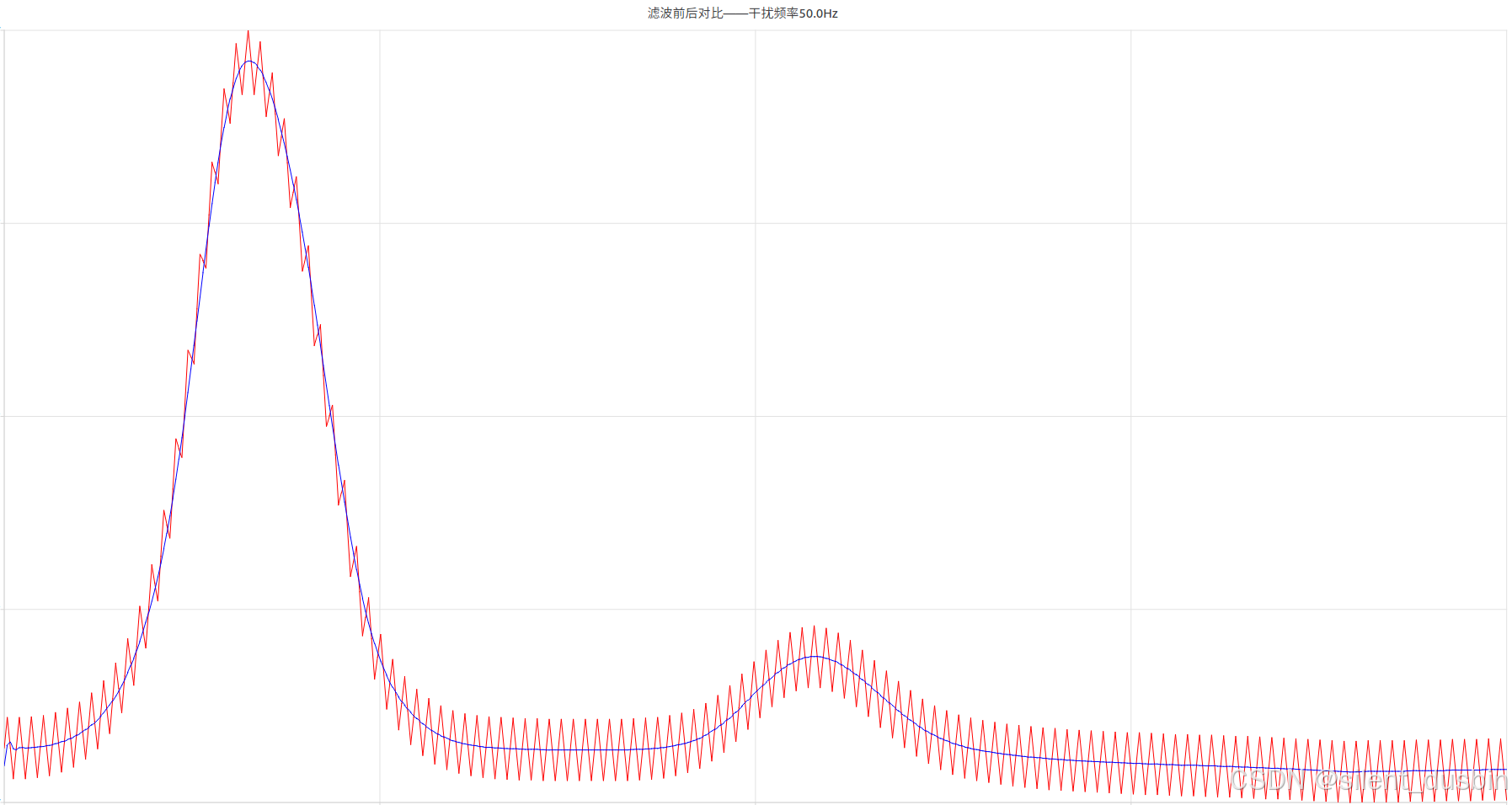
【信号滤波 (上)】傅里叶变换和滤波算法去除ADC采样中的噪声(Matlab/C++)
目录 一、ADC采样的噪声简介1.1 常见的ADC噪声来源 二、信号的时域到频域转换2.1 傅里叶变换巧记傅里叶变换 三、傅里叶变换和滤波算法工程实现3.1 使用Matlab计算信号时域到频域的变换3.2 使用Matlab去除特定频点噪声寻找峰值算噪声频率构建陷波滤波器滤除噪声频点陷波滤波器与…...

Idea内,光标显示问题
键盘误触导致光标显示为白色块 解决方式 任选其一 键盘敲击 Ins 键(既 insert 键)Shift 0(数字零)...

回顾 python3中字符串
一. 简介 前面学习了 python3中的字符串, 本文回顾一下 python3中的字符串。 二. python3中的字符串 1. 创建字符串 字符串是 python中最常用的数据类型。我们可以使用引号( 或者 " )来创建字符串。 创建字符串很简单,…...

代码随想录day23 | leetcode 39.组合总和 40.组合总和II 131.分割回文串
39.组合总和 Java class Solution { List<List<Integer>> result new ArrayList<>();LinkedList<Integer> path new LinkedList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sor…...
备考实战之分支结构(switch语句))
全国青少年信息学奥林匹克竞赛(信奥赛)备考实战之分支结构(switch语句)
if语句处理多个分支时需要用if-else if结构,分支越多,嵌套的if语句层就越多,程序不但庞大、复杂,理解起来也比较困难。在C编程中,针对有些问题除了使用if-else if结构之外,还有switch语句也可以实现&#x…...

R机器学习:决策树算法的理解与实操
今天继续给大家介绍决策树算法,决策树本身是一种非常简单直观的机器学习算法,用于做分类或回归任务。它就像我们平常做决定时的过程,通过逐步排除可能的选项,最终得出结论。 A decision tree is a flowchart-like structure used …...

解锁高效学习之道:从认知升级到实践突破
目录 学习之困:探寻低效的根源 (一)迷茫之境:目标缺失的困扰 (二)表象之迷:浅尝辄止的学习 (三)行动之阻:执行力的短板 认知重塑:明晰学习的本…...

2024年12月CCF-GESP编程能力等级认证Python编程三级真题解析
本文收录于专栏《Python等级认证CCF-GESP真题解析》,专栏总目录:点这里,订阅后可阅读专栏内所有文章。 一、单选题(每题 2 分,共 30 分) 第 1 题 2024年10月8日,诺贝尔物理学奖“意外地”颁给了两位计算机科学家约翰霍普菲尔德(John J. Hopfield)和杰弗里辛顿(Geof…...

.NET Core 中使用 C# 获取Windows 和 Linux 环境兼容路径合并
在 .NET Core 中使用 C# 处理路径合并并确保在 Windows 和 Linux 环境中都能正常工作,可以使用 System.IO.Path 和 System.IO.Path.Combine 方法。它们是跨平台的,能够根据操作系统自动处理路径分隔符。可以通过 System.Runtime.InteropServices.Runtime…...
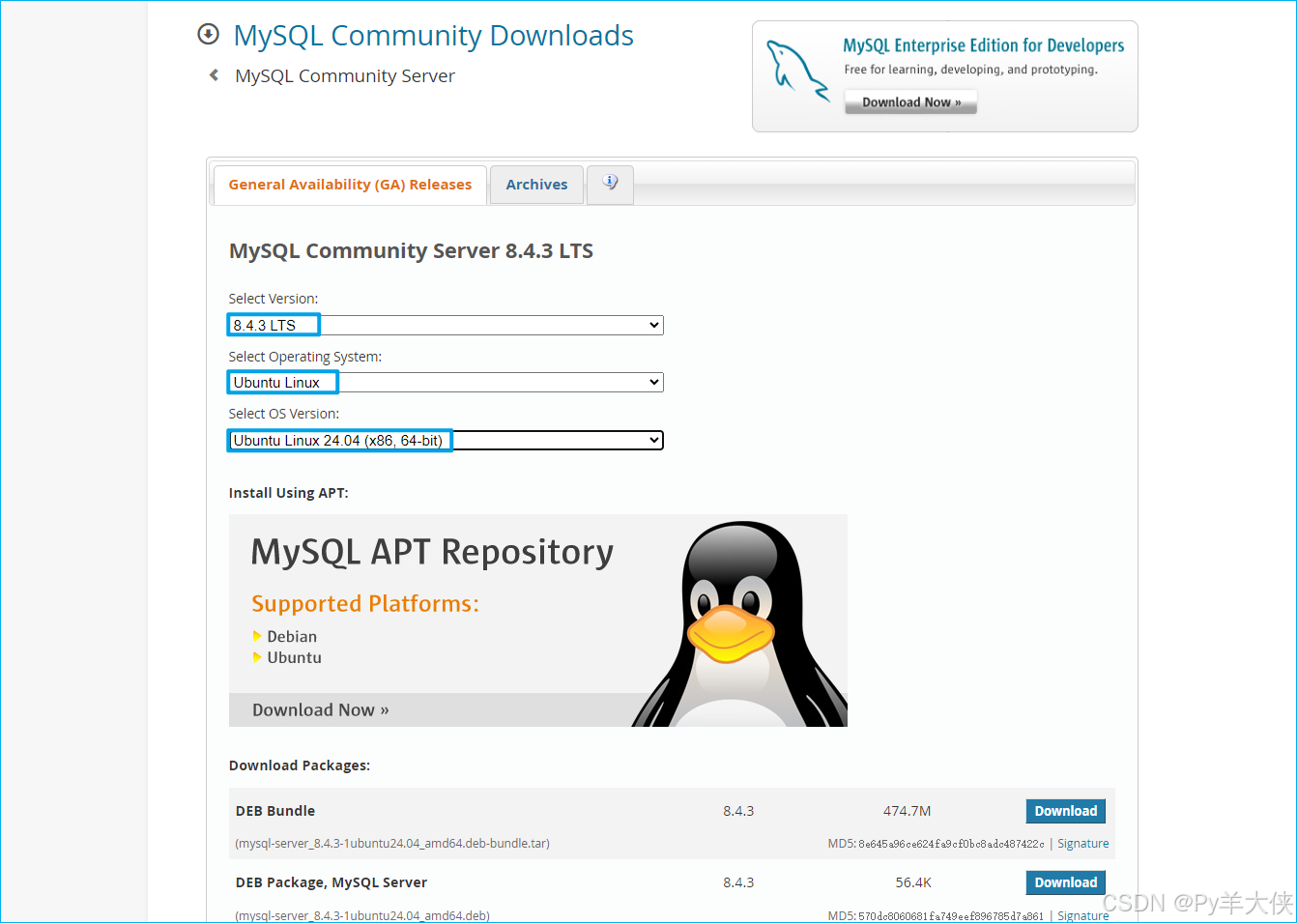
【SH】Ubuntu Server 24服务器搭建MySQL数据库研发笔记
文章目录 搭建服务器在线安装1. 更新软件包列表2. 安装MySQL3. 检查MySQL状态4. 修改密码5. 新增用户6. 设置局域网访问 离线安装下载安装包 常用命令参考文档在线安装日志 搭建服务器 作者羊大侠搭建的是 Ubuntu Server 24.04 LTS 服务器环境 搭建参考文档:【SH】…...
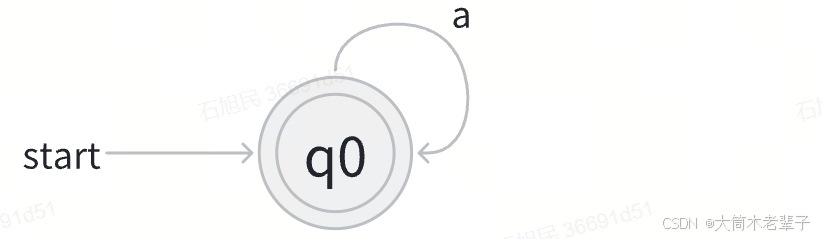
编译原理复习---正则表达式+有穷自动机
适用于电子科技大学编译原理期末考试复习。 1. 正则表达式 正则表达式(Regular Expression,简称regex或regexp)是一种用于描述、匹配和操作文本模式的强大工具。它由一系列字符和特殊符号组成,这些字符和符号定义了一种搜索模式…...
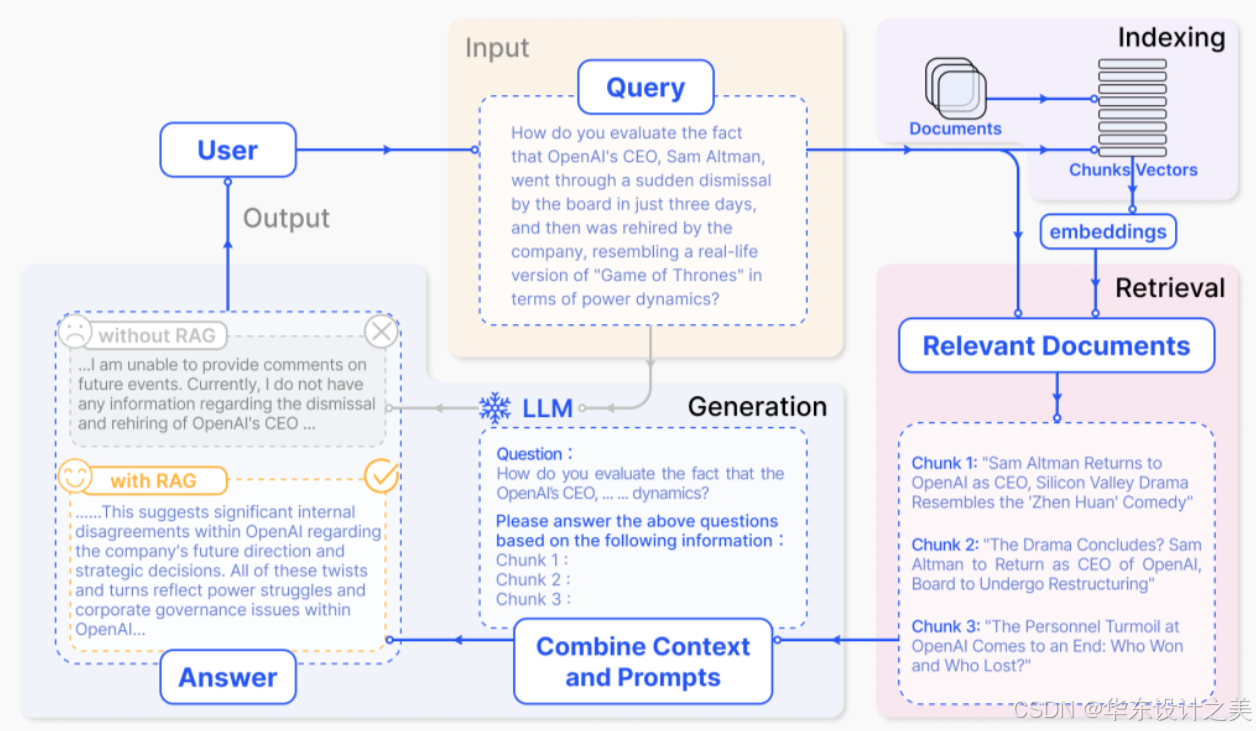
知识图谱+RAG学习
GraphRAG(Graph-based Retrieval-Augmented Generation)是微软在2024年推出的一项开源技术,旨在通过结合知识图谱和检索增强生成(RAG)方法,为大型语言模型(LLM)的数据处理提供全新解…...
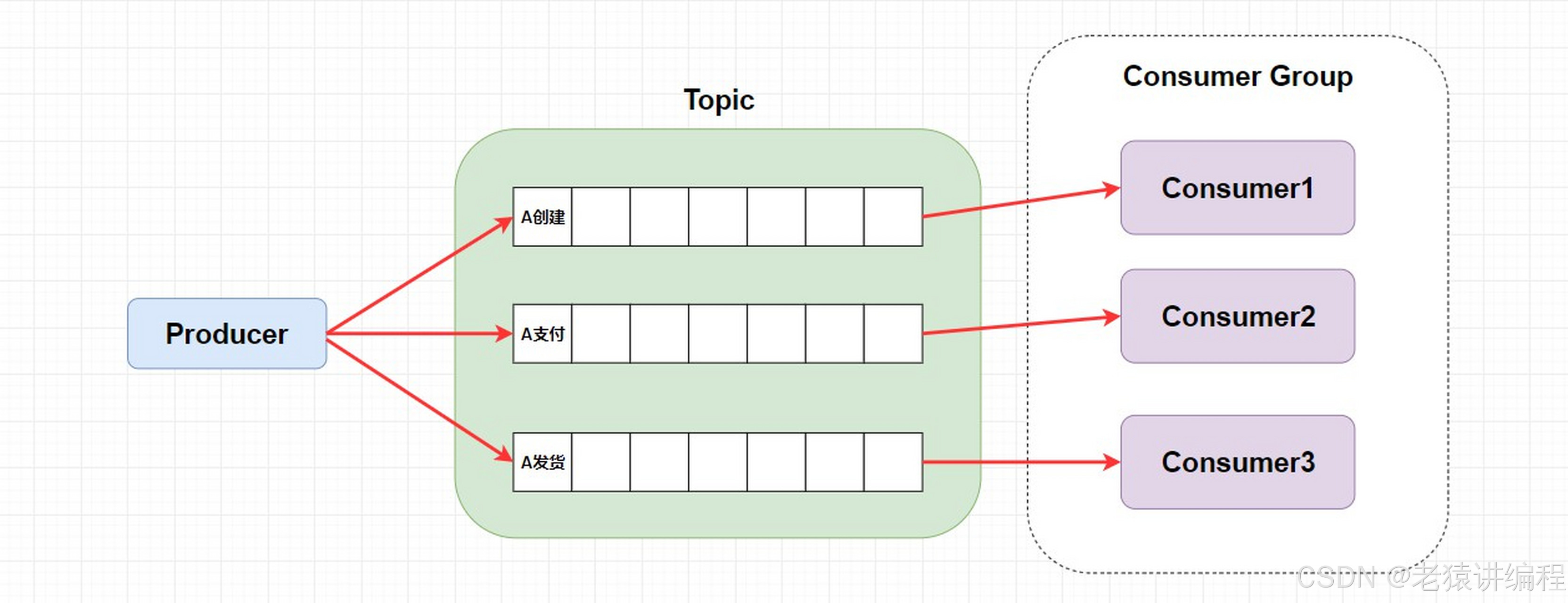
消息队列技术的发展历史
消息队列技术的演进历程宛如一幅波澜壮阔的科技画卷,历经多个标志性阶段,各阶段紧密贴合不同的技术需求与市场风向,下面为您详细道来。 第一阶段:消息中间件的起源(1970 年代末期 - 1980 年代中期) 在计算…...

每天40分玩转Django:Django部署
Django部署 一、今日学习内容概述 学习模块重要程度主要内容生产环境配置⭐⭐⭐⭐⭐settings配置、环境变量WSGI服务器⭐⭐⭐⭐⭐Gunicorn配置、性能优化Nginx配置⭐⭐⭐⭐反向代理、静态文件安全设置⭐⭐⭐⭐⭐SSL证书、安全选项 二、生产环境配置 2.1 项目结构调整 mypr…...
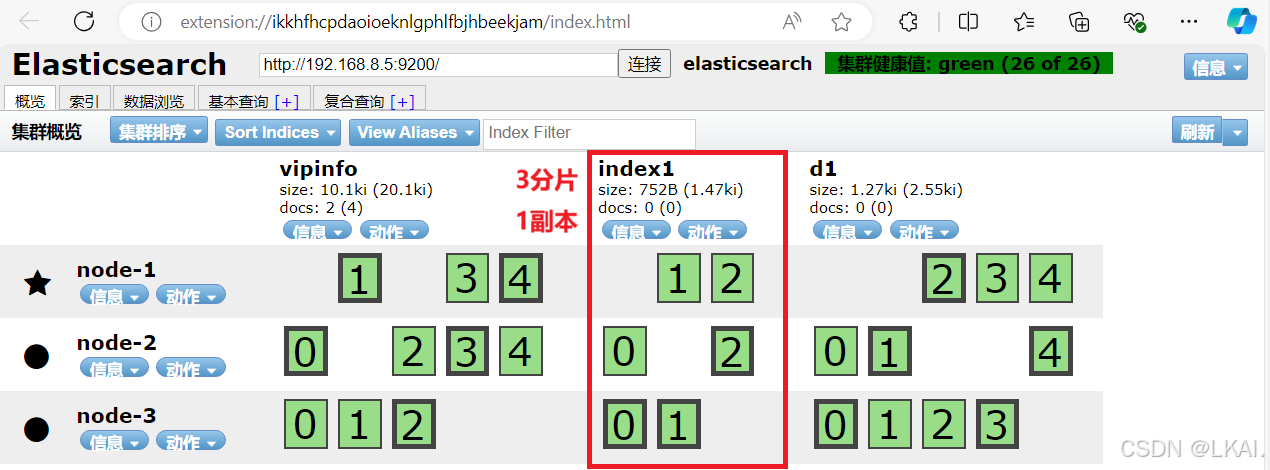
搭建Elastic search群集
一、实验环境 二、实验步骤 Elasticsearch 是一个分布式、高扩展、高实时的搜索与数据分析引擎Elasticsearch目录文件: /etc/elasticsearch/elasticsearch.yml#配置文件 /etc/elasticsearch/jvm.options#java虚拟机 /etc/init.d/elasticsearch#服务启动脚本 /e…...
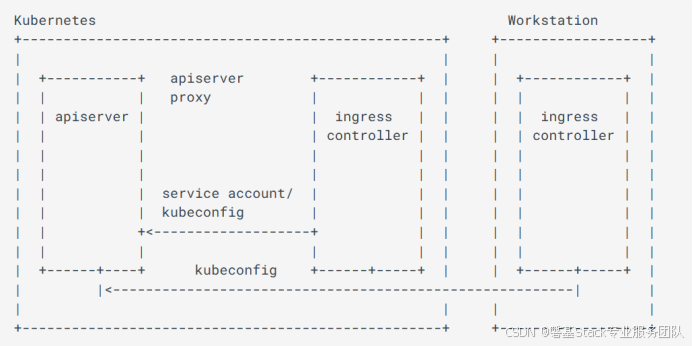
解析 Ingress-Nginx 故障:排查思路与方法
文章目录 一、什么是Ingress-Nginx二、故障排除1.1Ingress-Controller日志和事件检查 Ingress 资源事件检查 Nginx 配置检查使用的服务是否存在调试日志 1.2对 Kubernetes API 服务器的认证服务认证服务账户Kube-Config 1.3使用GDB和Nginx1.4在 Nginx 4.2.5 或其他版本…...

2024 楚慧杯 re wp
go_bytes 附件拖入ida 输入长度为0x28,每两位字符的4bit拼接 与一个常量值经过运算后的值进行异或,并且判断是否相等 脚本 bouquet 附件拖入ida。简单去一下花 构建了一个二叉树,然后递归调用函数 重新排列一下再层序遍历读出即可 zistel 附件…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
