“LoRA技术中参数初始化策略:为何A参数采用正态分布而B参数初始化为0”
在LoRA(Low-Rank Adaptation)中,参数A和B的初始化策略是经过精心设计的,以确保模型训练的稳定性和有效性。具体来说,参数A通常被初始化为正态分布,而参数B则初始化为0。这样的设计有以下几个优点:
-
保持原始模型行为:当B初始化为0时,新增的部分对原始权重的影响为零,从而不会破坏预训练模型的初始性能。这允许模型在训练初期完全保持原始模型的行为,从而为学习差异提供了一个平滑的起步。
-
确保初始梯度的有效传播:正态分布初始化有助于在训练初期确保梯度有效传播,避免梯度消失或爆炸的问题。
-
提供足够的随机性:正态分布的随机初始化为模型提供了足够的随机性,从而能够探索更广泛的参数空间,增加了模型找到最优解的可能性。
-
平衡训练初期的影响:正态分布初始化的值一般较小,结合B初始化为零矩阵,可以在训练初期确保新增的偏置矩阵对原始预训练权重的影响为零,从而避免破坏预训练模型的初始性能。
-
避免梯度消失:如果B和A全部初始化为零矩阵,缺点是很容易导致梯度消失。
-
避免过多噪声:如果B和A全部正态分布初始化,那么在模型训练开始时,就会容易得到一个过大的偏移值,从而引起太多噪声,导致难以收敛。
综上所述,LoRA中参数A的正态分布初始化和参数B的零初始化是为了在保持预训练模型性能的同时,有效地引入新的参数进行微调,从而实现模型的高效适应新任务。
相关文章:

“LoRA技术中参数初始化策略:为何A参数采用正态分布而B参数初始化为0”
在LoRA(Low-Rank Adaptation)中,参数A和B的初始化策略是经过精心设计的,以确保模型训练的稳定性和有效性。具体来说,参数A通常被初始化为正态分布,而参数B则初始化为0。这样的设计有以下几个优点࿱…...

C语言初阶力扣刷题——349. 两个数组的交集【难度:简单】
1. 题目描述 力扣在线OJ题目 给定两个数组,编写一个函数来计算它们的交集。 示例: 输入:nums1 [1,2,2,1], nums2 [2,2] 输出:[2] 输入:nums1 [4,9,5], nums2 [9,4,9,8,4] 输出:[9,4] 2. 思路 直接暴力…...

理解动手学深度学习的自编包d2l
跟着李沐的《动手学深度学习-PyTorch版》入门Python编程和Pytorch框架,以前是重度Matlab用户,对于Python里的各种包很不习惯。特别是,本书还自己做了一个名为d2l包,有几个问题很是困惑。今天终于弄明白了,写在这里&…...
)
RK3568使用opencv(使用摄像头捕获图像数据显示)
文章目录 一、opencv相关的类1. **cv::VideoCapture**2. **cv::Mat**3. **cv::cvtColor**4. **QImage**5. **QPixmap**总结 二、代码实现 一、opencv相关的类 1. cv::VideoCapture cv::VideoCapture 是 OpenCV 中用于视频捕捉的类,常用于从摄像头、视频文件、或者…...

OpenEuler学习笔记(十六):搭建postgresql高可用数据库环境
以下是在OpenEuler系统上搭建PostgreSQL高可用数据环境的一般步骤,通常可以使用流复制(Streaming Replication)或基于Patroni等工具来实现高可用,以下以流复制为例: 安装PostgreSQL 配置软件源:可以使用O…...

数学平均数应用
给定一个长度为 n 的数组 a。在一次操作中,你可以从索引 2 到 n−1中选择一个索引i,然后执行以下两个操作之一: 将 a[i−1] 减少 1,同时将 a[i1] 增加 1。 将 a[i1] 减少 1,同时将 a[i−1] 增加 1。 在每次操作后&…...

元旦和春节取名的历史变迁
在中国漫长的历史长河中的春节,真要追溯起来也只有一百多年历史——是从晚清时期才逐渐出现在国人的生活里的,而且那时不叫“春节”而叫“元旦”。只不过随着历史的发展过程,“过年”这个名词也一直在演变,直至1949年最终才定下来…...

USB鼠标的数据格式
USB鼠标的数据格式由HID(Human Interface Device)协议定义,通常包含3个字节的标准数据,具体格式如下: 字节内容描述第1字节按键状态Bit 0: 左键按下(1)<br>Bit 1: 右键按下(1…...

【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】1.27 线性代数王国:矩阵分解实战指南
1.27 线性代数王国:矩阵分解实战指南 #mermaid-svg-JWrp2JAP9qkdS2A7 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-JWrp2JAP9qkdS2A7 .error-icon{fill:#552222;}#mermaid-svg-JWrp2JAP9qkdS2A7 .erro…...

Kafka常见问题之 java.io.IOException: Disk error when trying to write to log
文章目录 Kafka常见问题之 java.io.IOException: Disk error when trying to write to log1. 问题概述2. 问题排查方向(1)磁盘空间不足(2)磁盘 I/O 故障(3)Kafka 日志文件损坏(4)Kaf…...

libOnvif通过组播不能发现相机
使用libOnvif库OnvifDiscoveryClient类, auto discovery new OnvifDiscoveryClient(QUrl(“soap.udp://239.255.255.250:3702”), cb.Build()); 会有错误: end of file or no input: message transfer interrupted or timed out(30 sec max recv delay)…...
 :Table API SQL (一) 概览)
Flink (十二) :Table API SQL (一) 概览
Apache Flink 有两种关系型 API 来做流批统一处理:Table API 和 SQL。Table API 是用于 Scala 和 Java 语言的查询API,它可以用一种非常直观的方式来组合使用选取、过滤、join 等关系型算子。Flink SQL 是基于 Apache Calcite 来实现的标准 SQL。无论输入…...

FFmpeg(7.1版本)的基本组成
1. 前言 FFmpeg 是一个非常流行的开源项目,它提供了处理音频、视频以及其他多媒体内容的强大工具。FFmpeg 包含了大量的库,可以用来解码、编码、转码、处理和播放几乎所有类型的多媒体文件。它广泛用于视频和音频的录制、转换、流媒体传输等领域。 2. F…...

基于微信小程序的辅助教学系统的设计与实现
标题:基于微信小程序的辅助教学系统的设计与实现 内容:1.摘要 摘要:随着移动互联网的普及和微信小程序的兴起,基于微信小程序的辅助教学系统成为了教育领域的一个新的研究热点。本文旨在设计和实现一个基于微信小程序的辅助教学系统,以提高教…...

单片机基础模块学习——超声波传感器
一、超声波原理 左边发射超声波信号,右边接收超声波信号 左边的芯片用来处理超声波发射信号,中间的芯片用来处理接收的超声波信号 二、超声波原理图 T——transmit 发送R——Recieve 接收 U18芯片对输入的N_A1信号进行放大,然后输入给超声…...

HTML<hgroup>标签
例子: 使用hgroup元素标记标题和段落是相关的: <hgroup> <h2>Norway</h2> <p>The land with the midnight sun.</p> </hgroup> 定义和用法: 标签<hgroup>用于包围标题和一个或多个<p&g…...

C++并发编程指南08
以下是经过优化排版后的5.3节内容,详细解释了C中的同步操作和强制排序机制。每个部分都有详细的注释和结构化展示。 文章目录 5.3 同步操作和强制排序假设场景示例代码 5.3.1 同步发生 (Synchronizes-with)基本思想 5.3.2 先行发生 (Happens-before)单线程环境多线程…...
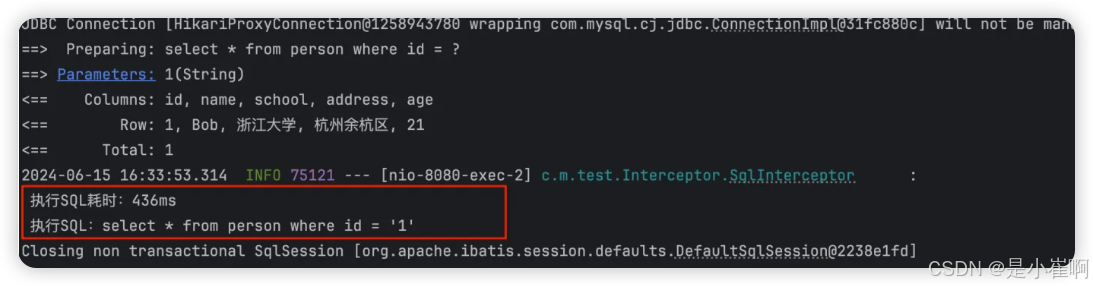
Spring Boot - 数据库集成03 - 集成Mybatis
Spring boot集成Mybatis 文章目录 Spring boot集成Mybatis一:基础知识1:什么是MyBatis2:为什么说MyBatis是半自动ORM3:MyBatis栈技术演进3.1:JDBC,自行封装JDBCUtil3.2:IBatis3.3:My…...

python:洛伦兹变换
洛伦兹变换(Lorentz transformations)是相对论中的一个重要概念,特别是在讨论时空的变换时非常重要。在四维时空的背景下,洛伦兹变换描述了在不同惯性参考系之间如何变换时间和空间坐标。在狭义相对论中,洛伦兹变换通常…...

“星门计划对AI未来的意义——以及谁将掌控它”
“星门计划对AI未来的意义——以及谁将掌控它” 图片由DALL-E 3生成 就在几天前,唐纳德特朗普宣布了“星门计划”,OpenAI随即跟进,分享了更多细节。他们明确表示,计划在未来四年内投资5000亿美元,在美国为OpenAI构建一…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
