outlook邮箱pc/mac客户端下载 含最新版
新的 Outlook for Windows or mac 为 Outlook 应用带来了最新功能、智能辅助功能和新的新式简化设计。 你可以根据自己的风格定制它,并使用新的 Outlook for Windows/mac 执行更多操作!

览版,与我们一起开始旅程,并帮助我们塑造新的 Outlook for Windows /mac的未来。
重要: 新的 Outlook for Windows 支持 Exchange 支持的 Microsoft 365 工作或学校帐户、Outlook.com 帐户和 Gmail。 目前,新的 Outlook for Windows 不支持其他帐户类型,如 Yahoo!、iCloud 或其他通过 POP/IMAP 协议连接的帐户类型。 新的 Outlook for Windows 目前也不支持本地、混合或主权 Exchange 部署。
 outlook2021下载
outlook2021下载

1、下载后解压出来,【重要】:不要直接在压缩包里打开文件;
2、等待安装进度

3、完了之后关闭弹窗即可;

4、在开始菜单中找到outlook

5、或者直接搜索O字母;
6、在这里也可以找到outlook选项;
7、然后双击outlook
8、登录你的outlook邮箱类型;
相关文章:

outlook邮箱pc/mac客户端下载 含最新版
新的 Outlook for Windows or mac 为 Outlook 应用带来了最新功能、智能辅助功能和新的新式简化设计。 你可以根据自己的风格定制它,并使用新的 Outlook for Windows/mac 执行更多操作! 览版,与我们一起开始旅程,并帮助我们塑造新…...

缓存雪崩、缓存穿透、缓存击穿分别是什么?如何解决?
缓存中存放的大多都是热点数据,目的就是从缓存中获取数据,而不用直接访问数据库,从而提高查询效率 缓存雪崩 概念 指缓存在同一时间大面积失效,后面的请求直接访问数据库,导致数据库短时间内压力过大而崩溃ÿ…...

VBA实战篇学习笔记02 Err错误处理
文章目录 专题VI 错误处理课时38 常见错误类型错误代码13 :类型不匹配错误代码91: 对象变量或者with变量未设置错误代码1004: 视具体错误类型而变化 课时39 Err错误处理On Error Resume Next :Resume语句:Resume Next语句:未知错误:Exit SubOn Error Goto 0 专题VI 错误处理 课…...

【Git】拉取代码/提交代码
1.从将本地代码放入远程仓库 (如果有分支的情况) [git checkout xx切换分支后 git add . 将本地所有改动文件新增 commit之后 git push(将代码全部提交)] 分支操作 #查看分支 git branch #创建分支 git branch test #切换分支 git checkout test #修改代码 #提交代码git ad…...
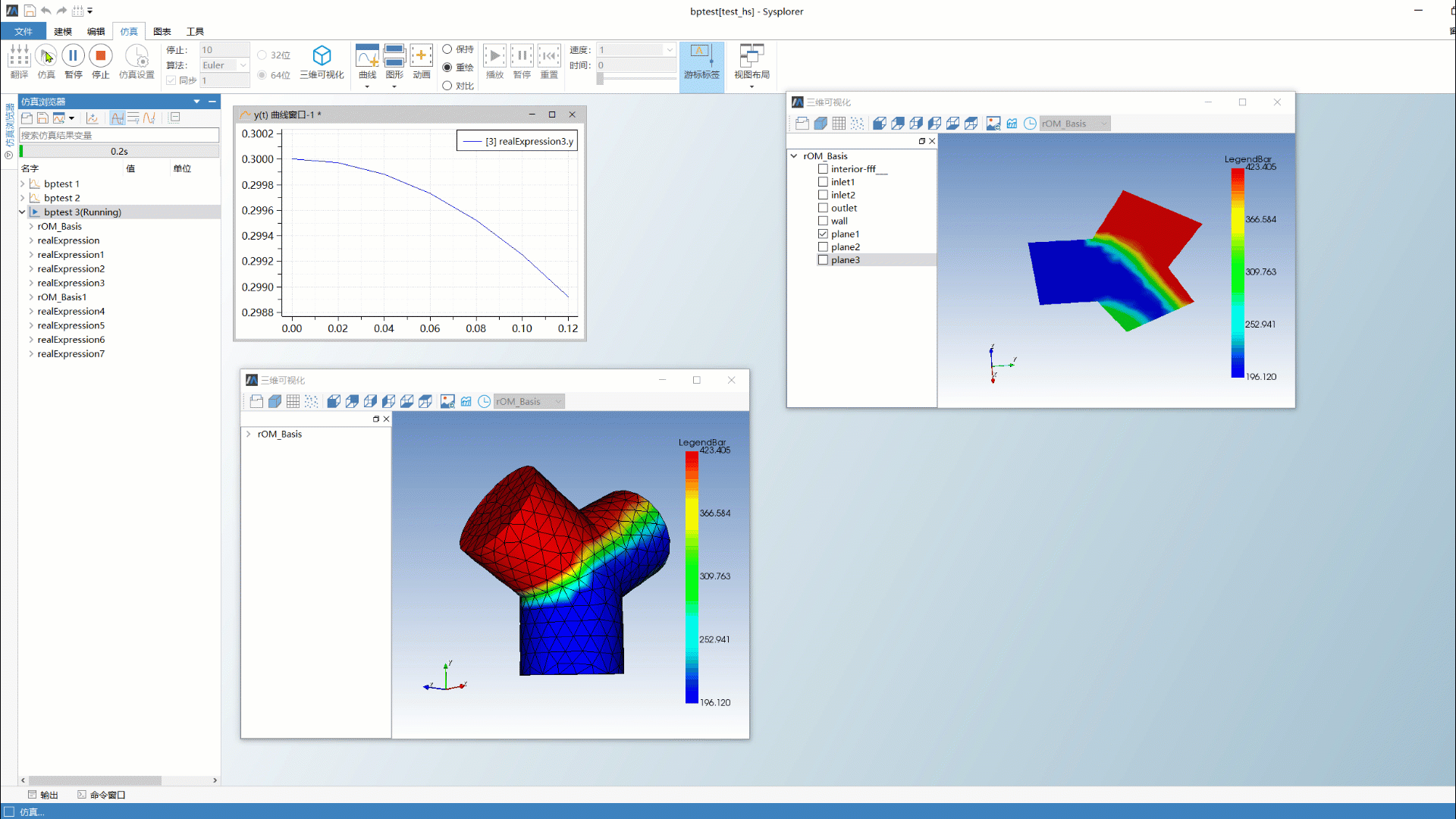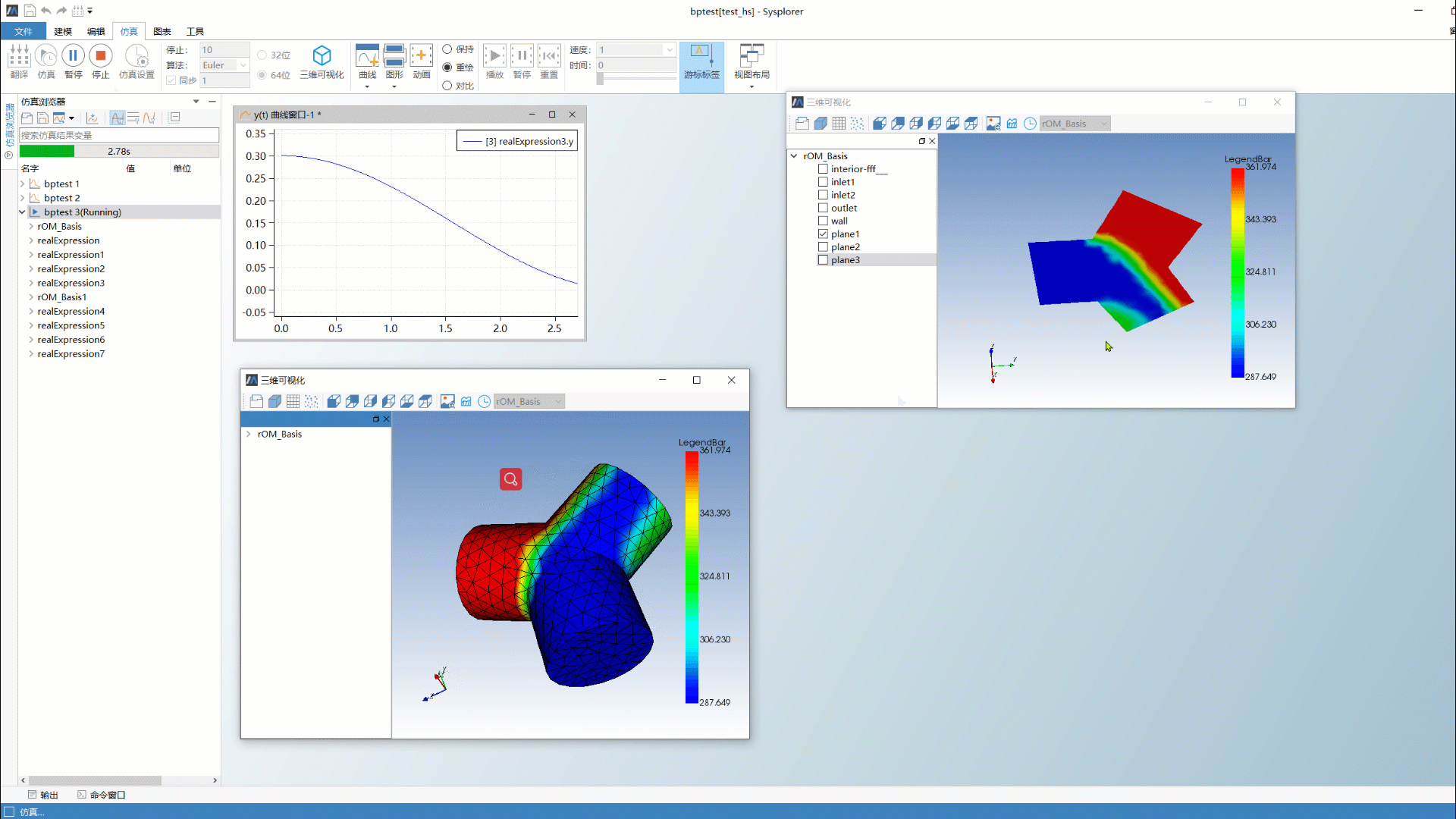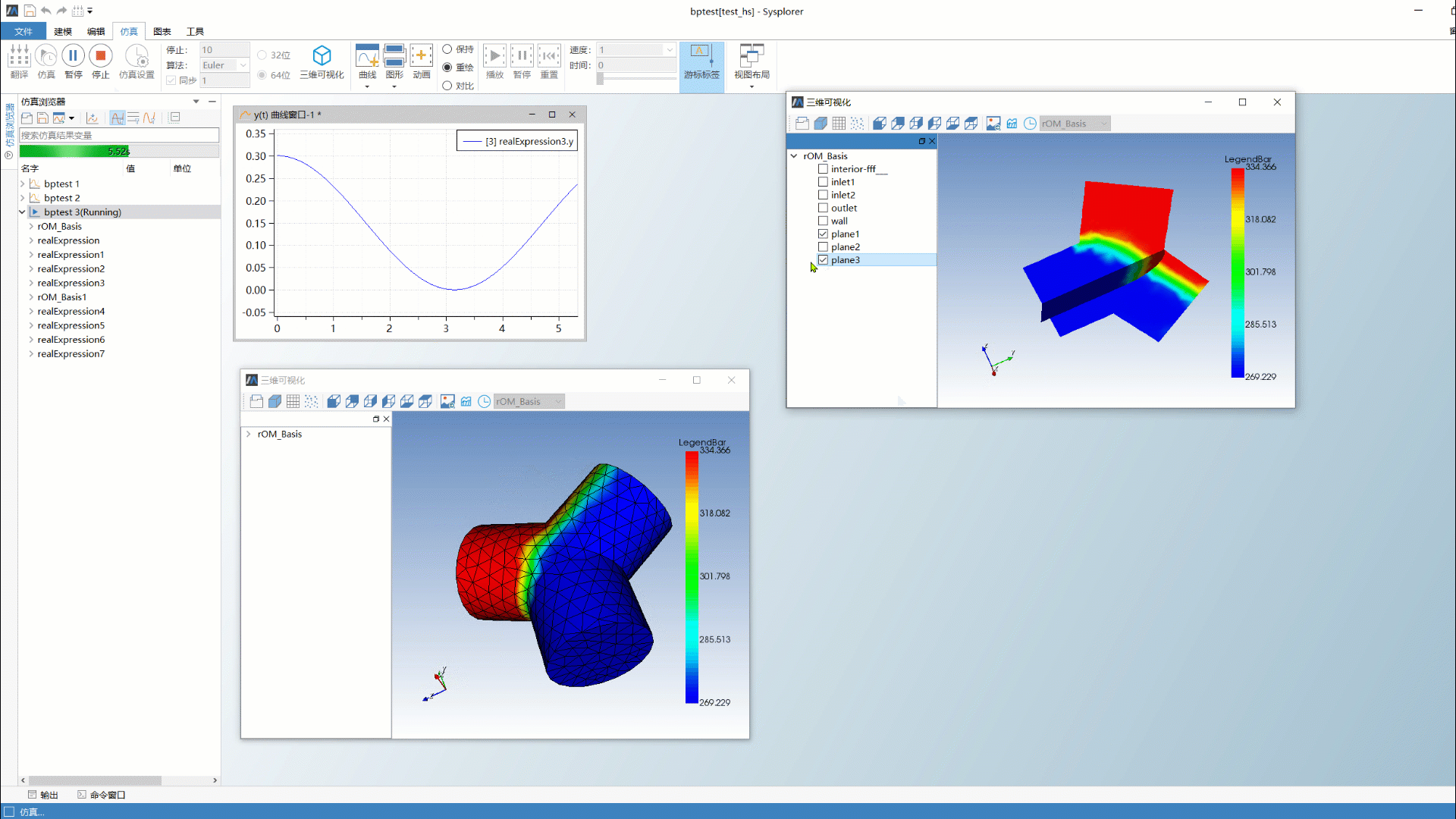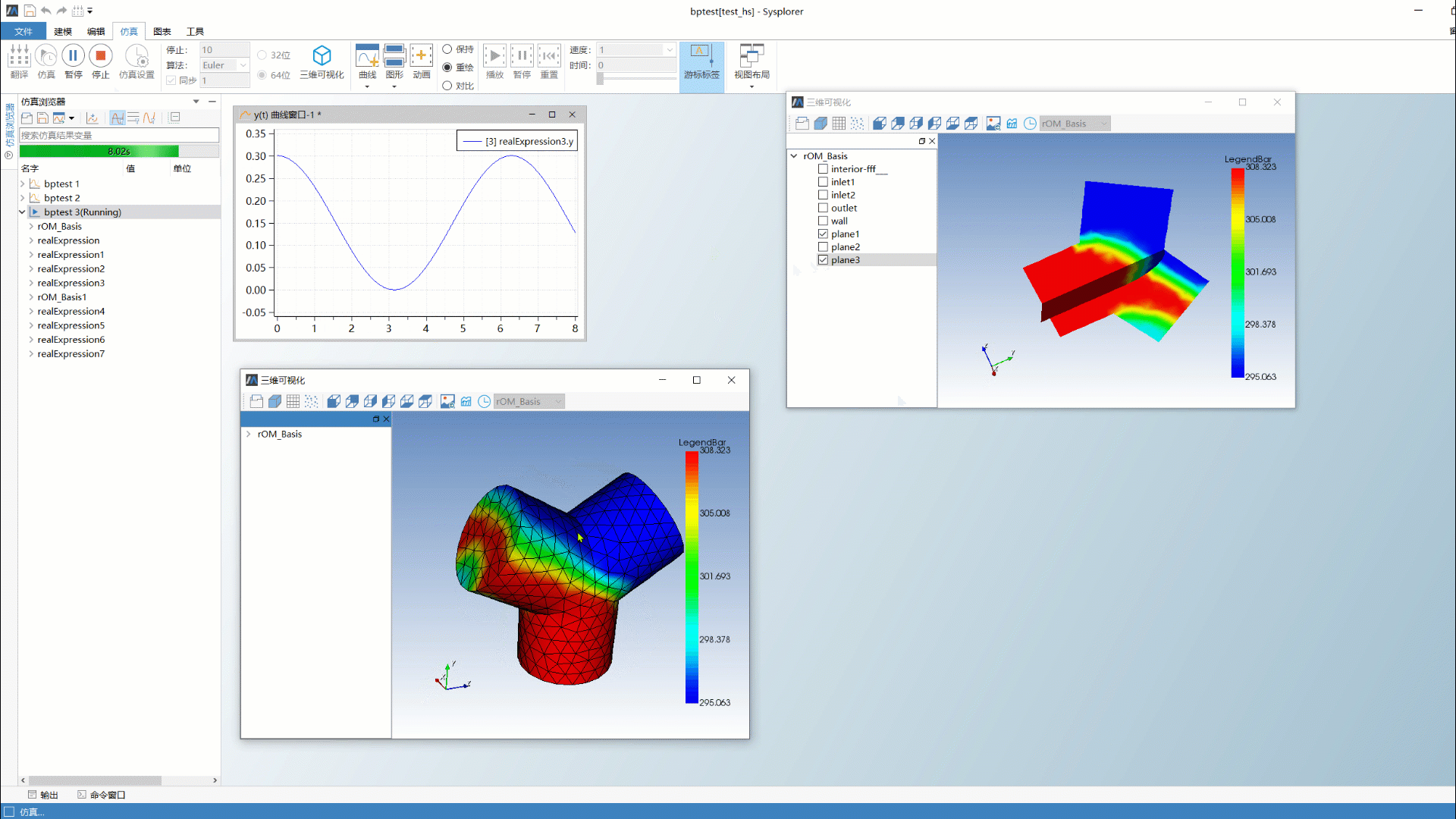
产品预览 | 系统仿真与三维专业场仿真融合——MWORKS模型降阶工具箱
1 引言 近二十年来,数字化技术迅猛发展,以美国和中国提出装备数字工程为标志,人类迈入全新的数字化时代。装备数字化需要对装备的运行状态和行为进行准确的模拟和预测,这就需要利用系统仿真技术。系统仿真技术能够综合考虑装备的…...

我们都遇到过的这些ajax代码到底什么意思?
hello,我是小索奇,本篇文章给大家带来ajax中常用的一些代码,为什么写这些呢? 因为小索奇也看黑马、尚硅谷等老师的视频,在学习java的时候经常会介绍ajax,导致很多不了解的伙伴一脸懵然,以防万一…...

TiDB实战篇-TiCDC
目录 简介 原理 使用场景 使用限制 硬件配置 部署 在安装TiDB的时候部署 扩容部署 操作 管理CDC 管理工具 查看状态 创建同步任务 公共参数 CDC任务同步到MySQL实战 同步命令 查看所有的同步任务 同步任务的状态 管理同步任务 查看一个同步信息的具体情况 …...

ElasticSearch第十七讲 ES索引别名的使用
索引别名 ES中可以为索引添加别名,一个别名可以指向到多个索引中,同时在添加别名时可以设置筛选条件,指向一个索引的部分数据,实现在关系数据库汇总的视图功能,这就是ES中别名的强大之处。别名是一个非常实用的功能,为我们使用索引提供了极大的灵活性,许多ES的API都支持…...
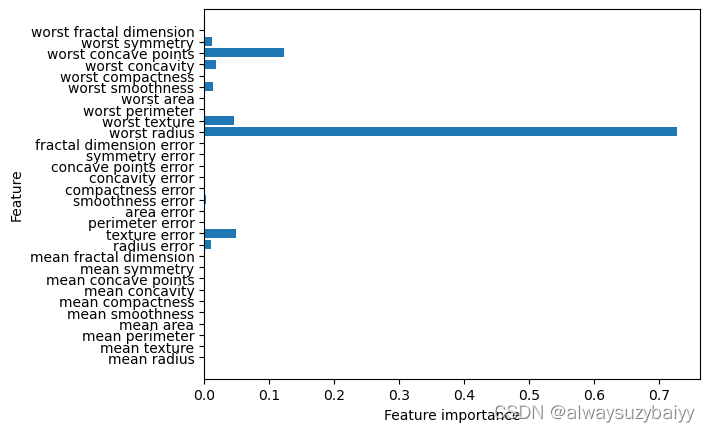
第二个机器学习应用:乳腺癌数据集在决策树模型上的挖掘
目录 决策树优化与可视化 1 决策树分类 2 决策树可视化 3 显示树的特征重要性 特征重要性可视化 决策树回归 1 决策树回归 决策树优化与可视化 1 决策树分类 from sklearn.datasets import load_breast_cancer from sklearn.tree import DecisionTreeClassifier from sk…...
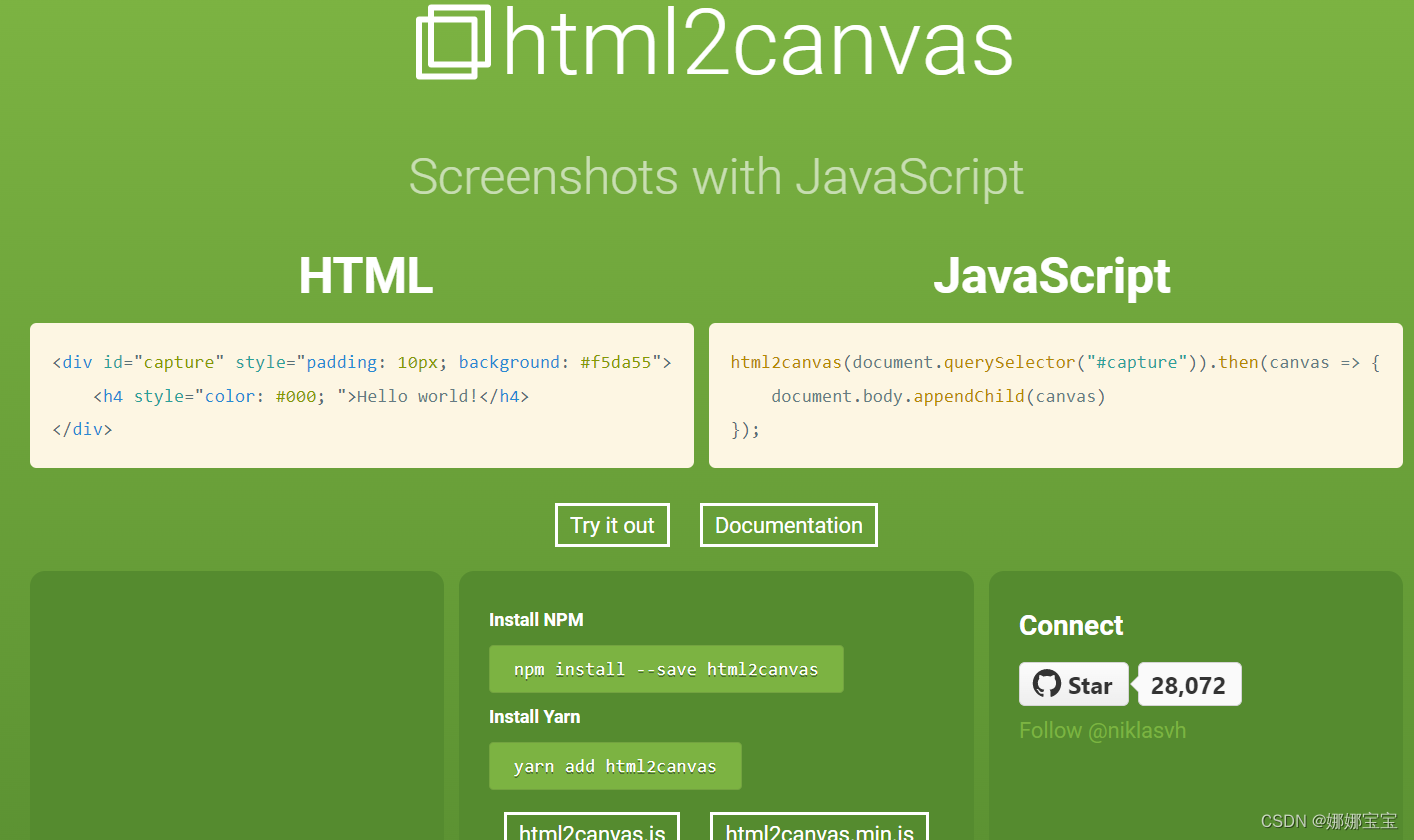
前端canvas截图酷游地址的方法!
前情提要 想在在JavaScript中,酷游专员KW9㍠ㄇEㄒ提供用HTML5的Canvas元素来剪取画面并存成SVG或PNG。 程式写法(一) 首先,需要在HTML中创建一个Canvas元素<canvas id"myCanvas"></canvas> 在JavaScript中,使用canv…...

2018年入学,2021年入职
2018年的春天,凌晨紧张地查着考研成绩,运气好,384,远远超出了我的预期“能进复试就行”,秉承着“尽人事,知天命”的格言,坚持复习完,坚持到考试最后一秒。 在考试之前,我…...
python+nodejs+ssm+vue 基于协同过滤的旅游推荐系统
本文首先介绍了旅游推荐的发展背景与发展现状,然后遵循软件常规开发流程,首先针对系统选取适用的语言和开发平台,根据需求分析制定模块并设计数据库结构,再根据系统总体功能模块的设计绘制系统的功能模块图,流程图以及…...
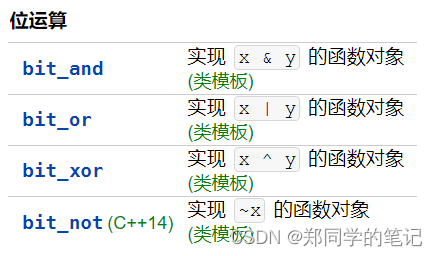
【STL十四】函数对象(function object)_仿函数(functor)——lambda表达式
【STL十四】函数对象(function object)_仿函数(functor)——lambda表达式 一、函数对象(function object)二、函数对象优点三、分类四、头文件五、用户定义函数对象demo六、std::内建函数对象1、 算术运算函…...

如何写出高质量的前端代码
写出高质量的前端代码是每个前端开发人员的追求。在一个复杂的项目中,代码质量对于项目的可维护性、可扩展性和可读性都有很大的影响。本文将介绍一些如何写出高质量前端代码的技巧和最佳实践。 一、注重代码结构和组织 1.1 遵循一致的命名规范 命名规范是编写高…...

YOLOv7如何提高目标检测的速度和精度,基于优化算法提高目标检测速度
目录 一、学习率调度二、权重衰减和正则化三、梯度累积和分布式训练1、梯度累积2、分布式训练 四、自适应梯度裁剪 大家好,我是哪吒。 上一篇介绍了YOLOv7如何提高目标检测的速度和精度,基于模型结构提高目标检测速度,本篇介绍一下基于优化算…...

CentOS 7中安装配置Nginx的教程指南
1. 安装Nginx 在终端中执行以下命令以安装Nginx: sudo yum install epel-release sudo yum install nginx安装完成后的 Nginx 内容通常会被安装在以下目录下: /etc/nginx: 该目录包含 Nginx 的配置文件,包括 nginx.conf 和 conf.d 目录下的…...

Vicuna- 一个类 ChatGPT开源 模型
Meta 开源 LLaMA(大羊驼)系列模型为起点,研究人员逐渐研发出基于LLaMA的Alpaca(羊驼)、Alpaca-Lora、Luotuo(骆驼)等轻量级类 ChatGPT 模型并开源。 google提出了一个新的模型:Vicuna(小羊驼)。该模型基于LLaMA,参数量13B。Vicuna-13B 通过微调 LLaMA 实现了高性能…...

5.1 数值微分
学习目标: 作为数值分析的基础内容,我建议你可以采取以下步骤来学习数值微分: 掌握微积分基础:数值微分是微积分中的一个分支,需要先掌握微积分基础知识,包括导数、极限、微分等。 学习数值微分的概念和方…...
云计算服务安全评估办法
云计算服务安全评估办法 2019-07-22 14:46 来源: 网信办网站【字体:大 中 小】打印 国家互联网信息办公室 国家发展和改革委员会 工业和信息化部 财政部关于发布《云计算服务安全评估办法》的公告 2019年 第2号 为提高党政机关、关键信息基础设施运营者…...
laravel5.6.* + vue2 创建后台
本地已经安装好了composer 1.新建 Laravel5.6.*项目 composer create-project --prefer-dist laravel/laravel laravel5vue2demo 5.6.* 2. cd laravel5vue2demo 3. npm install /routes/web.php 路由文件中, 修改 Route::get(/, function () {return view(index); });新建…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...
