安装gitea
1、安装包（gitea-1.13.1-linux-amd64）上传到服务器，并添加执行权限
链接：https://pan.baidu.com/s/1SAxko0RhVmmD21Ev_m5JFg
提取码：ft07
chmod +x gitea-1.13.1-linux-amd64
2、执行 ./gitea-1.13.1-linux-amd64 web，默认使用 3000 端口，防火墙允许：iptables -I INPUT -p tcp --dport 3000 -j ACCEPT
3、浏览器打开然后在界面进行相关配置
4、也可以在 gitea 的运行目录下的 custom/conf/app.ini 文件进行配置
5、方便启动，可以建立软连接(路径根据个人的更改一下喔) ln -s /software/gitea/gitea-1.13.1-linux-amd64 /usr/local/bin/gitea
6、后台启动：
nohup gitea web > gitea.log 2>&1 &
| nohup | 后台运行 |
| > gitea.log | 重定向到 gitea.log 文件 |
| 2>&1 | 标准错误2 重定向到标准输出&1 |
| & | 终端退出，不关闭程序 |
相关文章：
安装gitea
1、安装包（gitea-1.13.1-linux-amd64）上传到服务器，并添加执行权限 链接：https://pan.baidu.com/s/1SAxko0RhVmmD21Ev_m5JFg 提取码：ft07 chmod x gitea-1.13.1-linux-amd64 2、执行 ./gitea-1.13.1-linux-amd64 web…...
Java异常处理传递规范总结
java 异常分类 Thorwable类（表示可抛出）是所有异常和错误的超类，两个直接子类为Error和Exception，分别表示错误和异常。其中异常类Exception又分为运行时异常(RuntimeException)和非运行时异常， 这两种异常有很大的区别…...
2d俯视视角游戏，可以切换多种枪械
文章目录 一、 介绍二、 人物移动、鼠标控制转向三、子弹脚本四、子弹随机抛壳五、 爆炸特效六、 发射子弹七、 子弹、弹壳对象池八、 散弹枪九、 火箭弹、发射火箭十、 下载工程文件 一、 介绍 2d俯视视角游戏。 人物视角跟随鼠标移动 多种枪械 抛壳效果 多种设计效果 对象池…...
大四的告诫
保研/考研方向就绩点，（各种）比赛，（考研）刷题为主 工作就算法（比赛），项目，实习为主 👂 LOCK OUT - $atori Zoom/KALONO - 单曲 - 网易云音乐 &…...
滚珠螺杆在设备上的应用
滚珠螺杆跟直线导轨一样，是很多机械设备上不可或缺的重要部件，它是确保机器能够具备高加工精度的前提条件，因此本身对于精度的要求也相当地高。今天，我们就来了解一下滚珠螺杆在不同设备上的应用吧！ 1、大型的加工中心…...
Day41线程同步
线程同步 案例：三个窗口卖100张票 //定义一个类SellTicket实现Runnable接口，定义成员变量100张票 public class SellTicket implements Runnable{private int tickets 100;//重写run方法Overridepublic void run(){while (true){ //没有票后&…...
设计模式之享元模式
参考资料 曾探《JavaScript设计模式与开发实践》；「设计模式 JavaScript 描述」享元模式设计模式之享元模式Javascript 设计模式 - 享元模式 定义 享元模式的英文叫：Flyweight Design Pattern。享元设计模式是用于性能优化的模式，这种设计…...
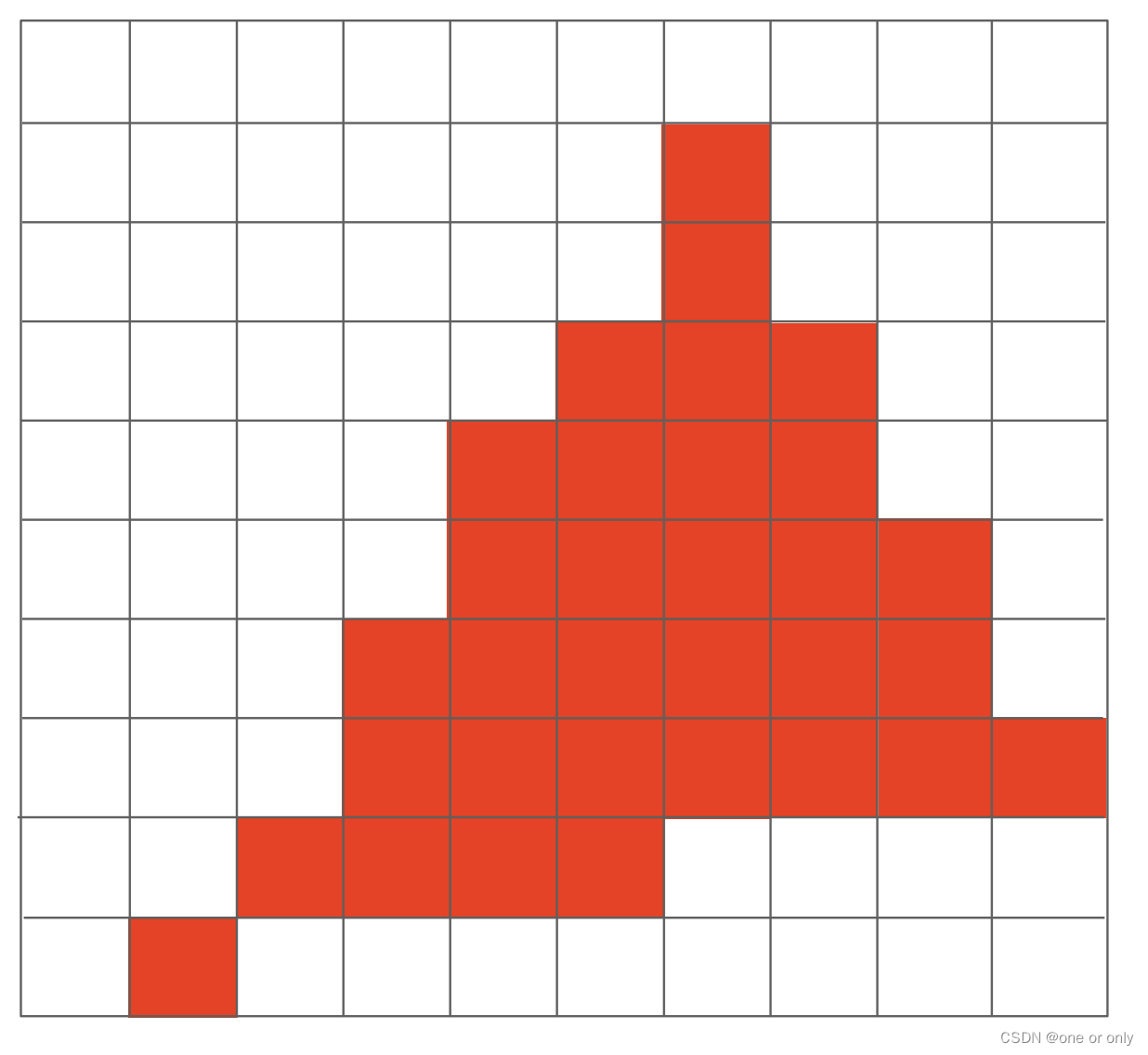
【GAMES101】05 Rasterization（Triangles）
光栅化过程：将一系列变换后的三角形转换为像素的过程。 三角形在图形学中得到很多的应用。 最基础的多边形（边数最少）。任何多边形都可以拆成三角形。性质：三角形内部一定是平面的。三角形内外部定义非常清楚。定义三个顶点后&a…...
13. Pod 从入门到深入理解（二）
本章讲解知识点 Pod 容器共享 VolumeConfigMapSecretDownward APIEmptyDir VolumeHostPath Volume1. Pod 容器共享 Volume 1.1. Volume 的背景及需要解决的问题 存储是必不可少的，对于服务运行产生的日志、数据，必须有一个地方进行保存，但是我们的容器每一次重启都是“恢复…...
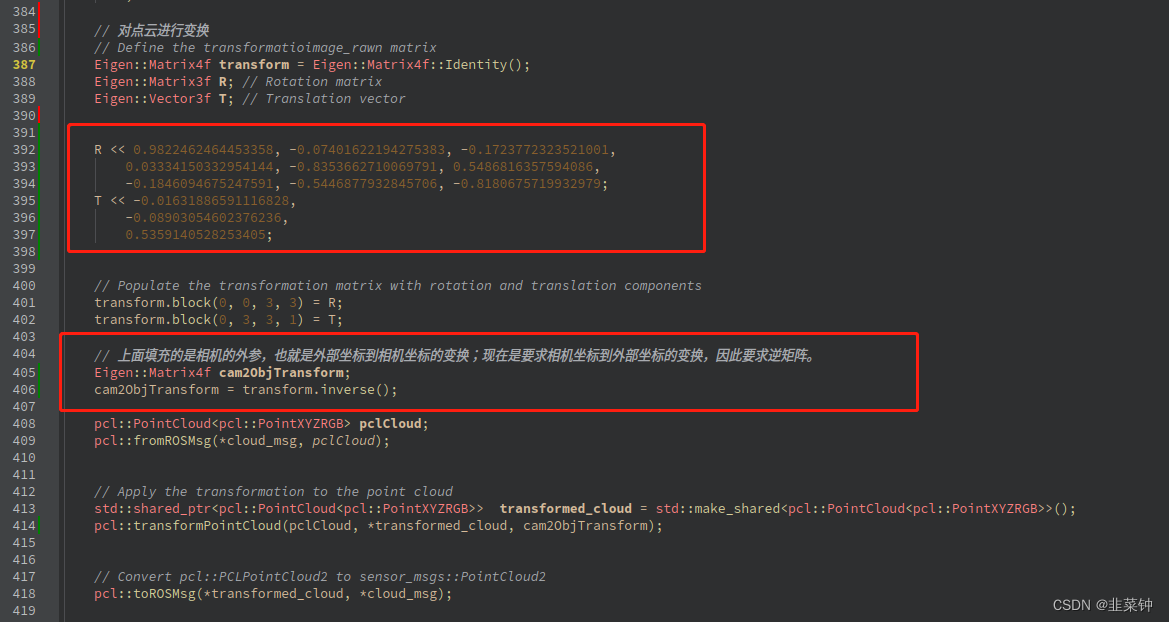
ORBBEC（奥比中光）AstraPro相机在ROS2下的标定与D2C（标定与配准）
文章目录 1.rgb、depth相机标定矫正1.1.标定rgb相机1.2.标定depth相机1.3.rgb、depth相机一起标定（效果重复了，但是推荐使用）1.4.取得标定结果1.4.1.得到的标定结果的意义 1.5.IR、RGB相机分别应用标定结果1.5.1.openCV应用标定结果1.5.2.ros…...
常量与变量：编程中重要的两种数据类型
常量与变量 在编程中，我们常常需要存储一些数据。这些数据有些是恒定不变的，有些却是可以随时变化的。对于恒定不变的数据，我们称之为常量；对于可以变化的数据，我们则称之为变量。这两种数据类型在程序中非常重要&…...
( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数 难度：中等 给定一个包含 n 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。 假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。 你…...
【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...
武忠祥老师每日一题||定积分基础训练（三）
常用的基本不等式： sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...
Docker安装常用软件-Apollo（有问题）
零：apollo概念介绍 官网网站：GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址：mirrors / ctripcorp / apollo GitCode …...
f(x)与|f(x)|，f ‘ (x)，F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. （因为f(x)在x0的连续点>x0必为|f(x)|的连续点） 注：”[a,b]连续“包括&#…...
今天面了一个来字节要求月薪23K，明显感觉他背了很多面试题...
最近有朋友去字节面试，面试前后进行了20天左右，包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说，80%的人都会栽在第一轮面试，要不是他面试前做足准备，估计都坚持不完后面几轮面试。 其实&…...
如何使用二元三次回归分析建立预测模型？（分析、原理、代码示例）
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型，常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型，其中包括两个自变量（通常…...
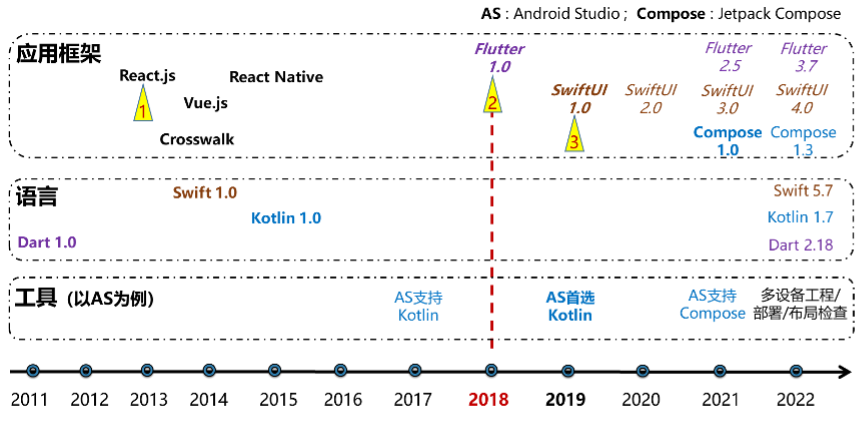
面向万物智联的应用框架的思考和探索（上）
原文：面向万物智联的应用框架的思考和探索（上），点击链接查看更多技术内容。 应用框架，是操作系统连接开发者生态，实现用户体验的关键基础设施。其中，开发效率和运行体验是永恒的诉求，…...
《Python机器学习基础教程》第1章学习笔记
目录 第1章 引言 1.1 为何选择机器学习 1.1.1 机器学习能够解决的问题 第1章 引言 机器学习又称为预测分析或统计学习，是一个交叉学科，是从数据中提取知识。 1.1 为何选择机器学习 智能应用早期，使用专家设计的规则体系来设计。 缺点&…...
linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源（HTML/CSS/图片等），响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址，提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
iOS 26 携众系统重磅更新，但“苹果智能”仍与国行无缘
美国西海岸的夏天，再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至，这不仅是开发者的盛宴，更是全球数亿苹果用户翘首以盼的科技春晚。今年，苹果依旧为我们带来了全家桶式的系统更新，包括 iOS 26、iPadOS 26…...
FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下，无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作，还是游戏直播的画面实时传输，低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架，凭借其灵活的编解码、数据…...
【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角，以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向，距离坐标原点x个像素;第二个是y坐标，表示当前位置为垂直方向，距离坐标原点y个像素。 坐标体系-像素 …...
算法笔记2
1.字符串拼接最好用StringBuilder，不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术：基于互相关的相干体技术（Correlation）第二代相干体技术：基于相似的相干体技术（Semblance）基于多道相似的相干体…...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...
站群服务器的应用场景都有哪些？
站群服务器主要是为了多个网站的托管和管理所设计的，可以通过集中管理和高效资源的分配，来支持多个独立的网站同时运行，让每一个网站都可以分配到独立的IP地址，避免出现IP关联的风险，用户还可以通过控制面板进行管理功…...
MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 ：主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 ：确保数据的完整性，便于数据的查询和管理。 示例 ：在学生信息表中，学号可以作为主键ÿ…...
android13 app的触摸问题定位分析流程
一、知识点 一般来说，触摸问题都是app层面出问题，我们可以在ViewRootImpl.java添加log的方式定位；如果是touchableRegion的计算问题，就会相对比较麻烦了，需要通过adb shell dumpsys input > input.log指令，且通过打印堆栈的方式，逐步定位问题，并找到修改方案。 问题…...