Scalable Vector Graphics (SVG)中的svg、clipPath、mask元素
Scalable Vector Graphics (SVG)是一种用于描述二维向量图形的XML基础标记语言。使用SVG可以实现丰富的图形效果,而不需要像使用位图那样考虑分辨率和像素密度的问题,可以在不同设备上展示出相同的高质量图像。
在SVG中,除了基本形状如circle、rect、line等,还有一些特殊的元素可以实现更加复杂的效果。本文将介绍SVG中的svg、clipPath、mask元素的用法和效果。
svg元素
首先,我们来看一下svg元素。在SVG中,所有的图形都必须包含在svg元素中。svg元素是画布,在其中定义的图形可以在其中展示出来。我们可以设置svg元素的宽度和高度来限制其内部的图形尺寸。下面是一个简单的例子:
<svg width="200" height="200"> <rect x="50" y="50" width="100" height="100" fill="red"/> </svg>在这个例子中,我们设置了一个200x200像素的svg元素,并在其中定义了一个红色的正方形。其中,x和y表示位置,width和height表示宽度和高度。可以通过改变这些属性来修改正方形的位置和尺寸。
除了宽度和高度,svg元素还可以设置其他属性,比如fill和stroke。fill表示填充颜色,stroke表示描边颜色。我们还可以设置不同的形状、样式等来实现更加复杂的效果。以下是一些常见的SVG元素:
- rect - 矩形
- circle - 圆形
- ellipse - 椭圆形
- line - 直线
- path - 路径
除了这些基本形状,我们还可以使用SVG滤镜、模糊效果等来进一步美化图像。
clipPath元素
接下来,我们来介绍clipPath元素。clipPath元素用于定义剪切路径,可以将图形裁剪成我们想要的形状。剪切路径可以是SVG元素中的任何形状,也可以是使用path元素定义的自定义路径。以下是一个简单的例子:
<svg width="200" height="200"> <clipPath id="myClip"> <circle cx="100" cy="100" r="50"/> </clipPath> <rect x="0" y="0" width="200" height="200" fill="red" clip-path="url(#myClip)"/> </svg>在这个例子中,我们定义了一个半径为50像素、圆心坐标为(100,100)的圆形剪切路径,并将其id设置为myClip。然后,我们定义了一个红色的矩形,并将其裁剪成了myClip中定义的圆形形状,通过clip-path属性引用myClip元素。
mask元素
最后,我们来介绍mask元素。mask元素用于定义蒙版,可以控制图像的透明度和可见性,使得只有在指定区域内的图像才会显示出来。蒙版可以是SVG元素中的任何形状,也可以是使用path元素定义的自定义路径。以下是一个简单的例子:
<svg width="200" height="200"> <mask id="myMask"> <rect x="0" y="0" width="200" height="200" fill="white"/> <circle cx="100" cy="100" r="50" fill="black"/> </mask> <rect x="50" y="50" width="100" height="100" fill="red" mask="url(#myMask)"/> </svg>在这个例子中,我们定义了一个id为myMask的蒙版,其中包含了一个白色的矩形和一个半径为50像素、圆心坐标为(100,100)的黑色圆形。然后,我们定义了一个红色的正方形,并将其应用到myMask蒙版中,使得只有在黑色圆形区域内的图像才会显示出来。
总结
在SVG中,svg、clipPath、mask元素都是非常有用的元素,可以帮助我们实现各种不同的图形效果。svg元素是画布,在其中定义的图形可以在其中展示出来;clipPath元素用于定义剪切路径,可以将图形裁剪成我们想要的形状;mask元素用于定义蒙版,可以控制图像的透明度和可见性。使用这些元素,可以实现各种各样的丰富的图形效果,并让SVG更加
相关文章:
中的svg、clipPath、mask元素)
Scalable Vector Graphics (SVG)中的svg、clipPath、mask元素
Scalable Vector Graphics (SVG)是一种用于描述二维向量图形的XML基础标记语言。使用SVG可以实现丰富的图形效果,而不需要像使用位图那样考虑分辨率和像素密度的问题,可以在不同设备上展示出相同的高质量图像。 在SVG中,除了基本形状如circl…...
Java基础(十五)集合框架
1. 集合框架概述 1.1 生活中的容器 1.2 数组的特点与弊端 一方面,面向对象语言对事物的体现都是以对象的形式,为了方便对多个对象的操作,就要对对象进行存储。另一方面,使用数组存储对象方面具有一些弊端,而Java 集合…...

安装gitea
1、安装包(gitea-1.13.1-linux-amd64)上传到服务器,并添加执行权限 链接:https://pan.baidu.com/s/1SAxko0RhVmmD21Ev_m5JFg 提取码:ft07 chmod x gitea-1.13.1-linux-amd64 2、执行 ./gitea-1.13.1-linux-amd64 web…...

Java异常处理传递规范总结
java 异常分类 Thorwable类(表示可抛出)是所有异常和错误的超类,两个直接子类为Error和Exception,分别表示错误和异常。其中异常类Exception又分为运行时异常(RuntimeException)和非运行时异常, 这两种异常有很大的区别…...
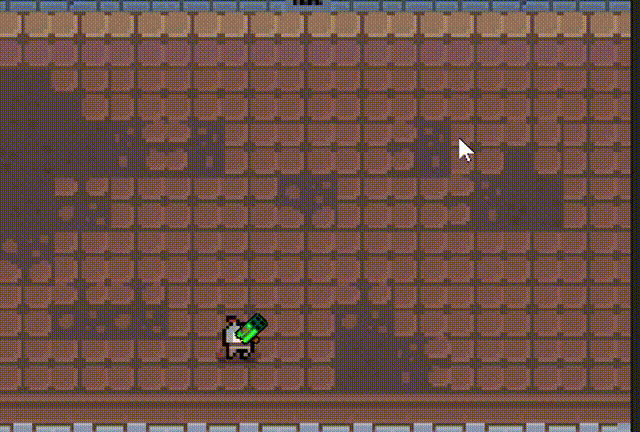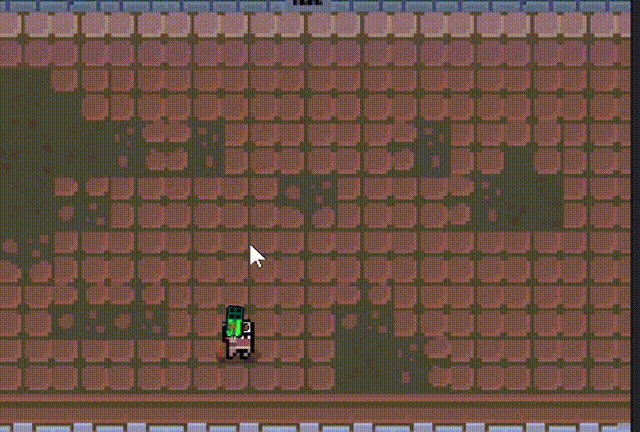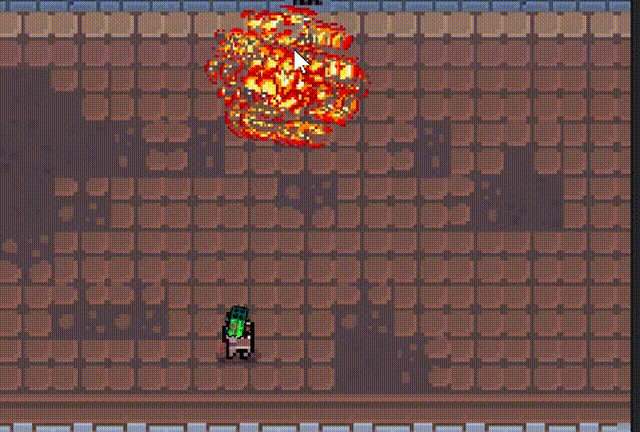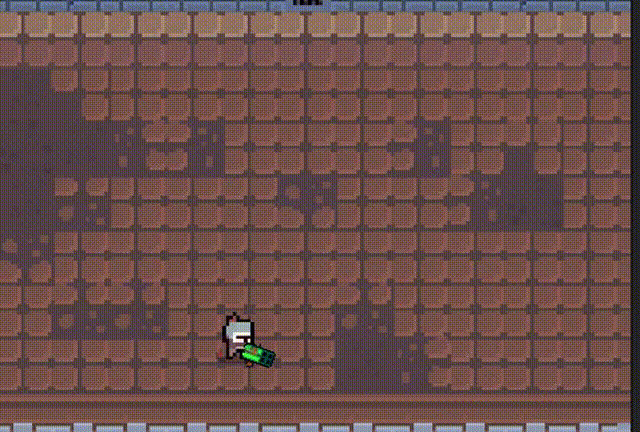
2d俯视视角游戏,可以切换多种枪械
文章目录 一、 介绍二、 人物移动、鼠标控制转向三、子弹脚本四、子弹随机抛壳五、 爆炸特效六、 发射子弹七、 子弹、弹壳对象池八、 散弹枪九、 火箭弹、发射火箭十、 下载工程文件 一、 介绍 2d俯视视角游戏。 人物视角跟随鼠标移动 多种枪械 抛壳效果 多种设计效果 对象池…...
大四的告诫
保研/考研方向就绩点,(各种)比赛,(考研)刷题为主 工作就算法(比赛),项目,实习为主 👂 LOCK OUT - $atori Zoom/KALONO - 单曲 - 网易云音乐 &…...

滚珠螺杆在设备上的应用
滚珠螺杆跟直线导轨一样,是很多机械设备上不可或缺的重要部件,它是确保机器能够具备高加工精度的前提条件,因此本身对于精度的要求也相当地高。今天,我们就来了解一下滚珠螺杆在不同设备上的应用吧! 1、大型的加工中心…...

Day41线程同步
线程同步 案例:三个窗口卖100张票 //定义一个类SellTicket实现Runnable接口,定义成员变量100张票 public class SellTicket implements Runnable{private int tickets 100;//重写run方法Overridepublic void run(){while (true){ //没有票后&…...

设计模式之享元模式
参考资料 曾探《JavaScript设计模式与开发实践》;「设计模式 JavaScript 描述」享元模式设计模式之享元模式Javascript 设计模式 - 享元模式 定义 享元模式的英文叫:Flyweight Design Pattern。享元设计模式是用于性能优化的模式,这种设计…...
【GAMES101】05 Rasterization(Triangles)
光栅化过程:将一系列变换后的三角形转换为像素的过程。 三角形在图形学中得到很多的应用。 最基础的多边形(边数最少)。任何多边形都可以拆成三角形。性质:三角形内部一定是平面的。三角形内外部定义非常清楚。定义三个顶点后&a…...
)
13. Pod 从入门到深入理解(二)
本章讲解知识点 Pod 容器共享 VolumeConfigMapSecretDownward APIEmptyDir VolumeHostPath Volume1. Pod 容器共享 Volume 1.1. Volume 的背景及需要解决的问题 存储是必不可少的,对于服务运行产生的日志、数据,必须有一个地方进行保存,但是我们的容器每一次重启都是“恢复…...
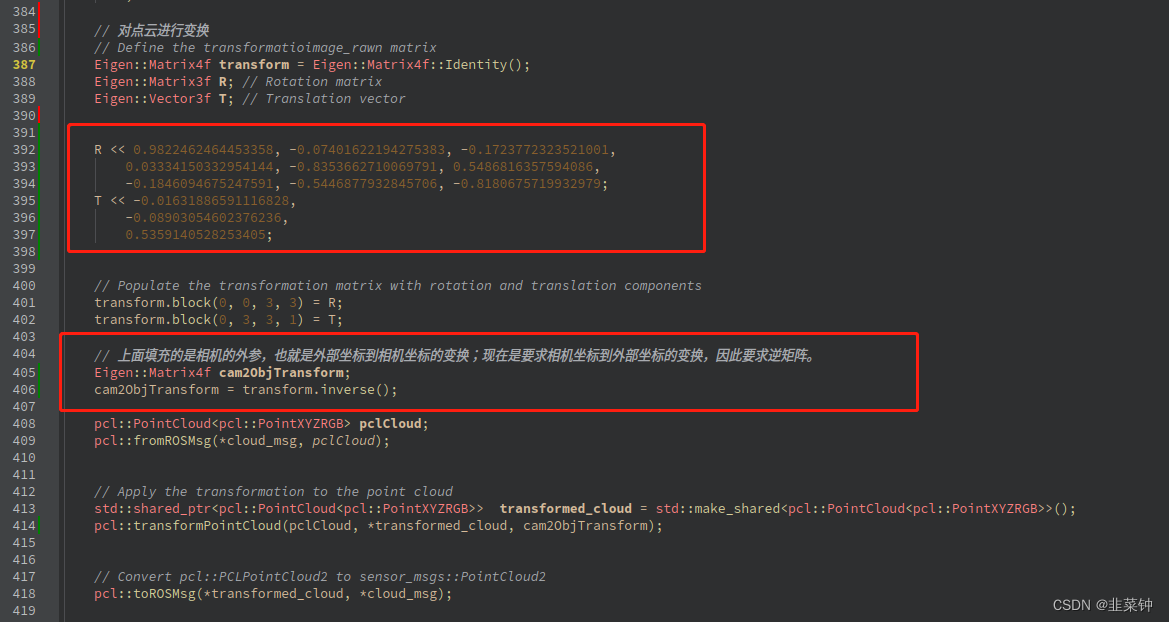
ORBBEC(奥比中光)AstraPro相机在ROS2下的标定与D2C(标定与配准)
文章目录 1.rgb、depth相机标定矫正1.1.标定rgb相机1.2.标定depth相机1.3.rgb、depth相机一起标定(效果重复了,但是推荐使用)1.4.取得标定结果1.4.1.得到的标定结果的意义 1.5.IR、RGB相机分别应用标定结果1.5.1.openCV应用标定结果1.5.2.ros…...

常量与变量:编程中重要的两种数据类型
常量与变量 在编程中,我们常常需要存储一些数据。这些数据有些是恒定不变的,有些却是可以随时变化的。对于恒定不变的数据,我们称之为常量;对于可以变化的数据,我们则称之为变量。这两种数据类型在程序中非常重要&…...
( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数 难度:中等 给定一个包含 n 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。 假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。 你…...

【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...

武忠祥老师每日一题||定积分基础训练(三)
常用的基本不等式: sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...

Docker安装常用软件-Apollo(有问题)
零:apollo概念介绍 官网网站:GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址:mirrors / ctripcorp / apollo GitCode …...

f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点>x0必为|f(x)|的连续点) 注:”[a,b]连续“包括&#…...

今天面了一个来字节要求月薪23K,明显感觉他背了很多面试题...
最近有朋友去字节面试,面试前后进行了20天左右,包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说,80%的人都会栽在第一轮面试,要不是他面试前做足准备,估计都坚持不完后面几轮面试。 其实&…...
)
如何使用二元三次回归分析建立预测模型?(分析、原理、代码示例)
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型,常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型,其中包括两个自变量(通常…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
