如何评判算法好坏?复杂度深度解析
如何评判算法好坏?复杂度深度解析
- 1. 算法效率
- 1.1 如何衡量一个算法好坏
- 1.2 算法的复杂度
- 2 时间复杂度
- 2.1 时间复杂度的概念
- 2.1.1 实例
- 2.2 大O的渐进表示法
- 2.3 常见时间复杂度计算举例
- 3 空间复杂度
- 4 常见复杂度对比
- 5 结尾

1. 算法效率
1.1 如何衡量一个算法好坏
long long Fib(int N)
{if (N < 3){return 1;}return Fib(N - 1) + Fib(N - 2);
}
斐波那契数列的递归方式非常简洁,但简介一定好吗?那该如何衡量其好与坏呢?
1.2 算法的复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,及时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们已经不需要在特别关注一个算法的空间复杂度。
2 时间复杂度
2.1 时间复杂度的概念
时间复杂度的概念:在计算机科学中,算法的时间复杂度是一个函数,他定量描述了该算法的运行时间。
一个算法的运行时间,从理论上说是算不出来的,只有把你的程序放在机器上跑起来,才知道。但是我们需要每个算法都上机测试吗?
是都可以上机,但是这很麻烦,所以才有了时间复杂度这个分析方法。
一个算法所发费的时间和其中的语句执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即,找到某条语句与问题规模N之间的数学表达式,就是该算法的时间复杂度。
2.1.1 实例
我们先来看看这段代码:
void Func1(int N)
{int count = 0;for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){++count;}}for (int k = 0; k < 2 * N; k++){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);return 0;
}
Func1的执行次数:F(N)= N^2 + 2*n + 10
但在实际计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概的执行次数即可,那么这里我们就要用到大O的渐进表示法。
2.2 大O的渐进表示法
大O符号(Big O notation):用于描述函数渐进行为的函数符号。
推导大O阶方法:
①: 用常数1取代运行时间的所有加法常数。
②: 在修改后的运行次数函数中,只保留最高阶项。
③: 如果最高阶存在并且不是1,则去掉与这个项相乘的常数,得到的结果就是大O阶。
④: 有一些算法存在最好、最坏和平均的情况,但实际中一般关注的是算法的最坏运行情况。
所以使用大O的渐进表示法以后,Func1的时间复杂度为O(N^2).
通过上面我们很容易发现大O的渐进表示法去掉了那些对结果印象不大的项,简洁明了的表示执行次数。(本质上是计算属于那个量级)
2.3 常见时间复杂度计算举例
实例1:
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
3 空间复杂度
空间复杂度也是一个函数表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。
空间复杂度不是程序占用了多少byte的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度的计算规则基本和时间复杂度的计算类似,也用大O的渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间的复杂度主要是通过函数在运行时显示申请的额外空间来确定。
4 常见复杂度对比
一般算法的常见复杂度如下:

5 结尾
本篇博客到此就结束了。如果对你有帮助,记得三连哦。感谢您的支持!!!

相关文章:
如何评判算法好坏?复杂度深度解析
如何评判算法好坏?复杂度深度解析 1. 算法效率1.1 如何衡量一个算法好坏1.2 算法的复杂度 2 时间复杂度2.1 时间复杂度的概念2.1.1 实例 2.2 大O的渐进表示法2.3 常见时间复杂度计算举例 3 空间复杂度4 常见复杂度对比5 结尾 1. 算法效率 1.1 如何衡量一个算法好坏 …...

【HashMap】2352. 相等行列对
2352. 相等行列对 解题思路 使用哈希容器遍历grid数组 将每一行的字符全部转换为StringBuilde对象 然后存入map中遍历每一列 将其转换为字符串 然后查找Map中是否存在 如果存在 统计 class Solution {public int equalPairs(int[][] grid) {// 哈希容器Map<String,Intege…...

如何声明静态方法 和 实现?
如何声明静态方法 和 实现?在 C 中,声明和实现静态方法(静态成员函数)与普通成员函数有一些区别。静态方法属于类本身,而不是类的对象,因此在声明和实现时需要特殊的语法。 声明静态方法: 在类…...

哈工大计算机网络课程局域网详解之:无线局域网
哈工大计算机网络课程局域网详解之:无线局域网 文章目录 哈工大计算机网络课程局域网详解之:无线局域网IEEE 802.11无线局域网802.11体系结构802.11:信道与AP关联 本节介绍一下平时经常使用的一个无线局域网技术,也就是通常我们使…...
)
系统集成|第六章(笔记)
目录 第六章、整体管理6.1 项目整体管理概述6.2 主要过程6.2.1 制订项目章程6.2.2 制订项目管理计划6.2.3 指导与管理项目工作6.2.4 监控项目工作6.2.5 实施整体变更控制6.2.6 结束项目或阶段 上篇:第五章、立项管理 第六章、整体管理 6.1 项目整体管理概述 概述&a…...

MySQL主从复制环境部署
文章目录 MySQL主从复制什么是主从复制:为什么需要主从复制:配置文件修改-主:时间同步:重启服务-主:创建同步用户:查看主上的二进制文件名及位置:配置-从:测试:注: MySQL…...
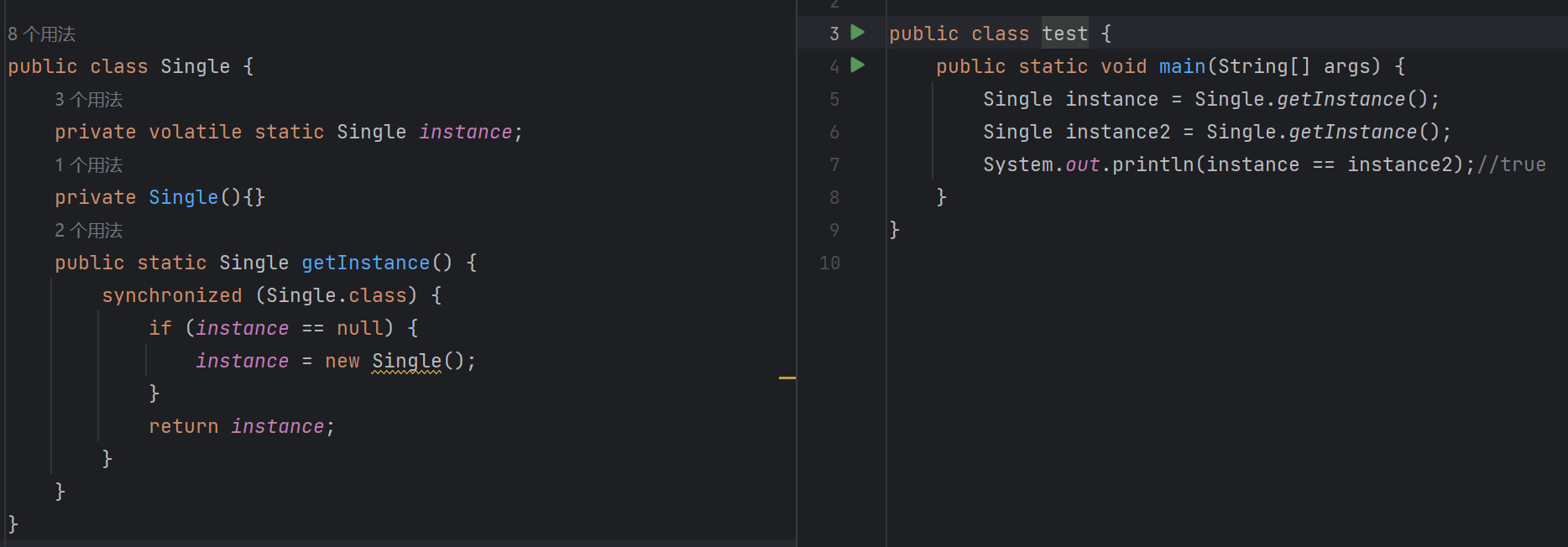
day42-servlet下拉查询/单例模式
0目录 1.Servlet实现下拉查询(两表) 2.单例模式 1.实战 1.1 创建工程,准备环境... 1.2 接口 1.3 重写方法 1.4 servlet 1.5 list.jsp list.jsp详解 2.单例模式 2.1 饿汉模式:在程序加载时直接创建对象&#…...

docker中设置容器健康检查
文章目录 一、docker-compose方式二、Dockerfile方式三、docker run方式四、查看检查日志 一、docker-compose方式 在docker-compose中加入healthcheck healthcheck 支持下列选项: test:健康检查命令,例如 ["CMD", "curl&quo…...

azure-cognitiveservices-speech api error while using with AWS Lambda
Azure 语音评估服务 Cancellation Reason 初始化平台失败 1.在mac上安装 pip install azure-cognitiveservices-speech1.30.0正常运行没有问题,服务部署到docker 容器中后调用Azure语音评估服务报错 Cancellation Reason 初始化平台失败 2.解决方案,变…...

系统集成项目管理工程师挣值分析笔记大全
系统集成项目管理工程师挣值分析笔记大全 挣值分析是一种项目管理技术,用于量化和监控项目绩效。它通过比较计划值(PV)、实际成本(AC)和挣值(EV)三个参数来评估项目的进展情况和成本绩效。 挣值…...
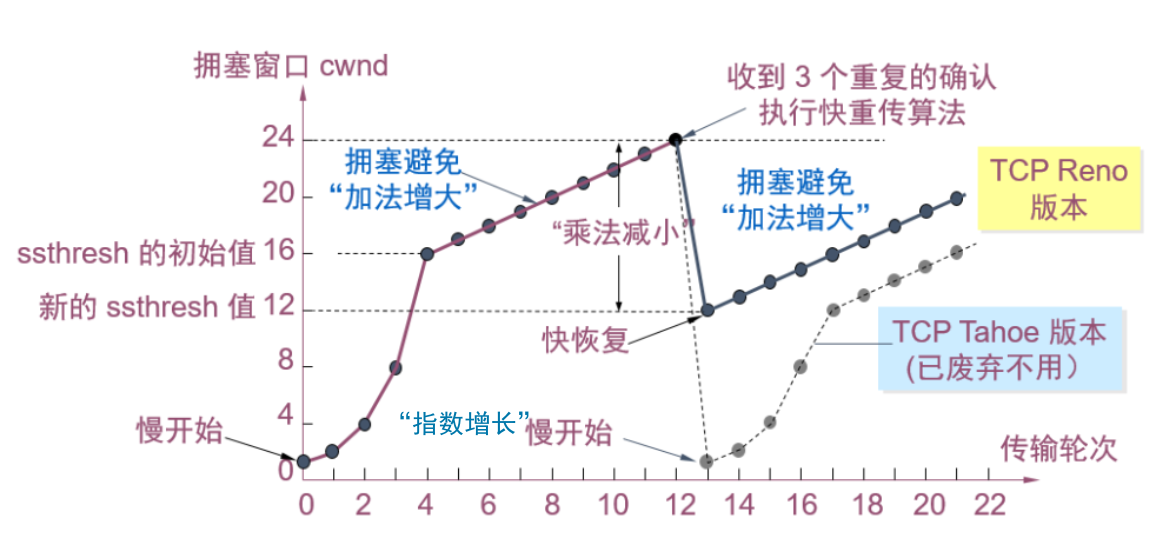
TCP 协议【传输层协议】
文章目录 1. 简介1.1 TCP 协议是什么1.2 TCP 协议的作用1.3 什么是“面向连接” 2. 简述 TCP2.1 封装和解包2.2 TCP 报文格式2.3 什么是“面向字节流”2.4 通过 ACK 机制实现一定可靠性 3. 详述 TCP3.1 基本认识TCP 报头格式16 位源/目标端口号32 位序列号*32 位确认应答号4 位…...
:time.Duration)
Golang 中的 time 包详解(二):time.Duration
在日常开发过程中,会频繁遇到对时间进行操作的场景,使用 Golang 中的 time 包可以很方便地实现对时间的相关操作。接下来的几篇文章会详细讲解 time 包,本文讲解一下 time 包中的 time.Duration 类型。 time.Duration time.Duration 类型是…...

Linux 学习记录58(ARM篇)
Linux 学习记录58(ARM篇) 本文目录 Linux 学习记录58(ARM篇)一、GIC相关寄存器1. 系统框图2. 中断号对应关系 二、GICD寄存器1. GICD_CTLR2. GICD_ISENABLERx3. GICD_IPRIORITYRx4. GICD_ITARGETSRx5. GICD_ICPENDRx 三、GICC寄存器1. GICC_PMR2. GICC_CTLR3. GICC_IAR4. GICC_…...
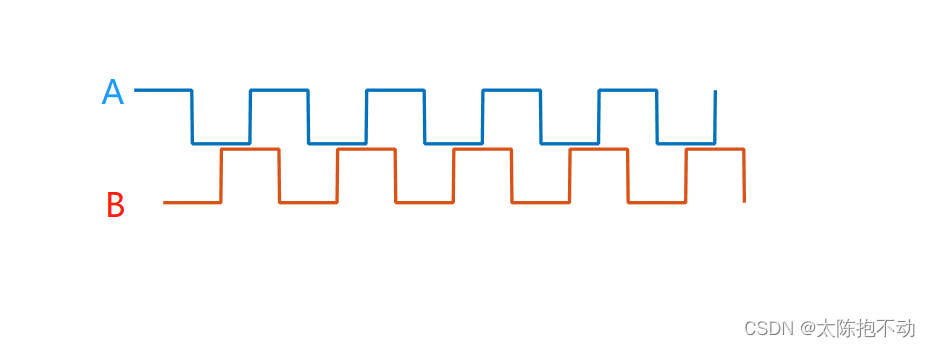
【一文搞懂】—带霍尔编码器的直流有刷减速电机
文章目录 一、直流有刷电机二、减速比三、霍尔编码器3.1 霍尔编码器3.2 霍尔编码器测速原理 四、测速程序设计4.1 跳变沿检测4.2 计算转速 一、直流有刷电机 宏观上说直流有刷电机由固定部分(定子)和旋转部分(转子)组成。在定子上…...

滴水逆向三期笔记与作业——02C语言——05 正向基础/05 循环语句
目录 一、缓冲区溢出的HelloWorld二、永不停止的HelloWorld三、基础知识3.1 变量的声明3.2 类型转换(一般用于小转大)3.3 表达式3.4 语句和程序块3.5 参数与返回值3.6 关系运算符3.7 逻辑运算符:&& || !3.8 单目运算符3.9 三目运算符…...

Python抓取分享页面的源代码示例
本文章是关于利用Python方法来抓取某网站分享页面中的源码方法示例。需要大家注意的是Python抓取分享页面的源代码示例,是要在运行时导入BeautifulSoup.py文件后才可以使用。 Python抓取分享页面的源代码示例,需要用到python urllib2模块方法࿰…...
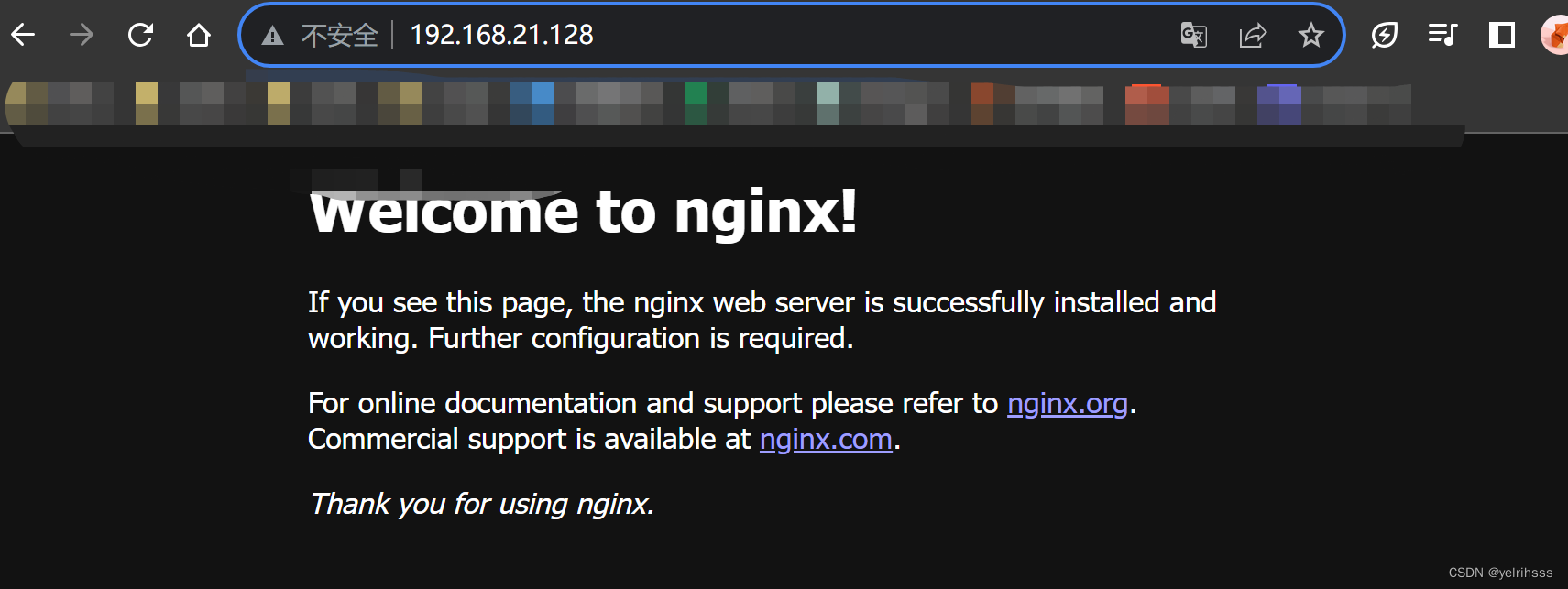
linux安装nginx遇到的报错
1、Linux如何修改只读文件(以设置自动连网为例) vim /etc/sysconfig/network-scripts/ifcfg-ens33 然后提示 E45:已设定选项“readonly”(请加!强制执行) 如果需要强制修改,可以使用࿰…...

一起学SF框架系列5.8-spring-Beans-Bean注解解析3-解析配置component-scan
本文主要讲述Spring是如何解析“context:component-scan”元素,扫描加载目录下的BeanDefinition。 解析内容 1、解析的元素如下: <!-- 注解模式:配置bean扫描路径(注:自动包含子路径) --><conte…...

【LeetCode热题100】打卡第42天:滑动窗口最大值搜索二维矩阵II
文章目录 【LeetCode热题100】打卡第42天:滑动窗口最大值&搜索二维矩阵II⛅前言 滑动窗口最大值🔒题目🔑题解 搜索二维矩阵II🔒题目🔑题解 【LeetCode热题100】打卡第42天:滑动窗口最大值&搜索二维…...

[uni-app] 微信小程序 - 组件找不到/导入报错 (分包问题导致)
文章目录 问题表现问题原因 问题表现 切换了个路径下的组件, 导入失败, 尝试了清缓存\重启\删项目等一些列操作均无效 上面两个路径中, 都存在一模一样的videItem.vue Main路径是可以导入的 Main路径是无法导入的 问题原因 后来发现, 是 分包的问题导致. 我们先来假设一个场…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
