Golang 中的 time 包详解(二):time.Duration
在日常开发过程中,会频繁遇到对时间进行操作的场景,使用 Golang 中的 time 包可以很方便地实现对时间的相关操作。接下来的几篇文章会详细讲解 time 包,本文讲解一下 time 包中的 time.Duration 类型。
time.Duration
time.Duration 类型是一个有符号的 int64 类型,以纳秒为单位,用来表示两个时间点之间的时长。类型定义如下:
type Duration int64拥有的方法如下:
- func (d Duration) Hours() float64,返回持续的时间,以小时为单位。
- func (d Duration) Minutes() float64,返回持续的时间,以分钟为单位。
- func (d Duration) Seconds() float64,返回持续的时间,以秒为单位。
- func (d Duration) Milliseconds() int64,返回持续的时间,以毫秒为单位。
- func (d Duration) Microseconds() int64,返回持续的时间,以微秒为单位。
- func (d Duration) Nanoseconds() int64,返回持续的时间,以纳秒为单位。
- func (d Duration) String() string,返回一个字符串类型的持续的时间,格式为 “72h3m0.5s”。示例如下:
package mainimport ("fmt""time"
)func main() {a := time.Duration(3) * time.Hourfmt.Println(a.Hours()) // 3fmt.Println(a.Minutes()) // 180fmt.Println(a.Seconds()) //10800fmt.Println(a.Milliseconds()) //10800000fmt.Println(a.Microseconds()) //10800000000fmt.Println(a.Nanoseconds()) //10800000000000fmt.Println(a.String()) //3h0m0s
}- func (d Duration) Round(m Duration) Duration,返回将 d 四舍五入到 m 的最接近倍数的结果。通过示例理解一下:
package mainimport ("fmt""time"
)func main() {a := time.Duration(10) * time.Minute// 结果为 10,10 正好是 1 的整数倍fmt.Println(a.Round(time.Duration(1) * time.Minute))// 结果为 9,3 的 3 倍是 9,3 的 4 倍是 12,9 和 10 离得更近fmt.Println(a.Round(time.Duration(3) * time.Minute))// 结果为 12,4 的 2 倍是 8,4 的 3 倍是 12,距离一样近往上入fmt.Println(a.Round(time.Duration(4) * time.Minute))// 结果为 10,10 正好是 5 的整数倍fmt.Println(a.Round(time.Duration(5) * time.Minute))// 结果为12, 6 的 1 倍是 6,6 的 2 倍是 12,10 离 12 更近fmt.Println(a.Round(time.Duration(6) * time.Minute))
}- func (d Duration) Truncate(m Duration) Duration,用于将 d 截断到 m 最近整数倍。通过示例理解一下:
package mainimport ("fmt""time"
)func main() {a := time.Duration(10) * time.Minute// 结果为 10,10 正好是 1 的整数倍fmt.Println(a.Truncate(time.Duration(1) * time.Minute))// 结果为 9,3 的 3 倍是 9,最接近 10fmt.Println(a.Truncate(time.Duration(3) * time.Minute))// 结果为 8,4 的 2 倍是 8,最接近 10fmt.Println(a.Truncate(time.Duration(4) * time.Minute))// 结果为 10,10 正好是 5 的整数倍fmt.Println(a.Truncate(time.Duration(5) * time.Minute))// 结果为 6,6 的 1 倍是 6,最接近 10fmt.Println(a.Truncate(time.Duration(6) * time.Minute))// 结果为 0,11 的 1 倍是11,大于了 10fmt.Println(a.Truncate(time.Duration(11) * time.Minute))
}加减法运算
因为 time.Duration 表示的是时间段,可以对 time.Duration 类型的值进行加减法运算,例如:
package mainimport ("fmt""time"
)func main() {a := time.Duration(10) * time.Minuteb := time.Duration(10) * time.Secondfmt.Println(a + b)fmt.Println(a - b)
}相关文章:
:time.Duration)
Golang 中的 time 包详解(二):time.Duration
在日常开发过程中,会频繁遇到对时间进行操作的场景,使用 Golang 中的 time 包可以很方便地实现对时间的相关操作。接下来的几篇文章会详细讲解 time 包,本文讲解一下 time 包中的 time.Duration 类型。 time.Duration time.Duration 类型是…...

Linux 学习记录58(ARM篇)
Linux 学习记录58(ARM篇) 本文目录 Linux 学习记录58(ARM篇)一、GIC相关寄存器1. 系统框图2. 中断号对应关系 二、GICD寄存器1. GICD_CTLR2. GICD_ISENABLERx3. GICD_IPRIORITYRx4. GICD_ITARGETSRx5. GICD_ICPENDRx 三、GICC寄存器1. GICC_PMR2. GICC_CTLR3. GICC_IAR4. GICC_…...
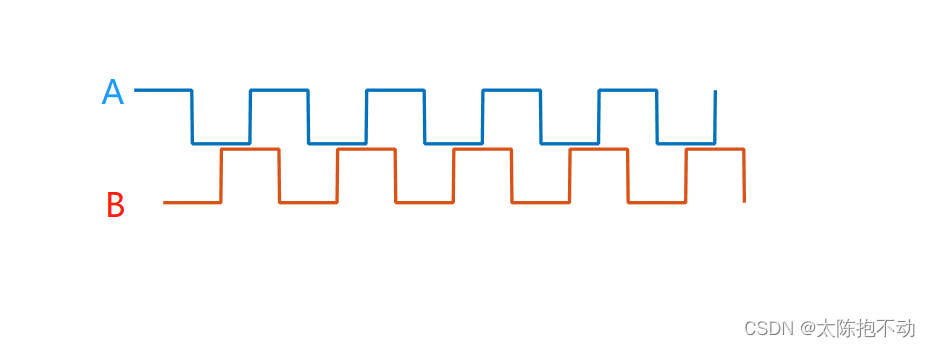
【一文搞懂】—带霍尔编码器的直流有刷减速电机
文章目录 一、直流有刷电机二、减速比三、霍尔编码器3.1 霍尔编码器3.2 霍尔编码器测速原理 四、测速程序设计4.1 跳变沿检测4.2 计算转速 一、直流有刷电机 宏观上说直流有刷电机由固定部分(定子)和旋转部分(转子)组成。在定子上…...

滴水逆向三期笔记与作业——02C语言——05 正向基础/05 循环语句
目录 一、缓冲区溢出的HelloWorld二、永不停止的HelloWorld三、基础知识3.1 变量的声明3.2 类型转换(一般用于小转大)3.3 表达式3.4 语句和程序块3.5 参数与返回值3.6 关系运算符3.7 逻辑运算符:&& || !3.8 单目运算符3.9 三目运算符…...

Python抓取分享页面的源代码示例
本文章是关于利用Python方法来抓取某网站分享页面中的源码方法示例。需要大家注意的是Python抓取分享页面的源代码示例,是要在运行时导入BeautifulSoup.py文件后才可以使用。 Python抓取分享页面的源代码示例,需要用到python urllib2模块方法࿰…...
linux安装nginx遇到的报错
1、Linux如何修改只读文件(以设置自动连网为例) vim /etc/sysconfig/network-scripts/ifcfg-ens33 然后提示 E45:已设定选项“readonly”(请加!强制执行) 如果需要强制修改,可以使用࿰…...

一起学SF框架系列5.8-spring-Beans-Bean注解解析3-解析配置component-scan
本文主要讲述Spring是如何解析“context:component-scan”元素,扫描加载目录下的BeanDefinition。 解析内容 1、解析的元素如下: <!-- 注解模式:配置bean扫描路径(注:自动包含子路径) --><conte…...

【LeetCode热题100】打卡第42天:滑动窗口最大值搜索二维矩阵II
文章目录 【LeetCode热题100】打卡第42天:滑动窗口最大值&搜索二维矩阵II⛅前言 滑动窗口最大值🔒题目🔑题解 搜索二维矩阵II🔒题目🔑题解 【LeetCode热题100】打卡第42天:滑动窗口最大值&搜索二维…...

[uni-app] 微信小程序 - 组件找不到/导入报错 (分包问题导致)
文章目录 问题表现问题原因 问题表现 切换了个路径下的组件, 导入失败, 尝试了清缓存\重启\删项目等一些列操作均无效 上面两个路径中, 都存在一模一样的videItem.vue Main路径是可以导入的 Main路径是无法导入的 问题原因 后来发现, 是 分包的问题导致. 我们先来假设一个场…...

从零构建医疗领域知识图谱的KBQA问答系统:其中7类实体,约3.7万实体,21万实体关系。
项目设计集合(人工智能方向):助力新人快速实战掌握技能、自主完成项目设计升级,提升自身的硬实力(不仅限NLP、知识图谱、计算机视觉等领域):汇总有意义的项目设计集合,助力新人快速实…...
编程小白的自学笔记十二(python爬虫入门四Selenium的使用实例二)
系列文章目录 编程小白的自学笔记十一(python爬虫入门三Selenium的使用实例详解) 编程小白的自学笔记十(python爬虫入门二实例代码详解) 编程小白的自学笔记九(python爬虫入门代码详解) 目录 系列文章…...

技术笔记2023076 rBoot学习7
技术笔记2023076 rBoot学习7 继续之前的学习。 代码分析:函数find_image() // prevent this function being placed inline with main // to keep mains stack size as small as possible // dont mark as static or itll be optimised out when // using the ass…...
收藏这6个抠图工具,一键抠图不用愁!
在图片编辑工作中,抠图是设计师常用的操作。随着设计工具的不断增加,抠图操作摆脱了过去繁琐的操作步骤,几乎可以一键完成。今天本文将为大家介绍6个好用的抠图工具,一起来看看吧! 1、皮卡智能抠图 皮卡智能抠图是一…...
四,Eureka 第四章
2.1.3 增加依赖 <!--添加依赖--><dependencies><!--Eureka Server--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId></dependency>&l…...
k8s常见的资源对象使用
目录 一、kubernetes内置资源对象 1.1、kubernetes内置资源对象介绍 1.2、kubernetes资源对象操作命令 二、job与cronjob计划任务 2.1、job计划任务 2.2、cronjob计划任务 三、RC/RS副本控制器 3.1、RC副本控制器 3.2、RS副本控制器 3.3、RS更新pod 四、Deployment副…...
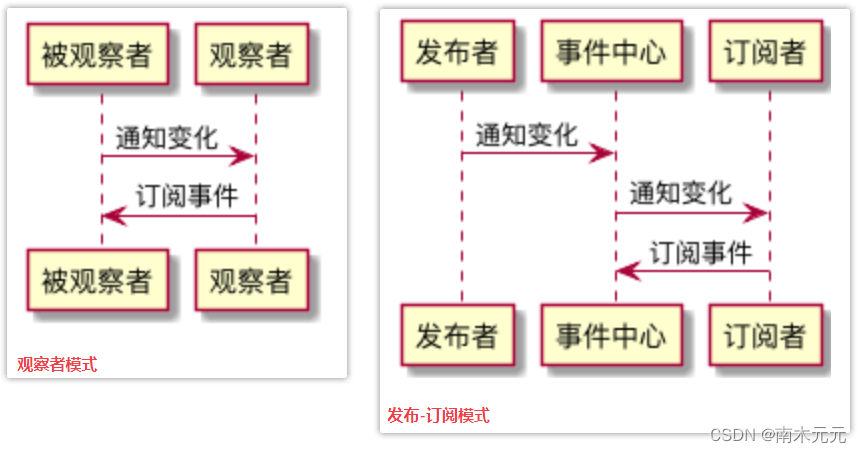
JavaScript 简单实现观察者模式和发布订阅模式
JavaScript 简单实现观察者模式和发布订阅模式 1. 观察者模式1.1 如何理解1.2 代码实现 2. 发布订阅模式2.1 如何理解2.2 代码实现 1. 观察者模式 1.1 如何理解 概念:观察者模式定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变时ÿ…...
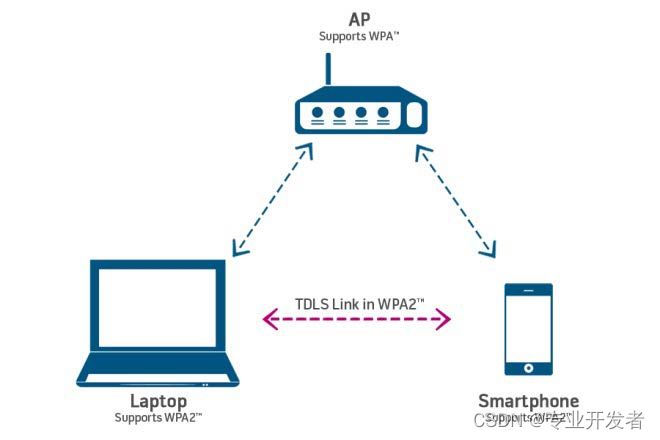
高通WLAN框架学习(37)-- TDLS(Tunneled Direct Link Setup)通道直接链路建立
一 TDLS概述 隧道直连设置(TDLS)基于IEEE 802.11z-2010IEEE标准802.11z标准(无线局域网介质访问控制(MAC)和物理层(PHY)规范。 TDLS允许与同一AP关联的设备之间建立直接链路。Wi-Fi Direct允许设备之间直接连接,而不需要AP。Wi-Fi联盟认证可用于IEEE 802.11a和802.11g设备的T…...

高算力AI模组前沿应用:基于ARM架构的SoC阵列式服务器
本期我们带来高算力AI模组前沿应用,基于ARM架构的SoC阵列式服务器相关内容。澎湃算力、创新架构、异构计算,有望成为未来信息化社会的智能算力底座。 ▌性能优势AI驱动,ARM架构服务器加速渗透 一直以来,基于ARM架构的各类处理器…...

老年公寓人员定位管理系统:提升安全与关怀的智能解决方案
老年公寓作为提供安全居住环境和关怀服务的重要场所,面临着人员管理和安全控制的挑战。为了解决这些问题,老年公寓人员定位管理系统应运而生。基于为提供全面的安全管理和个性化关怀服务,华安联大便通过老年公寓人员定位管理系统的技术原理、…...

每日一题之两个字符串的删除操作
题目链接 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 **相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 示例 1: 输入: word1 "sea", word2 "eat" 输出: 2 解释: 第一步将 "sea" 变…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用
Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用 Linux 内核内存管理是构成整个内核性能和系统稳定性的基础,但这一子系统结构复杂,常常有设置失败、性能展示不良、OOM 杀进程等问题。要分析这些问题,需要一套工具化、…...

【笔记】结合 Conda任意创建和配置不同 Python 版本的双轨隔离的 Poetry 虚拟环境
如何结合 Conda 任意创建和配置不同 Python 版本的双轨隔离的Poetry 虚拟环境? 在 Python 开发中,为不同项目配置独立且适配的虚拟环境至关重要。结合 Conda 和 Poetry 工具,能高效创建不同 Python 版本的 Poetry 虚拟环境,接下来…...
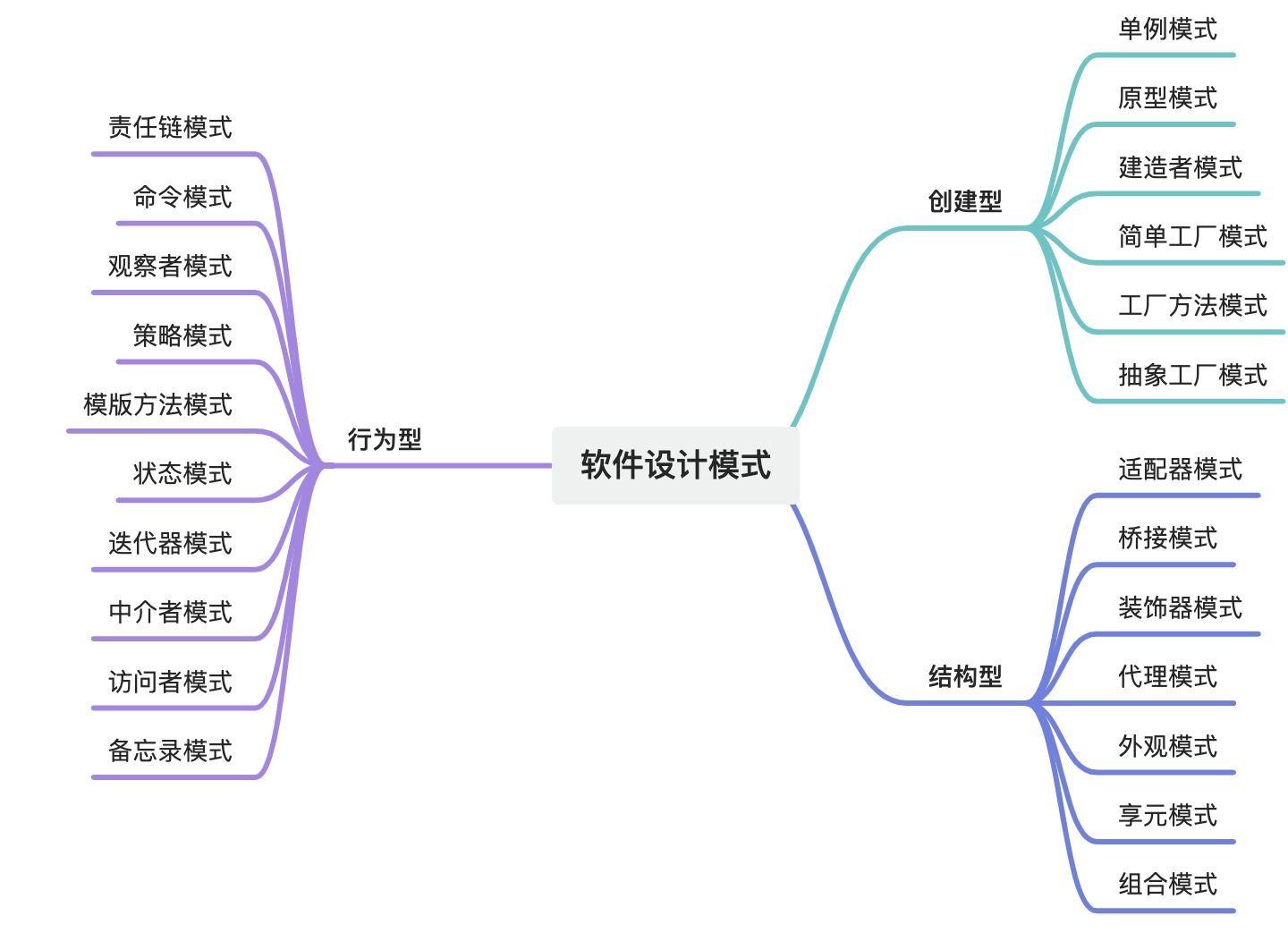
设计模式域——软件设计模式全集
摘要 软件设计模式是软件工程领域中经过验证的、可复用的解决方案,旨在解决常见的软件设计问题。它们是软件开发经验的总结,能够帮助开发人员在设计阶段快速找到合适的解决方案,提高代码的可维护性、可扩展性和可复用性。设计模式主要分为三…...
