Vue项目中强制刷新页面的方法
我们在动态切换组件的过程中，导航栏和底栏不动，动态切换中间区域的情况，在首页可以进行跳转任意组件，在组件与组件之间不能相互跳转，路由发生了变化，但是页面未改变，这时我们就需要强制刷新页面。
强制刷新页面的方式有三种：
①location.reload()
②this.$router.go(0)
前面两种方法都有些简单粗暴，主要说一下第三种方法
③provide 配合 inject
首先我们需要在App.vue中修改
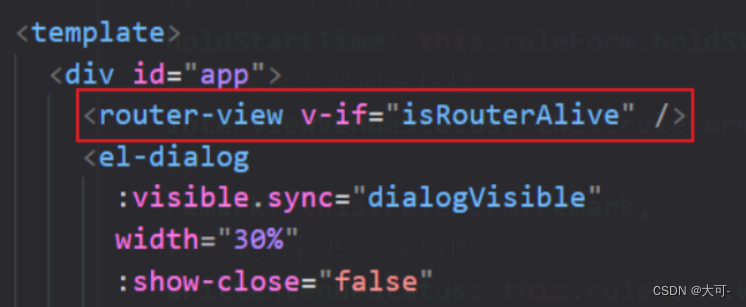
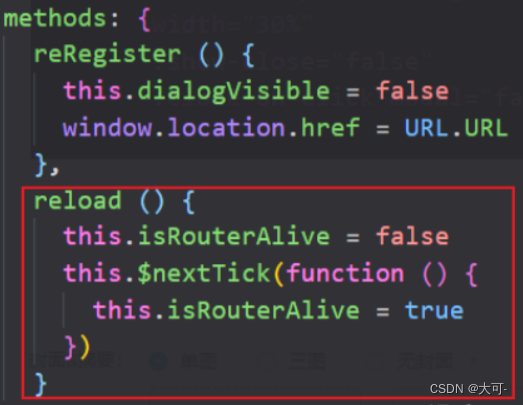
通过定义reload方法，控制router-view的显隐（生成和销毁）
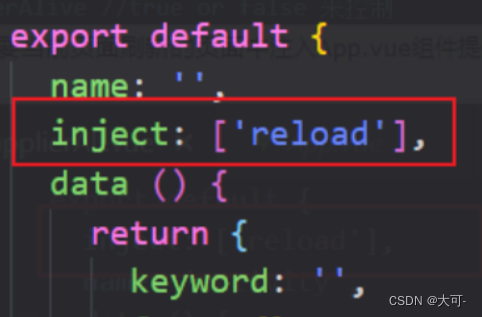
然后在需要刷新页面的组件中注入依赖，注入时inject后面是上面的方法名称
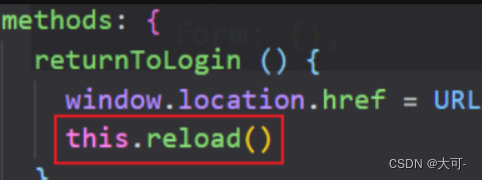
最后直接调用reload方法就能实现页面的刷新
相关文章：
Vue项目中强制刷新页面的方法
我们在动态切换组件的过程中，导航栏和底栏不动，动态切换中间区域的情况，在首页可以进行跳转任意组件，在组件与组件之间不能相互跳转，路由发生了变化，但是页面未改变，这时我们就需要强制刷新页面…...
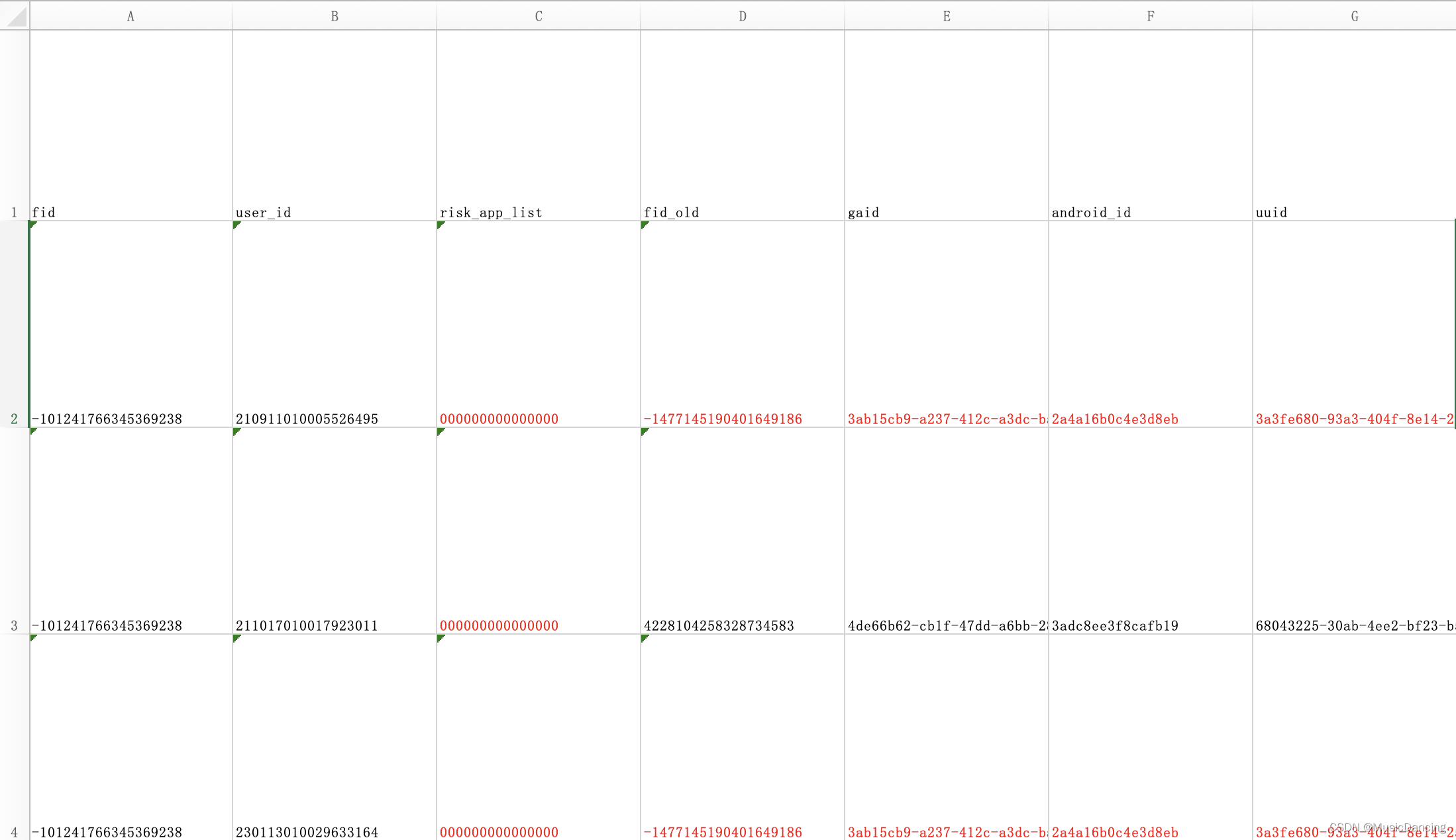
文件按关键字分组-切割-染色-写入excel
1. 背景 针对下面的文件data.csv，首先根据fid进行排序，然后分组，使相同fid的记录放到同一个excel文件中，并对每列重复的数据元素染上红色。 fid,user_id -1000078398032092029,230410010036537520 -1000078398032092029,23042301…...
爬虫的基本原理：爬虫概述及爬取过程
前言 随着互联网的不断发展和普及，我们的生活越来越离不开网络。而网络世界中有着海量的信息和数据，这些信息和数据对于我们的工作和生活都有很大的帮助。但是，如何高效地获取这些数据呢？这时候，爬虫这个工具就派上用…...
cocos2D插件转3D插件
cocos2D插件转3D插件 use strict;/*** 3d插件api映射,兼容2d插件* */let fs require("fs");let path require("path");let baseDir ;const prsPath (Editor.Project && Editor.Project.path ? Editor.Project.path : Editor.remote.projectP…...
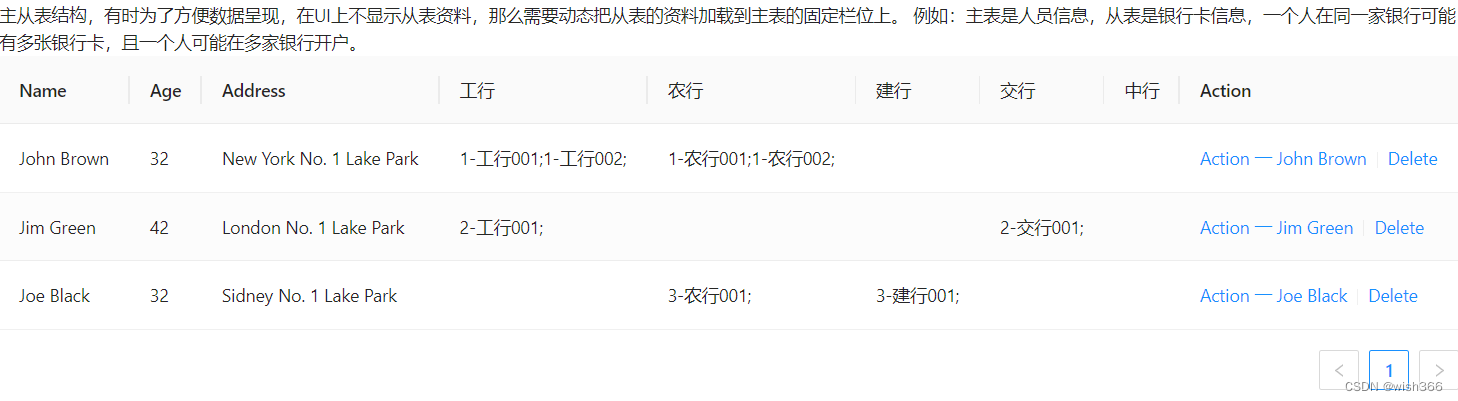
[Angular] 主从表结构，从表记录在主表固定栏位上呈现
Background 主从表结构，有时为了方便数据呈现，在UI上不显示从表资料，那么需要动态把从表的资料加载到主表的固定栏位上。 例如：主表是人员信息，从表是银行卡信息，一个人在同一家银行可能有多张银行卡&…...
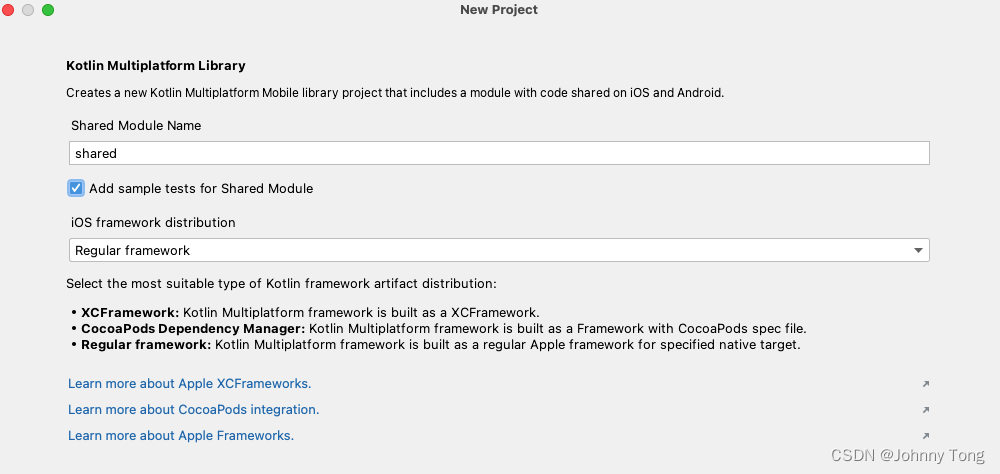
Kotlin Multiplatform 创建多平台分发库
目标：通过本教程学习如何使用 Kotlin Multiplatform Library 创建多平台分发库(iOS，安卓)。 创建一个项目 1、本教程使用的是Android Studio创建 2、选择 新建工程，选择 Kotlin Multiplatform Library 3、点击next 输入需要创建的项目名称以…...
[SQL挖掘机] - union/union all 使用注意事项
因为当使用union和union all操作符时，有一些注意事项需要考虑： 1. 列数和数据类型匹配： 要使用union或union all合并结果集，两个或多个查询的 select 语句必须返回相同数量和类型的列。确保每个查询返回相同的列数，并…...
php 单例模式
1，单例模式，属于创建设计模式，简单来说就是一个类只能有一个实例化对象，并提供一个当前类的全局唯一可访问入口； 2，例子 <?phpclass Singleton {private static $instance null;// 禁止被实例化priva…...
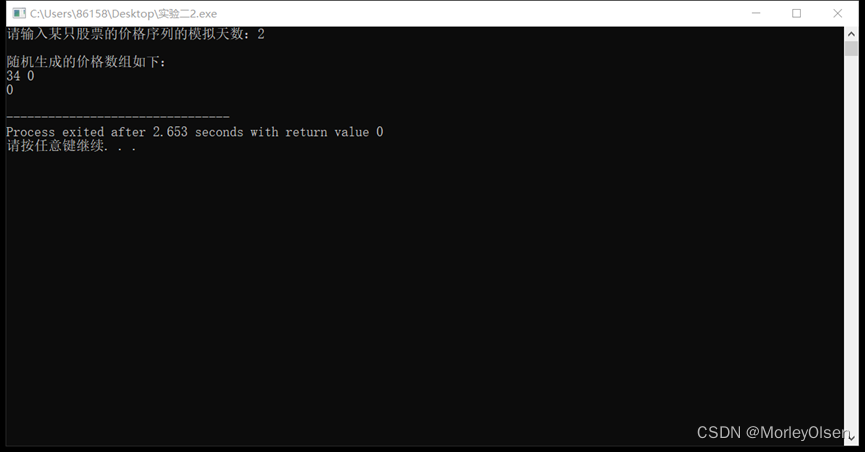
【数据结构】实验二：顺序表
实验二 顺序表 一、实验目的与要求 1）熟悉顺序表的类型定义； 2）熟悉顺序表的基本操作； 3）灵活应用顺序表解决具体应用问题。 二、实验内容 1）在一个整数序列a1,a2,…,an中，若存在一个数&…...
【高级数据结构】线段树
目录 最大数（单点修改，区间查询） 线段树1（区间修改，区间查询） 最大数（单点修改，区间查询） 洛谷：最大数https://www.luogu.com.cn/problem/P1198 题目描述 …...
qt简易闹钟
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);ui->stopBtn->setDisabled(true);this->setFixedSize(this->size()); //设置固定大小this->s…...
python和c加加有什么区别,c和c++和python先学哪个
本篇文章给大家谈谈c加加编程和python编程有什么区别，以及python和c加加有什么区别，希望对各位有所帮助，不要忘了收藏本站喔。 1、python和c学哪个好 学C好。 C通常比Python更快，因为C是一种编译型语言，而Python则是…...
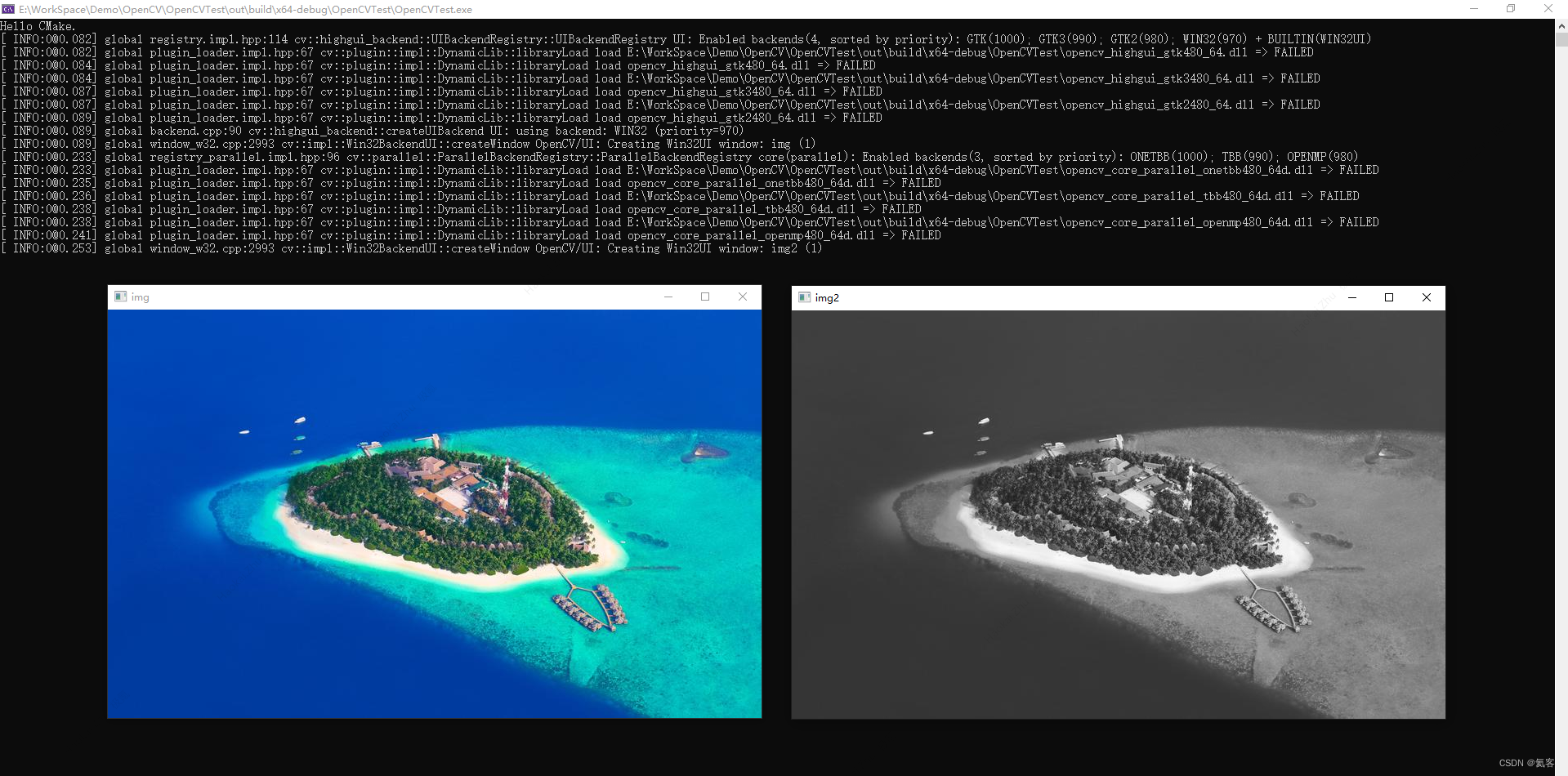
Visual Studio 2022 cmake配置opencv开发环境
1. 环境与说明 这里我用的是 widnows 10 64位，Visual Studio 用的 Visual Studio Community 2022 (社区版) 对于Android开发工程师来说，为什么要使用Visual Studio 呢 ? 因为在Visual Studio中开发调试OpenCV方便，可以开发调试好后…...
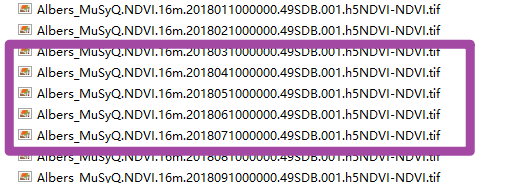
C++ GDAL找出多时相遥感影像缺失的日期并自动生成新的全零图像作为替补
本文介绍基于C 语言的GDAL库，基于一个存储大量遥感影像的文件夹，依据每一景遥感影像的文件名中表示日期的那个字段，找出这些遥感影像中缺失的成像日期，并新生成多个像元值全部为0的栅格文件，作为这些缺失日期当日的遥感…...
【AI底层逻辑】——篇章5（下）：机器学习算法之聚类降维时间序列
续上： 目录 4、聚类 5、降维 6、时间序列 三、无完美算法 往期精彩： 4、聚类 聚类即把相似的东西归在一起，与分类不同的是，聚类要处理的是没有标签的数据集，它根据样本数据的分布特性自动进行归类。 人在认知是…...
P1980 [NOIP2013 普及组] 计数问题
[NOIP2013 普及组] 计数问题 题目描述 试计算在区间 1 1 1 到 n n n 的所有整数中，数字 x x x（ 0 ≤ x ≤ 9 0\le x\le9 0≤x≤9）共出现了多少次？例如，在 1 1 1 到 11 11 11 中，即在 1 , 2 , 3 , 4…...
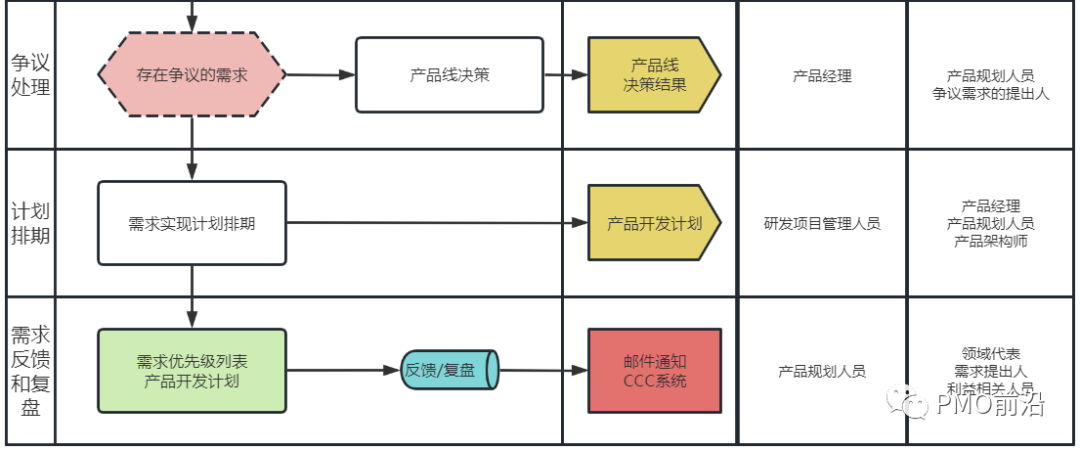
需求管理全过程流程图及各阶段核心关注点详解
分析报告指出，多达76%的项目失败是因为差劲的需求管理，这个是项目失败的最主要原因，比落后的技术、进度失控或者混乱的变更管理还要关键。很多项目往往在开始的时候已经决定了失败，谜底就在谜面上，开始就注定的失败&am…...
Android开源 自定义emoji键盘，EmojiPack v2.1版本
目录 一，简介 二、安装 添加jitpack 仓库 添加依赖: 混淆规则: 三、使用 1、一次性配置emoji显示处理 二、emoji的自定义键盘的使用 一，简介 EmojiPack当前已提供emoji的显示和emoji的选择自定义键盘，在emoji显示这一方面࿰…...
SOLIDWORKS软件的优势分析 硕迪科技
在现代的机械设计领域，SOLIDWORKS是一款备受青睐三维设计软件，它具备强大的建模和设计功能，在全球范围内广泛应用于机械设计和工程领域，为用户提供了全面的工程解决方案。本文就SOLIDWORKS的优势进行详细分析。 1、易于学习和使用…...
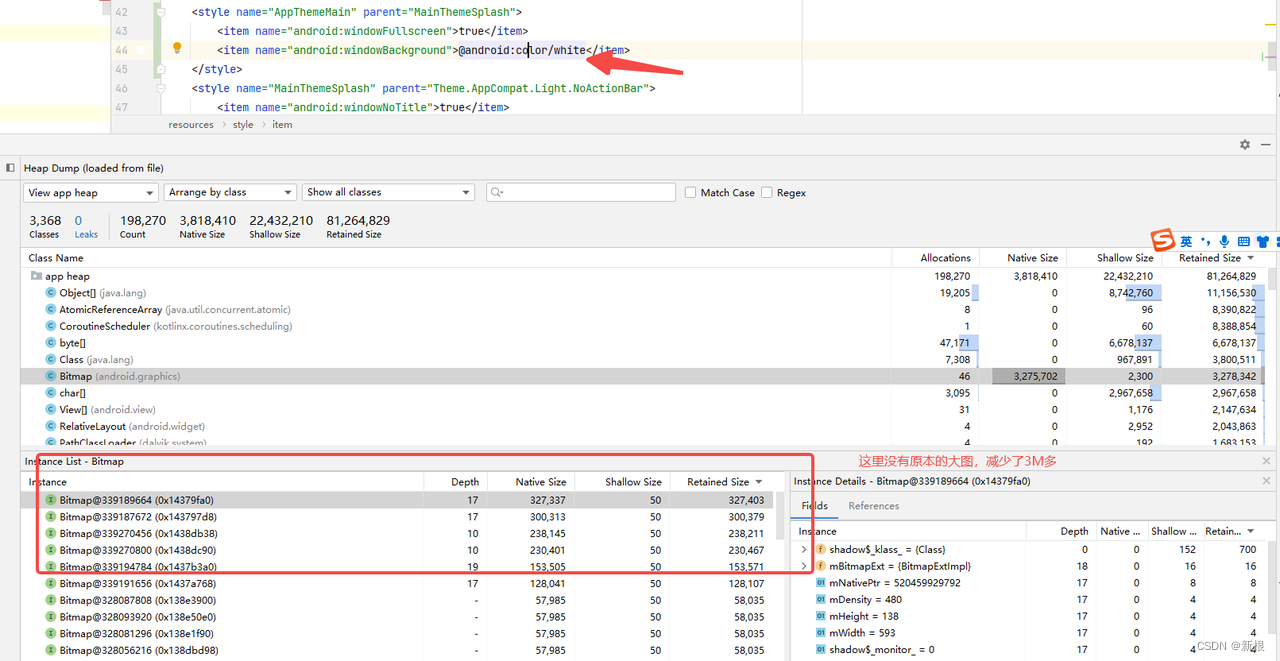
Android性能优化之游戏的Theme背景图
近期，对游戏的内存优化，通过内存快照发现，某个Activity的theme背景图 占用3M 多。考虑着手对齐进行优化。 问题 查看游戏中的内存快照，发现有一个图片bitmap 占用3M 多，设置在Activity的背景中： 查看Phon…...
遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...
基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先，你可以运行以下命令查看可用版本： apt-cache madison nginx-core输出示例： nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...
大语言模型如何处理长文本？常用文本分割技术详解
为什么需要文本分割？ 引言：为什么需要文本分割？一、基础文本分割方法1. 按段落分割（Paragraph Splitting）2. 按句子分割（Sentence Splitting）二、高级文本分割策略3. 重叠分割（Sliding Window）4. 递归分割（Recursive Splitting）三、生产级工具推荐5. 使用LangChain的…...
页面渲染流程与性能优化
页面渲染流程与性能优化详解（完整版） 一、现代浏览器渲染流程（详细说明） 1. 构建DOM树 浏览器接收到HTML文档后，会逐步解析并构建DOM（Document Object Model）树。具体过程如下： (…...
【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验
系列回顾： 在上一篇中，我们成功地为应用集成了数据库，并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了！但是，如果你仔细审视那些 API，会发现它们还很“粗糙”：有…...
OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式：dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一，腐蚀跟膨胀属于反向操作，膨胀是把图像图像变大，而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？
现有的 Redis 分布式锁库（如 Redisson）相比于开发者自己基于 Redis 命令（如 SETNX, EXPIRE, DEL）手动实现分布式锁，提供了巨大的便利性和健壮性。主要体现在以下几个方面： 原子性保证 (Atomicity)ÿ…...
手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读，综合法规核心要求、最新修正及企业合规要点： 一、法规背景与目标 生效与强制时间 发布于2023年8月31日（OJ公报&…...
wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像（比如分辨率3000*3000的图像）的办法，尤其是想把内存中的裸数据（只有图像的数据，不包…...