《算法竞赛·快冲300题》每日一题:“最小生成树”
《算法竞赛·快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。
文章目录
- 题目描述
- 题解
- C++代码
- Java代码
- Python代码
“ 最小生成树” ,链接: http://oj.ecustacm.cn/problem.php?id=1804
题目描述
【题目描述】
在平面中有n个点(xi,yi),两点之间的距离为欧几里得距离的平方。
求最小生成树的权重。
平面坐标满足:(0≤xi≤1000000,0≤yi≤10)
【输入格式】 输入第一行为正整数n,n不超过100000。
接下来n行,每行两个整数x和y,表示坐标点(x,y)。
【输出格式】 输出一个数表示答案。
【输入样例】
10
83 10
77 2
93 4
86 6
49 1
62 7
90 3
63 4
40 10
72 0
【输出样例】
660
题解
本题差不多是一道最小生成树的模板题,但是需要处理好边。本题的任意两点间有边,边的总数量约为 n 2 / 2 n^2/2 n2/2,而n最大是 1 0 6 10^6 106, n 2 / 2 n^2/2 n2/2条边显然会超出空间限制。
能否减少边的数量?注意到本题所有点的y坐标的限制是0≤yi≤10,这n个点的y坐标都在0和10之间。在平面上画11根横线;y=0,y=1,…,y=11,那么n个点都会在这11根线上。当处理到第i点时,只要把它和左边的11根线上的最近点连接,并且把它与右边的11根线上的最近点连接即可。这样得到的边,仍然会连通所有点,并且保留了最短的边。这样,每个点只需要连22个边,总边数只有22×n条。
不过还可以简化,对每个点,只连它左边的11条边即可,不用连右边的边,请思考为什么。
处理好边后,其他代码就是标准的最小生成树的模板。本题的边数不多,用代码比较简单的Kruskal算法编码。
【笔记】 最小生成树。
C++代码
#include<bits/stdc++.h>
using namespace std;
#define Mul(a) ((long long)(a) * (a))
const int N = 1e5 + 10;
typedef pair<int, int> Node;
int n, m; //点、边
Node a[N]; //n个点的坐标
struct edge{int u, v;long long w;
}e[N * 22]; //边的数量。如果只连左边的11条边,这里改为N*11
bool cmp(edge a, edge b){ return a.w < b.w;} //从小到大排序
void add_edge(int u, int v) { //点u和点v连边m++;e[m].u = u;e[m].v = v;e[m].w = Mul(a[u].first - a[v].first) + Mul(a[u].second - a[v].second);
}
int s[N];//并查集
int find_set(int x){ //查询并查集,返回x的根if(x != s[x])s[x] = find_set(s[x]); //路径压缩return s[x];
}
void kruskal(){for(int i = 1; i <= n; i++) s[i] = i; //并查集初始化sort(e + 1, e + 1 + m,cmp); //边排序long long ans = 0;for(int i = 1; i <= m; i++){ //从小到大遍历边,加入到最小生成树int u = find_set(e[i].u), v = find_set(e[i].v);if(u==v) continue; //产生了圈,丢弃else s[u] = v, ans += e[i].w;}cout<<ans<<endl;
}
int Last[15];
int main(){cin >> n;for(int i = 1; i <= n; i++) cin >> a[i].first >> a[i].second;sort(a + 1, a + 1 + n); //对点排序。实际是对x从小到大排序//每个点往每行的左边最近点连边for(int i = 0; i <= 10; i++) Last[i] = 0;for(int i = 1; i <= n; i++) {for(int y = 0; y <= 10; y++)if(Last[y]) add_edge(i, Last[y]);Last[a[i].second] = i;}//每个点往每行的右边最近点连边。可以省略/* for(int i = 0; i <= 10; i++)Last[i] = 0;for(int i = n; i >= 1; i--) {for(int y = 0; y <= 10; y++)if(Last[y]) add_edge(i, Last[y]);Last[a[i].second] = i;}*/kruskal();return 0;
}Java代码
import java.util.*;public class Main {static class Node implements Comparable<Node>{int x, y;Node(int x, int y) {this.x = x;this.y = y;}public int compareTo(Node o) {return Integer.compare(this.x, o.x);}}static class Edge implements Comparable<Edge>{int u, v;long w;Edge(int u, int v, long w) {this.u = u;this.v = v;this.w = w;}public int compareTo(Edge o) {return Long.compare(this.w, o.w);}}static final int N = 1_00_005;static Node[] a = new Node[N];static Edge[] e = new Edge[N * 11];static int[] s = new int[N];static int[] Last = new int[15];static int n, m;static long mul(int a) { return (long)a * a; }static void addEdge(int u, int v) {m++;e[m] = new Edge(u, v, mul(a[u].x - a[v].x) + mul(a[u].y - a[v].y));}static int findSet(int x) {if (x != s[x])s[x] = findSet(s[x]);return s[x];}static void kruskal() {for (int i = 1; i <= n; i++) s[i] = i;Arrays.sort(e, 1, m + 1);long ans = 0;for (int i = 1; i <= m; i++) {int u = findSet(e[i].u), v = findSet(e[i].v);if (u == v) continue;s[u] = v;ans += e[i].w;}System.out.println(ans);}public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();for (int i = 1; i <= n; i++) {int x = sc.nextInt(), y = sc.nextInt();a[i] = new Node(x, y);}Arrays.sort(a, 1, n + 1);for (int i = 0; i <= 10; i++) Last[i] = 0;for (int i = 1; i <= n; i++) {for (int y = 0; y <= 10; y++) if (Last[y] > 0) addEdge(i, Last[y]);Last[a[i].y] = i;}kruskal();}
}Python代码
from typing import List, Tuple
def mul(b): return b * b
class Node:def __init__(self, x: int, y: int):self.x = xself.y = ydef __lt__(self, other: "Node") -> bool:return self.x < other.x
class Edge:def __init__(self, u: int, v: int, w: int):self.u = uself.v = vself.w = wdef __lt__(self, other: "Edge") -> bool:return self.w < other.w
N = 100005
a: List[Node] = [Node(0, 0) for i in range(N)]
e: List[Edge] = [Edge(0, 0, 0) for i in range(N * 11)]
s: List[int] = [i for i in range(N)]
Last: List[int] = [0] * 15
n = m = 0
def addEdge(u: int, v: int) -> None:global mm += 1e[m].u = ue[m].v = ve[m].w = mul(a[u].x - a[v].x) + mul(a[u].y - a[v].y)def findSet(x: int) -> int:global sif x != s[x]: s[x] = findSet(s[x])return s[x]def kruskal() -> None:global n, m, s, efor i in range(1, n + 1): s[i] = ie[1:] = sorted(e[1:m + 1])ans = 0for i in range(1, m + 1):u = findSet(e[i].u)v = findSet(e[i].v)if u == v: continues[u] = vans += e[i].wprint(ans)
if __name__ == "__main__":n = int(input())for i in range(1, n + 1):x, y = map(int, input().split())a[i] = Node(x, y)a[1:] = sorted(a[1:n + 1])Last = [0] * 15for i in range(1, n + 1):for y in range(11):if Last[y] > 0: addEdge(i, Last[y])Last[a[i].y] = ikruskal()相关文章:

《算法竞赛·快冲300题》每日一题:“最小生成树”
《算法竞赛快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。 所有题目放在自建的OJ New Online Judge。 用C/C、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。 文章目录 题目描述题解C代码Java代码Python代码 “ 最…...

mysql的主键选择
一.没有定义主键有什么问题 如果定义了主键,那么InnoDB会使用主键作为聚簇索引如果没有定义主键,那么会使用第一非空的唯一索引(NOT NULL and UNIQUE INDEX)作为聚簇索引如果既没有主键也找不到合适的非空索引,那么In…...

Eureka 学习笔记1:服务端实例缓存
版本 awsVersion ‘1.11.277’ 缓存类型registryConcurrentHashMap<String, Map<String, Lease<InstanceInfo>>>AbstractInstanceRegistry成员变量readWriteCacheMapLoadingCacheResponseCacheImpl成员变量readOnlyCacheMapConcurrentMap<Key, Value>…...

vue : 无法加载文件 C:\Users\86182\AppData\Roaming\npm\vue.ps1,因为在此系统上禁止运行脚本。
windows11: PS E:\VueProjects> vue vue : 无法加载文件 C:\Users\86182\AppData\Roaming\npm\vue.ps1,因为在此系统上禁止运行脚本。有关详细信息,请参阅 https:/ go.microsoft.com/fwlink/?LinkID135170 中的 about_Execution_Policie…...
FLinkCDC读取MySQl时间戳时区相关问题解决汇总
FlinkCDC时间问题timestamp等https://blog.csdn.net/qq_30529079/article/details/127809317 FLinkCDC读取MySQl中的日期问题https://blog.csdn.net/YPeiQi/article/details/130265653 关于flink1.11 flink sql使用cdc时区差8小时问题https://blog.csdn.net/weixin_44762298/…...

第三篇-Tesla P40+CentOS7+CUDA 11.7 部署实践
硬件环境 系统:CentOS-7 CPU: 14C28T 显卡:Tesla P40 24G 准备安装 驱动: 515 CUDA: 11.7 cuDNN: 8.9.2.26 安装依赖 yum clean all yum update yum install -y gcc gcc-c pciutils kernel-devel-$(uname -r) kernel-headers-$(uname -r)查看GPU信息…...
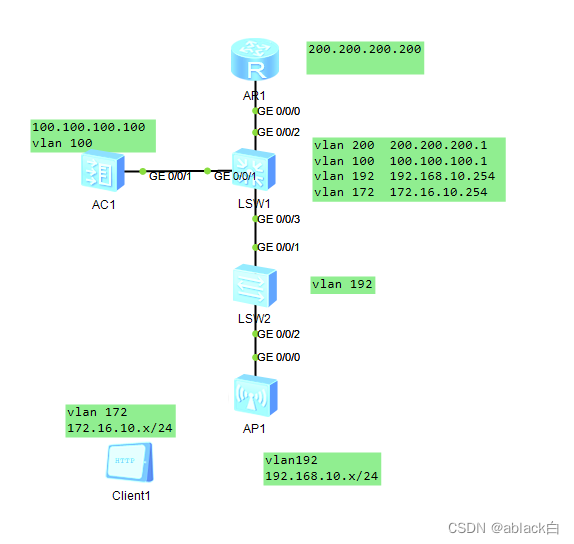
AC+FIT(瘦AP)配置浅谈
FIT ensp实验材料 :pc、路由器、三层交换机、二层交换机、ac、ap 保证连通性: 根据ac与ap设计好的ip配置,使之可以通讯 ac与ap可以实现跨网段管理 1、设置三层交换机的vlan 与vlanif信息 dhcp enable //开启dhcp ip pool forap //…...
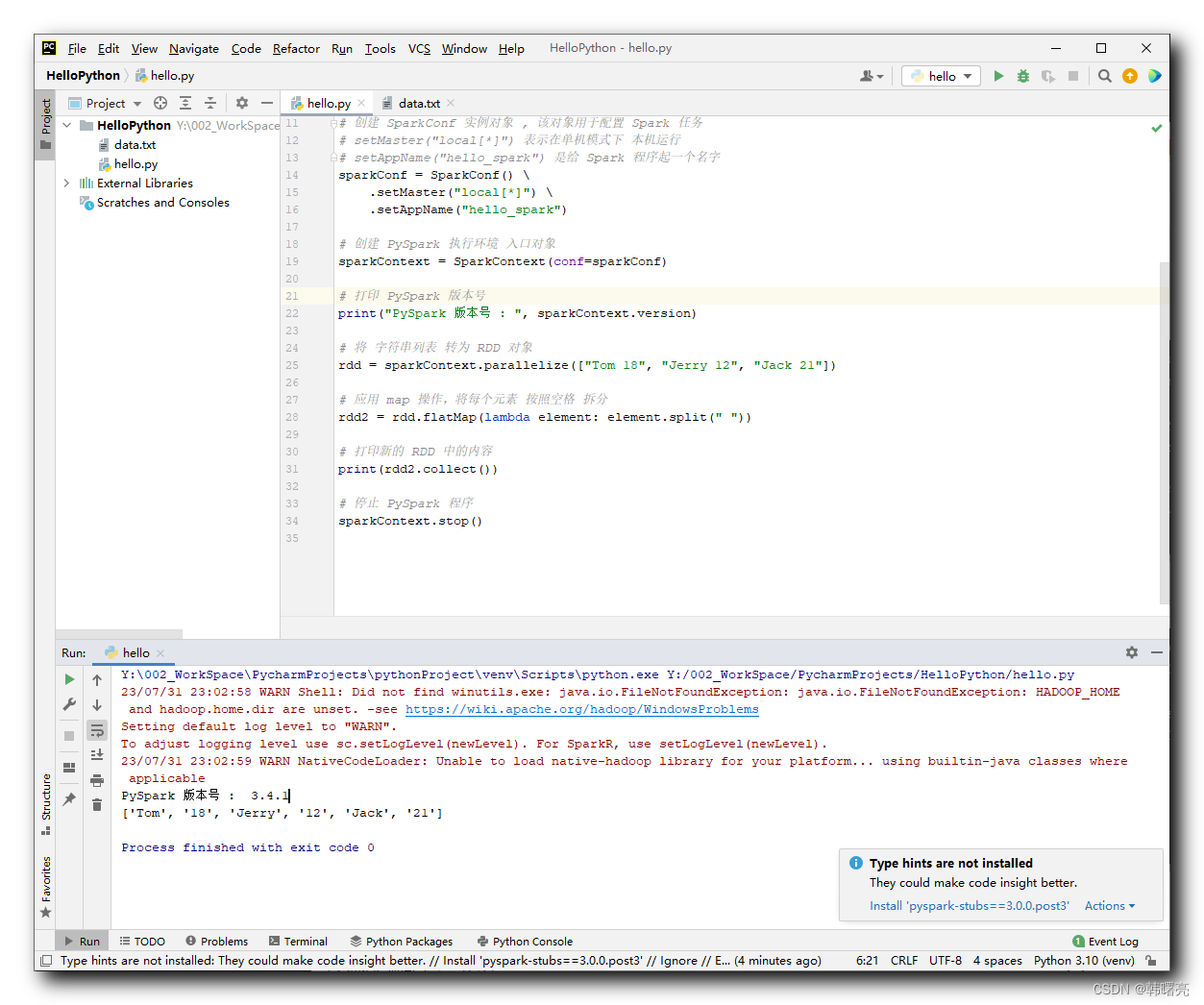
【Python】PySpark 数据计算 ② ( RDD#flatMap 方法 | RDD#flatMap 语法 | 代码示例 )
文章目录 一、RDD#flatMap 方法1、RDD#flatMap 方法引入2、解除嵌套3、RDD#flatMap 语法说明 二、代码示例 - RDD#flatMap 方法 一、RDD#flatMap 方法 1、RDD#flatMap 方法引入 RDD#map 方法 可以 将 RDD 中的数据元素 逐个进行处理 , 处理的逻辑 需要用外部 通过 参数传入 map…...
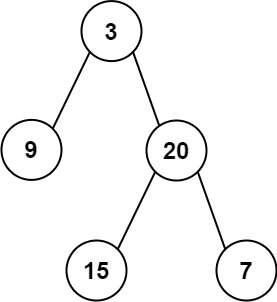
二叉树题目:左叶子之和
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:左叶子之和 出处:404. 左叶子之和 难度 3 级 题目描述 要求 给你二叉树的根结点 root \texttt{ro…...

Spark SQL报错: Task failed while writing rows.
错误 今天运行 Spark 任务时报了一个错误,如下所示: WARN scheduler.TaskSetManager: Lost task 9.0 in stage 3.0 (TID 69, xxx.xxx.xxx.com, executor 3): org.apache.spark.SparkException: Task failed while writing rows.at org.apache.spark.sq…...
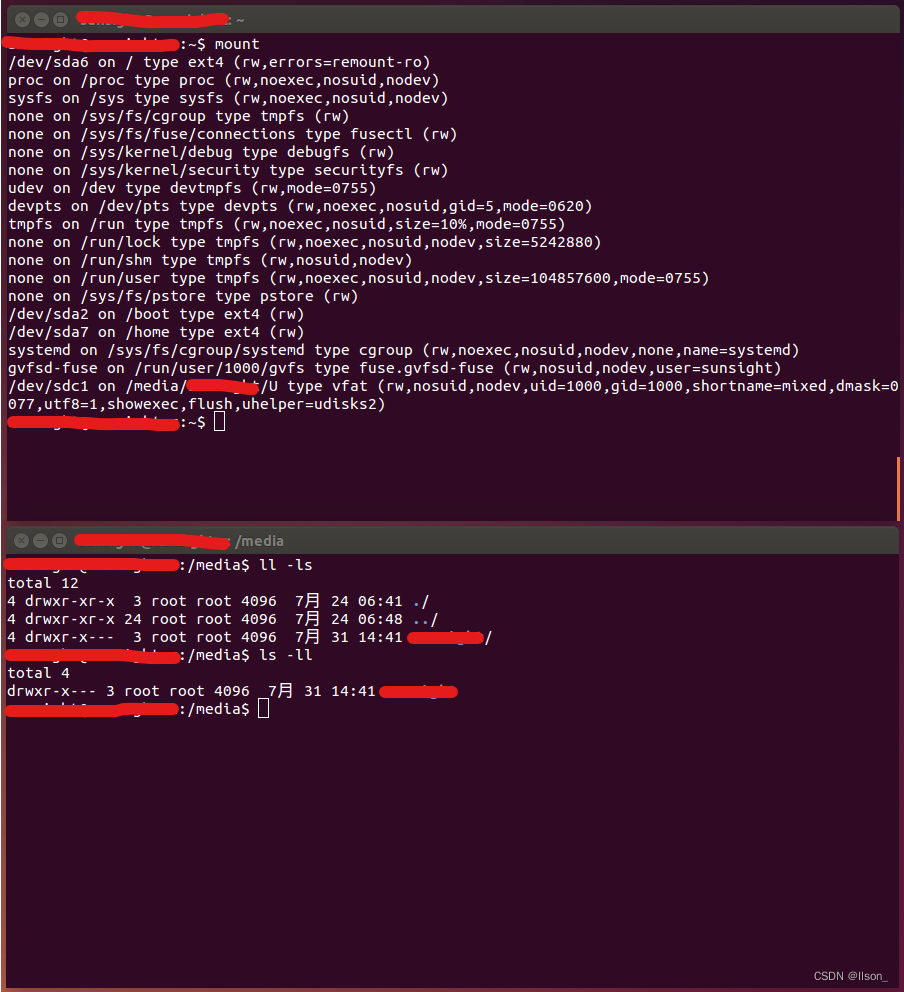
Linux系统下U盘打不开: No application is registered as handling this file
简述 系统是之前就安装好使用的Ubuntu14.04,不过由于某些原因只安装到了机械硬盘中;最近新买了一块固态硬盘,所以打算把Ubuntu系统迁移到新的固态硬盘上; 当成功的迁移了系统之后发现其引导有点问题,导致多个系统启动不…...

07 定时器处理非活动连接(上)
07 定时器处理非活动连接(上) 基础知识 非活跃,是指客户端(这里是浏览器)与服务器端建立连接后,长时间不交换数据,一直占用服务器端的文件描述符,导致连接资源的浪费。 定时事件&a…...
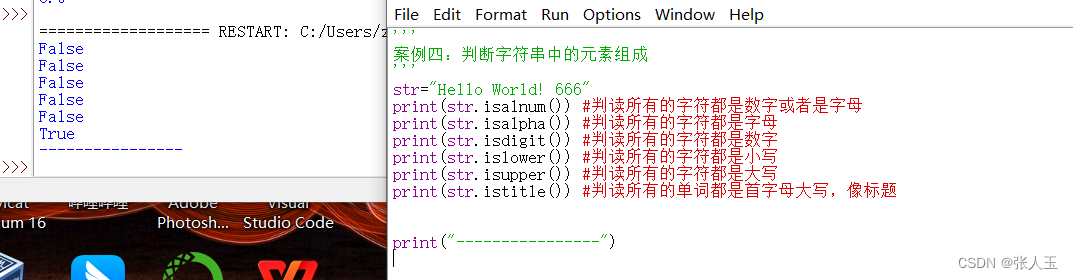
python——案例四:判断字符串中的元素组成
案例四:判断字符串中的元素组成str"Hello World! 666" print(str.isalnum()) #判读所有的字符都是数字或者是字母 print(str.isalpha()) #判读所有的字符都是字母 print(str.isdigit()) #判读所有的字符都是数字 print(str.islower()) #判读所有的字符都是…...
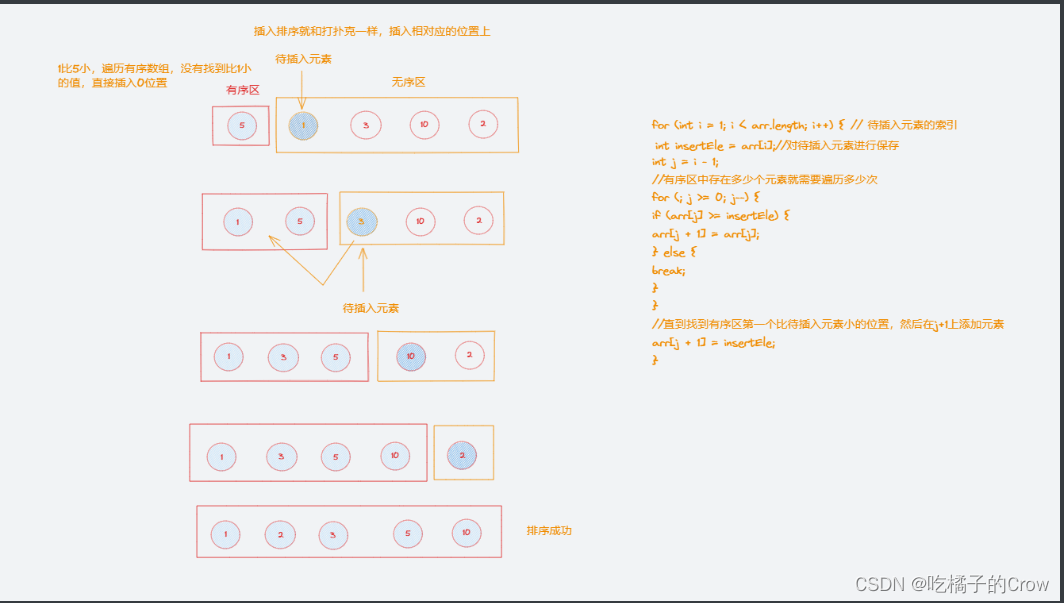
一起学算法(插入排序篇)
概念: 插入排序(inertion Sort)一般也被称为直接插入排序,是一种简单的直观的排序算法 工作原理:将待排列元素划分为(已排序)和(未排序)两部分,每次从&…...
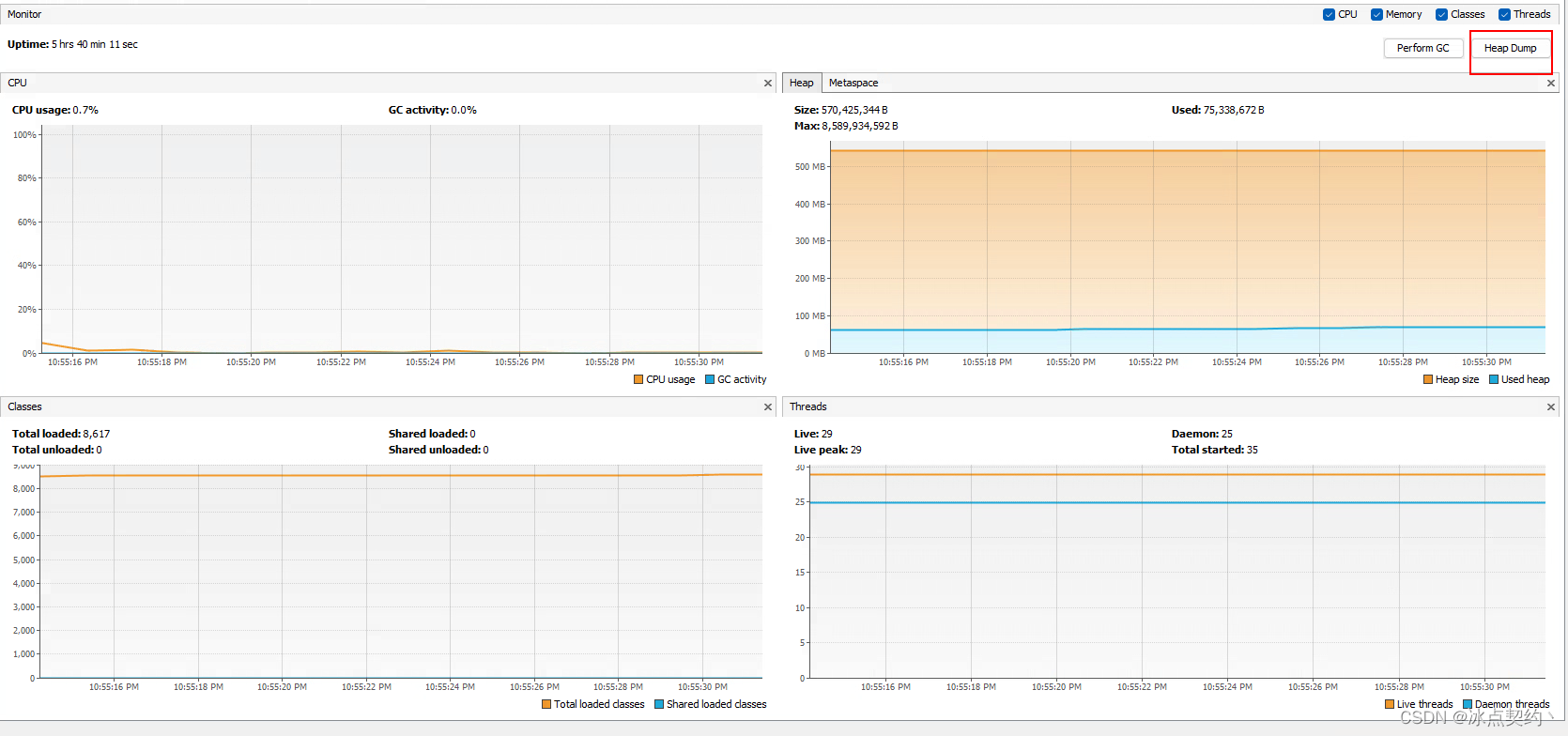
JVM基础篇-本地方法栈与堆
JVM基础篇-本地方法栈与堆 本地方法栈 什么是本地方法? 本地方法即那些不是由java层面实现的方法,而是由c/c实现交给java层面进行调用,这些方法在java中使用native关键字标识 public native int hashCode()本地方法栈的作用? 为本地方法提供内存空…...
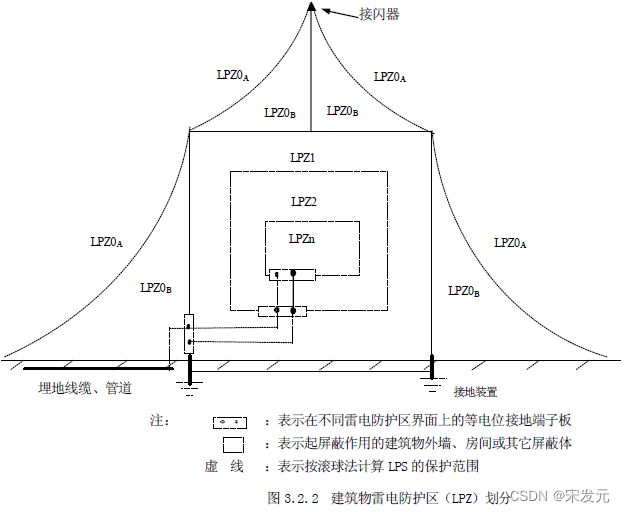
防雷保护区如何划分,防雷分区概念LPZ介绍
在防雷设计中,很重要的一点就是防雷分区的划分,只有先划分好防雷区域等级,才好做出比较好的防雷器设计方案。 因为标准对不同区安装的防雷浪涌保护器要求是不一样的。 那么,防雷保护区是如何划分的呢? 如上图所示&…...

随手笔记——3D−3D:ICP求解
随手笔记——3D−3D:ICP求解 使用 SVD 求解 ICP使用非线性优化来求解 ICP 原理参见 https://blog.csdn.net/jppdss/article/details/131919483 使用 SVD 求解 ICP 使用两幅 RGB-D 图像,通过特征匹配获取两组 3D 点,最后用 ICP 计算它们的位…...

Python调用各大机器翻译API大全
过去的二三年中,我一直关注的是机器翻译API在自动化翻译过程中的应用,包括采用CAT工具和Python编程语言来调用机器翻译API,然后再进行译后编辑,从而达到快速翻译的目的。 然而,我发现随着人工智能的发展,很…...

重生之我要学C++第六天
这篇文章的主要内容是const以及权限问题、static关键字、友元函数和友元类,希望对大家有所帮助,点赞收藏评论支持一下吧! 更多优质内容跳转: 专栏:重生之C启程(文章平均质量分93) 目录 const以及权限问题 1.const修饰…...

SpringBoot中ErrorPage(错误页面)的使用--【ErrorPage组件】
SpringBoot系列文章目录 SpringBoot知识范围-学习步骤–【思维导图知识范围】 文章目录 SpringBoot系列文章目录本系列校训 SpringBoot技术很多很多环境及工具:必要的知识深层一些的知识 上效果图在Spring Boot里使用ErrorPage还要注意的是 配套资源作业ÿ…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
