八大排序源码(含优化)
文章目录
- 1、直接插入排序
- 2、希尔排序
- 3、选择排序
- 4、冒泡排序
- 5、堆排序
- 6、快速排序
- 快速排序递归实现
- 霍尔法
- 挖坑法
- 前后指针法
- 快速排序小区间优化
- 快速排序非递归实现
- 7、归并排序
- 归并排序递归实现
- 归并排序非递归
- 8、计数排序
大家好,我是纪宁,这篇文章是关于八大排序的源代码,具体实现过程会在后续文章中介绍。
1、直接插入排序
时间复杂度O(N^2),原数据越有序,效率越高。
当原数据有序时,则时间复杂度为O(N)。原数据倒序时,时间复杂度为O(N^2)

void InsertSort(int* a, int n)//直接插入排序
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end+1];while (end >= 0){if (a[end] >tmp){a[end + 1] = a[end];}else{break;}end--;}a[end + 1] = tmp;}
}
2、希尔排序
时间复杂度:O(N^1.3) 空间复杂度:O(1)
希尔排序是插入排序的优化,整体思路是先预排序,使原数据更接近有序,等到gap==1时,就变成了直接插入排序。
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//gap也可以 /=2;奇特数字必须保证gap最后的值为1for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];}else{break;}end -= gap;}arr[end + gap] = tmp;}}
}
3、选择排序
时间复杂度:O(N^2) 空间复杂度:O(1)
每次选择一个最大或者最小的数,使其出现在正确的位置。

void SelectSort(int* a, int n)
{for (int j = 0; j < n; j++){int mini = j;int maxi= n - j-1;for (int i = j; i < n-j; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[mini], &a[j]);if (maxi == j){maxi = mini;//最大值如果在 j 这个位置的话,结果这个位置被换成了min 的值}Swap(&a[maxi], &a[n-1-j]);}
}
4、冒泡排序
时间复杂度:O(N^2) 空间复杂度:O(1)
思路最简单的排序,所有程序员的白月光!

void BubbleSort(int* a, int n)//冒泡排序
{for (int i = 0; i < n; i++){int ret = 0;//如果一趟后ret还等于0,说明数据已经有序for (int j = 0; j < n - i - 1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);ret = 1;}}if (ret == 0)break;}
}
5、堆排序
时间复杂度:O(N*logN) 空间复杂度:O(1)
建堆的时候可以采用向上调整和向下调整建堆,而排序的时候只能使用向下调整算法。
排升序建大堆,降序建小堆。
void Adjustup(int* a, int child)//向上调整
{int parent = (child - 1) / 2;while (parent >= 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void Adjustdown(int* a, int parent, int n)//向下调整
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}void HeapSort(int* arr, int sz)
{//第一步,建堆向上调整建堆//for (int i = 1; i < sz; i++)//{// Adjustup(arr, i); //}//向下调整建堆for (int i = (sz - 1) / 2; i >= 0; i--){Adjustdown(arr, i, sz - 1);}int end = sz - 1;while (end > 0){Swap(&arr[0], &arr[end]);Adjustdown(arr, 0, end);end--;}
}
6、快速排序
时间复杂度:O(N*logN) 空间复杂度:O(1)
快速排序递归实现
霍尔法

int QuickSortPart1(int*a,int left,int right)//霍尔版本
{int* Maxi = (&a[left], &a[right], &(a[(left + right) / 2]));//三数取中Swap(&a[left], Maxi);//换到最左边int key = a[left];int keyi = left;while (left<right){while (left<right && a[right]>=key){right--;}while (left < right && a[left] <= key){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);return left;
}
void QuickSort(int*arr, int begin, int end)
{if (begin >= end)//等于是只有一个数需要排,大于是没有数需要排{return;}int keyi = QuickSortPart1(arr, begin, end);/*int keyi = QuickSortPart2(arr, begin, end);int keyi = QuickSortPart3(arr, begin, end);*/QuickSort(arr, begin, keyi - 1);QuickSort(arr, keyi + 1, end);
}
挖坑法

int QuickSortPart2(int* arr, int left, int right)//挖坑法
{int* Maxi = (&arr[left], &arr[right], &(arr[(left + right) / 2]));Swap(&arr[left], Maxi);int holei = left;int hole = arr[left];while (left < right){while (left < right && arr[right] >= hole){right--;}arr[holei] = arr[right];holei = right;while (left < right && arr[left] <= hole){left++;}arr[holei] = arr[left];holei = left;}arr[holei] = hole;return left;
}
void QuickSort(int*arr, int begin, int end)
{if (begin >= end)//等于是只有一个数需要排,大于是没有数需要排{return;}/*int keyi = QuickSortPart1(arr, begin, end);*/int keyi = QuickSortPart2(arr, begin, end);/*int keyi = QuickSortPart3(arr, begin, end);*/QuickSort(arr, begin, keyi - 1);QuickSort(arr, keyi + 1, end);
}
前后指针法

int QuickSortPart3(int* a, int left, int right)//快排快慢指针
{int* Maxi = (&a[left], &a[right], &(a[(left + right) / 2]));Swap(&a[left], Maxi);int keyi = left;int prev = left;int cur = left+1;while (cur <= right){if (a[cur] < a[keyi]&& ++prev!= cur){Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev],&a[keyi]);return prev;
}void QuickSort(int*arr, int begin, int end)
{if (begin >= end)//等于是只有一个数需要排,大于是没有数需要排{return;}//*int keyi = QuickSortPart1(arr, begin, end);*///int keyi = QuickSortPart2(arr, begin, end);int keyi = QuickSortPart3(arr, begin, end);QuickSort(arr, begin, keyi - 1);QuickSort(arr, keyi + 1, end);
}
快速排序小区间优化
void QuickSort1(int* a, int begin, int end)
{if (begin >= end)return;// 小区间优化,小区间不再递归分割排序,降低递归次数if ((end - begin + 1) > 10){int keyi = PartSort3(a, begin, end);// [begin, keyi-1] keyi [keyi+1, end]QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);}else{InsertSort(a + begin, end - begin + 1);//直接插入排序}
}快速排序非递归实现
快排非递归要用栈来实现
void QuickSortNorn(int* a, int begin, int end)
{ST st;//创建数组栈STInit(&st);//初始化栈STPush(&st, end);//入栈STPush(&st, begin);//入栈while (!STEmpty(&st))//判空{int left = STTop(&st);//取栈顶数据STPop(&st);//出栈int right = STTop(&st);STPop(&st);int keyi = QuickSortPart1(a, left,right);if (keyi + 1 < right){STPush(&st, right);STPush(&st, keyi + 1);}if (keyi - 1 > left){STPush(&st, keyi - 1);STPush(&st, left);}}STDestroy(&st);//销毁栈
}
7、归并排序
时间复杂度:O(N*logN) 空间复杂度:O(N)
归并排序递归实现

void _MergeSortPart(int* a, int* tmp, int begin, int end)
{if (begin >= end)return;int midi = (begin + end) / 2;_MergeSortPart(a, tmp, begin, midi);_MergeSortPart(a, tmp, midi + 1, end);int begin1 = begin, end1 = midi;int begin2 = midi + 1, end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a+begin, tmp+begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);_MergeSortPart(a, tmp, 0, n - 1);free(tmp);tmp = NULL;
}
归并排序非递归
void _MergeSortNonr(int* a, int* tmp, int begin, int end)
{int gap = 1;while (gap <= end){for (int i = 0; i <= end; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = i;if (begin2 > end){break;}if (end2 > end){end2 = end;//对范围进行修正}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));//拷贝回原数组}gap *= 2;}}
void MergeSortNonr(int* a, int n)//归并排序非递归
{int* tmp = (int*)malloc(sizeof(int) * n);_MergeSortNonr(a, tmp, 0, n - 1);free(tmp);tmp = NULL;
}
8、计数排序
时间复杂度:O(MAX(N,range)) 空间复杂度:O(range)
void CountSort(int* a, int n)//计数排序
{//先找最大值和最小值int maxi = 0, mini = 0;for (int i = 1; i < n; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}int max = a[maxi], min = a[mini];int range = a[maxi] - a[mini]+1;int* count = (int*)malloc(sizeof(int) * range);memset(count, 0, sizeof(int) * range);for (int j = 0; j < n; j++){count[a[j] - min]++;}int i = 0;for (int j = 0; j < n; j++){while (count[j]--){ a[i++] = j + min;}}
}
相关文章:

八大排序源码(含优化)
文章目录 1、直接插入排序2、希尔排序3、选择排序4、冒泡排序5、堆排序6、快速排序快速排序递归实现霍尔法挖坑法前后指针法快速排序小区间优化 快速排序非递归实现 7、归并排序归并排序递归实现归并排序非递归 8、计数排序 大家好,我是纪宁,这篇文章是关…...

单调队列---数据结构与算法
简介 队列也是一种受限制的线性表和栈相类似,栈是先进后出,而队列是先进先出,就好像一没有底的桶,往里面放东西,如图 在这里也是用数组来实现队列,用数组实现的叫做顺序队列 队列的数组模拟 const int N…...

小程序如何使用自定义组件
使用自定义组件的步骤如下: 创建自定义组件:在小程序项目根目录下的 components 文件夹中创建一个文件夹,然后在该文件夹中创建一个 .json 文件、一个 .wxml 文件和一个 .js 文件,这三个文件分别对应组件的配置、模板和逻辑。 在…...

归并排序含非递归版
目录 1.归并排序的原理 2.实现归并排序 2.1框架 2.2区间问题和后序遍历 2.3归并并拷贝 2.4归并排序代码 2.5测试 3.非递归实现归并排序 3.1初次实现 3.2测试 3.3修改 3.4修改测试 1.归并排序的原理 归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治…...

项目进展(八)-编写代码,驱动ADS1285
一、代码 根据芯片的数据手册编写部分驱动,首先看部分引脚的波形: DRDY: CS: 首先在代码初始化时连续写入三个寄存器: void WriteReg(uint8_t startAddr, uint8_t *regData, uint8_t number) {uint8_t i0;// 循环写number1次…...
【MyBatis-Plus】快速精通Mybatis-plus框架—快速入门
大家在日常开发中应该能发现,单表的CRUD功能代码重复度很高,也没有什么难度。而这部分代码量往往比较大,开发起来比较费时。 因此,目前企业中都会使用一些组件来简化或省略单表的CRUD开发工作。目前在国内使用较多的一个组件就是…...

docker 安装kafka
运行容器 zookeeper: [rootk8s-master ~]# docker run -d --restartalways --log-driver json-file --log-opt max-size100m --log-opt max-file2 --name zookeeper -p 2181:2181 -v /etc/localtime:/etc/localtime zookeeper c603f292813cfd6e2b16fff88a9767cc86fc9bba34d82…...

容器内获得apiserver地址
1.容器的Env的KUBENETES_SERVICE_HOST字段 roottomcat01-69fc8f859b-w9btn:/tmp# env | grep KUBERNETES_SERVICE_HOST10.96.0.1 KUBERNETES_SERVICE_HOST10.96.0.12.通过域名查询 nslookup getent hosts roottomcat01-69fc8f859b-w9btn:/tmp# getent hosts kubernetes.def…...
)
linux服务端c++开发工具介绍(vscode版)
本文适合于有一定c开发经验,但是还不明确如何到linux服务端开发程序的同学。 一、vscode 几年前用的是ssh到云服务上,再用vim在云上开发的形式 ssh dongbeijing.dbj11.158.142.176 vim hello.c 现今,由于vscode比较好用,这几年…...

Linux常用命令大全
Linux常用命令大全 一、文件&目录管理1. 文件和目录操作命令2. 查看文件及内容处理命令3. 文件压缩及解压缩命令4. 搜索文件命令5. 其他 二、Linux 软件包管理三、用户管理1. 用户管理2. 查看系统用户登陆信息的命令 四、进程管理五、网络通信1. 基础网络操作命令2. 深入网…...

Python中取2023, 9, 1——2023, 10, 31的全部时间
使用datetime.date()函数定义了开始和结束日期。然后,我们使用datetime.timedelta()类创建了一个时间范围,其中n表示从开始日期到结束日期之间的天数。最后,我们使用一个for循环迭代时间范围内的日期,并打印每个日期。示例代码演示…...

创建django文件
1、在指定目录里打开终端,输入D:\Softwares\Anaconda3\envs\pytorch\Scripts\django-admin .exe startproject 名称 ,即可在对应目录里创建django文件。...
全排列[中等]
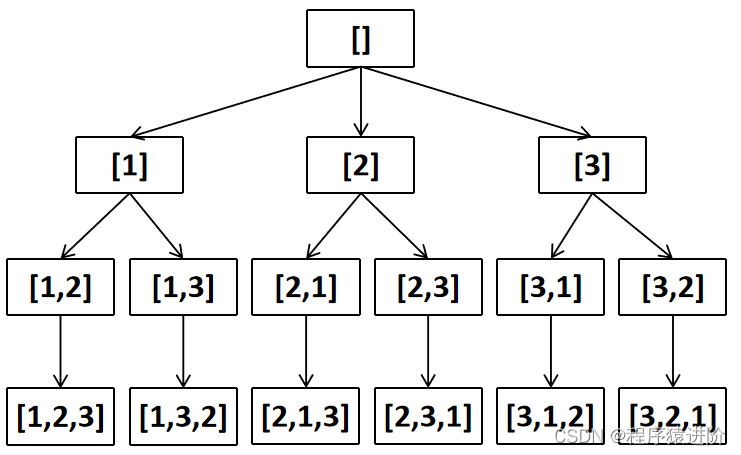
优质博文:IT-BLOG-CN 一、题目 给定一个不含重复数字的数组nums,返回其所有可能的全排列。你可以按任意顺序返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示例…...
mybatise-plus的id过长问题
一、问题情景 笔者在做mp插入数据库(id已设置为自增)操作时,发现新增数据的id过长,结果导致前端JS拿到的数据出现了精度丢失问题,原因是后端id的类型是Long。在网上查了一下,只要在该属性上加上如下注解就可以 TableId(value &q…...
图示矩阵分解
特征值与特征向量 设 A A A 是 n 阶矩阵,如果存在数 λ \lambda λ 和 n 维非零列向量 x x x,满足关系式: A x λ x ( 1 ) Ax \lambda x\quad\quad(1) Axλx(1) 则数 λ \lambda λ 称为矩阵 A A A 的特征值,非零向量 x…...
六、互联网技术——数据存储
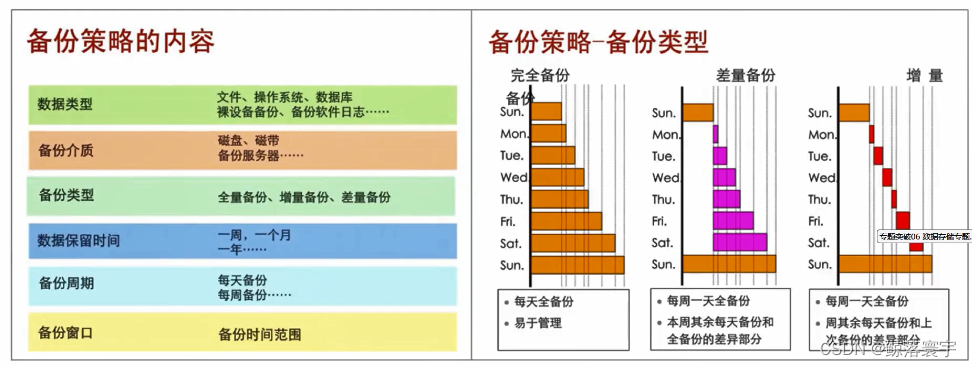
文章目录 一、存储系统层次结构二、按照重要性分类三、磁盘阵列RAID三、RAID基础四、磁盘阵列分级五、数据备份与恢复六、容灾与灾难恢复 一、存储系统层次结构 常见的三层存储体系结构如下图所示,分为高速缓冲存储器、主存储器和外存储器。 二、按照重要性分类 …...

六、vpp 流表+负载均衡
草稿!!! vpp node其实就是三个部分 1、plugin init 2、set command 3、function 实现功能,比如这里的流表 今天我们再用VPP实现一个流表的功能 一、流表 1.1流表----plugin init VLIB_REGISTER_NODE 注册流表节点 // 注册流…...
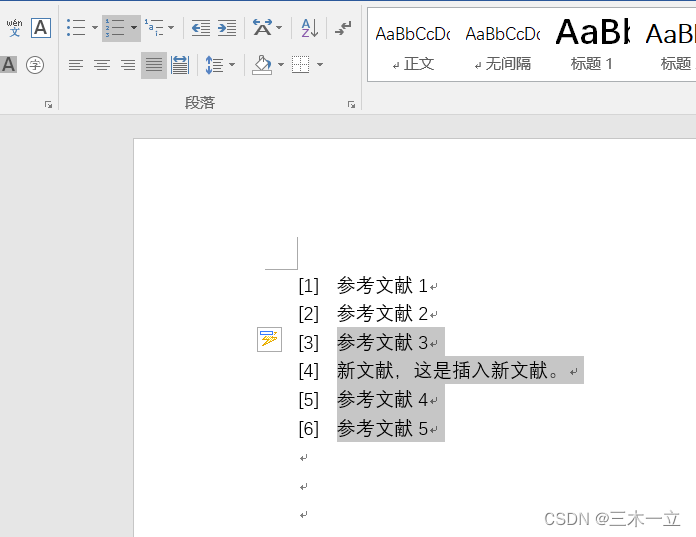
word已排序好的参考文献,插入新的参考文献,序号更新
原排序好的文献序号。 现在在3号后面插入一个新文献。4,5号应该成为5,6 这时在3号后面,回车,就会自动的增长。如下图: 但是如果手滑,把[4]删除了如何排序?? 如下图: …...
二叉树的顺序存储——堆——初识堆排序
前面我们学过可以把完全二叉树存入到顺序表中,然后利用完全二叉树的情缘关系,就可以通过数组下标来联系。 但是并不是把二叉树存入到数组中就是堆了,要看原原来的二叉树是否满足:所有的父都小于等于子,或者所有的父都…...

CYEZ 模拟赛 9
A a ⊥ b ⇒ a − b ⊥ a b (1) a \perp b \Rightarrow a-b \perp ab \tag {1} a⊥b⇒a−b⊥ab(1) 证明: gcd ( a , b ) gcd ( b , a − b ) \gcd(a,b) \gcd(b, a-b) gcd(a,b)gcd(b,a−b),故 a − b ⊥ b a - b \perp b a−b⊥b,同…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...
