<a>标签的download属性部分浏览器无法自动识别文件后缀
问题
最近开发中遇到的问题,文件名中含有点和逗号字符,当使用a标签的download属性下载内容时,如果不指定后缀,部分浏览器无法自动识别文件后缀。如下图所示:

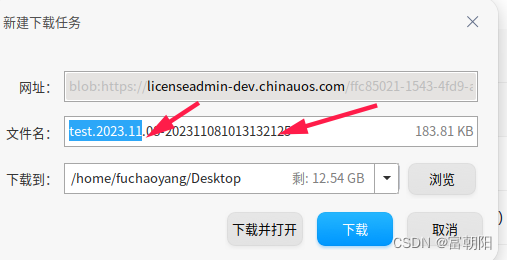
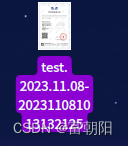
定义用法
download 属性定义了下载链接的地址。
href 属性必须在 标签中指定。
属性同样可以指定下载文件的名称。
文件名称没有限定值,浏览器会自动在文件名称末尾添加该下载文件的后缀 (.img, .pdf, .txt, .html, 等),添加后缀将使用指定后缀,不会重复出现。
案例:
function downloadData(){// 使用a的download属性下载文件let filename = '文件名称';let data = '数据';let blob = new Blob([data],{type:'application/vnd.ms-excel'})let a = document.createElement('a');//创建a元素a.href = URL.createObjectURL(blob);a.download = filename;a.click();//触发a的点击事件//URL.revokeObjectUrl(a.href)a = null;
}解决方案
注意当使用download属性实现下载时要添加后缀!!!
downloadRenewal(data) {const id = data.renewal_id;this.http.post(this.commonApiService.apiList.apis.license_in.renewalCertificateDownload, { id }).subscribe((res) => {if (res.code !== 0) {this.msg.error(res.msg)return} else {fetch(res.row.download_url).then(res => res.blob().then(blob => {const a = document.createElement('a'),url = window.URL.createObjectURL(blob),// 强行指定文件后缀filename = `${data.renewal_order_name}-${data.order_no}.pdf`;a.href = url;a.download = filename;console.log(a)a.click();window.URL.revokeObjectURL(url);}));}})}兼容性(浏览器支持)

问题完美解决,YYDS! 欢迎在评论区交流。
如果文章对你有所帮助,❤️关注+点赞❤️鼓励一下!博主会持续更新。。。。
相关文章:

<a>标签的download属性部分浏览器无法自动识别文件后缀
问题 最近开发中遇到的问题,文件名中含有点和逗号字符,当使用a标签的download属性下载内容时,如果不指定后缀,部分浏览器无法自动识别文件后缀。如下图所示: 定义用法 download 属性定义了下载链接的地址。 href 属性…...

前端图片压缩上传,减少等待时间!优化用户体检
添加图片注释,不超过 140 字(可选) 这里有两张图片,它们表面看上去是一模一样的,但实际上各自所占用的内存大小相差了180倍。 添加图片注释,不超过 140 字(可选) 添加图片注释&…...

Ionic header content footer toolbar UI实例
1 ionic的button图标 <ion-header [translucent]"true"><ion-toolbar><ion-buttons slot"start"><ion-back-button default-href"/tabs/tab1" text"back" icon"caret-back"></ion-back-button&…...
uniapp 解决H5跨域的问题
uniapp 解决h5跨域问题 manifest.json manifest.json文件中,点击“源码视图”,在此对象的最后添加以下代码: "h5" : {"devServer" : {"port" : 8080, //端口号"disableHostCheck" : true,"proxy" :…...
对称加密(symmetric encryption)和非对称加密(Asymmetric Encryption)(密钥、公钥加密、私钥解密)AES、RSA
文章目录 对称加密与非对称加密对称加密1.1 定义1.2 工作原理1.3 场景分析1.4 算法示例(以AES为例)1.5 对称加密的优点与缺点优点缺点 非对称加密2.1 定义2.2 工作原理注意:每次生成的RSA密钥对都会不一样 2.3 场景分析2.4 算法示例ÿ…...
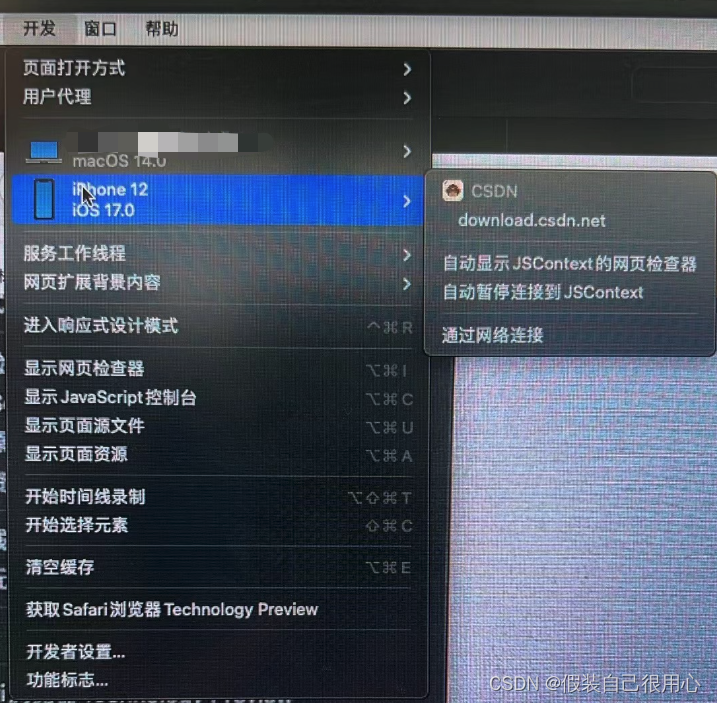
iOS 16.4 之后真机与模拟器无法使用Safari调试H5页面问题
背景 iOS 16.4之后用真机调试H5时候发现,Safari中开发模块下面无法调试页面 解决方案 在WKWebView中设置以下代码解决 if (available(iOS 16.4, *)) {[_webView setInspectable:YES];}然后再次调试就可以了...
野火霸天虎 STM32F407 学习笔记_3 尝试寄存器映射方式点亮 LED 灯
新建工程 寄存器方式 要命啊,一看名字我就不想试。寄存器新建不得麻烦死。 哎算了为了学习原理,干了。 我们尝试自己写一个寄存器的库函数来引用。 首先我们需要引用 st 官方启动文件 stmf4xx.s,具体用途后面章节再展开讲解。然后我们自…...
ZZ308 物联网应用与服务赛题第F套
2023年全国职业院校技能大赛 中职组 物联网应用与服务 任 务 书 (F卷) 赛位号:______________ 竞赛须知 一、注意事项 1.检查硬件设备、电脑设备是否正常。检查竞赛所需的各项设备、软件和竞赛材料等; 2.竞赛任务中所使用…...

怎样选择文件外发控制系统,让数据实现高效安全交换?
制造型企业都非常重视其知识产权(IP)的安全性,尤其是其最有价值的产品设计数据的安全问题。基于复杂的供应链生态,每天可能要与几十家甚至上百家供应商及合作伙伴进行数据交换。不管是一级还是二级供应商,合作伙伴还是…...

专访 SPACE ID:通往 Web3 无许可域名服务协议之路
Web3 行业发展风起云涌,对于初创项目而言,如何寻找适合自己的赛道是首要问题。当前伴随用户交互和跨平台操作需求日渐兴起,如何更迅速地使用一站式域名实现便捷验证成为大众的心头期盼。 这一背景下,SPACE ID 于众星林立的 Web3 …...

合并分支--将自己的分支合并到master分支
在版本控制系统(例如Git)中,将自己的分支合并到master(或者主分支)通常需要以下步骤: ### 1. 切换到主分支 首先,确保你的本地仓库当前处于主分支。你可以使用以下命令切换到主分支࿱…...
)
力扣:153. 寻找旋转排序数组中的最小值(Python3)
题目: 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]若旋转…...
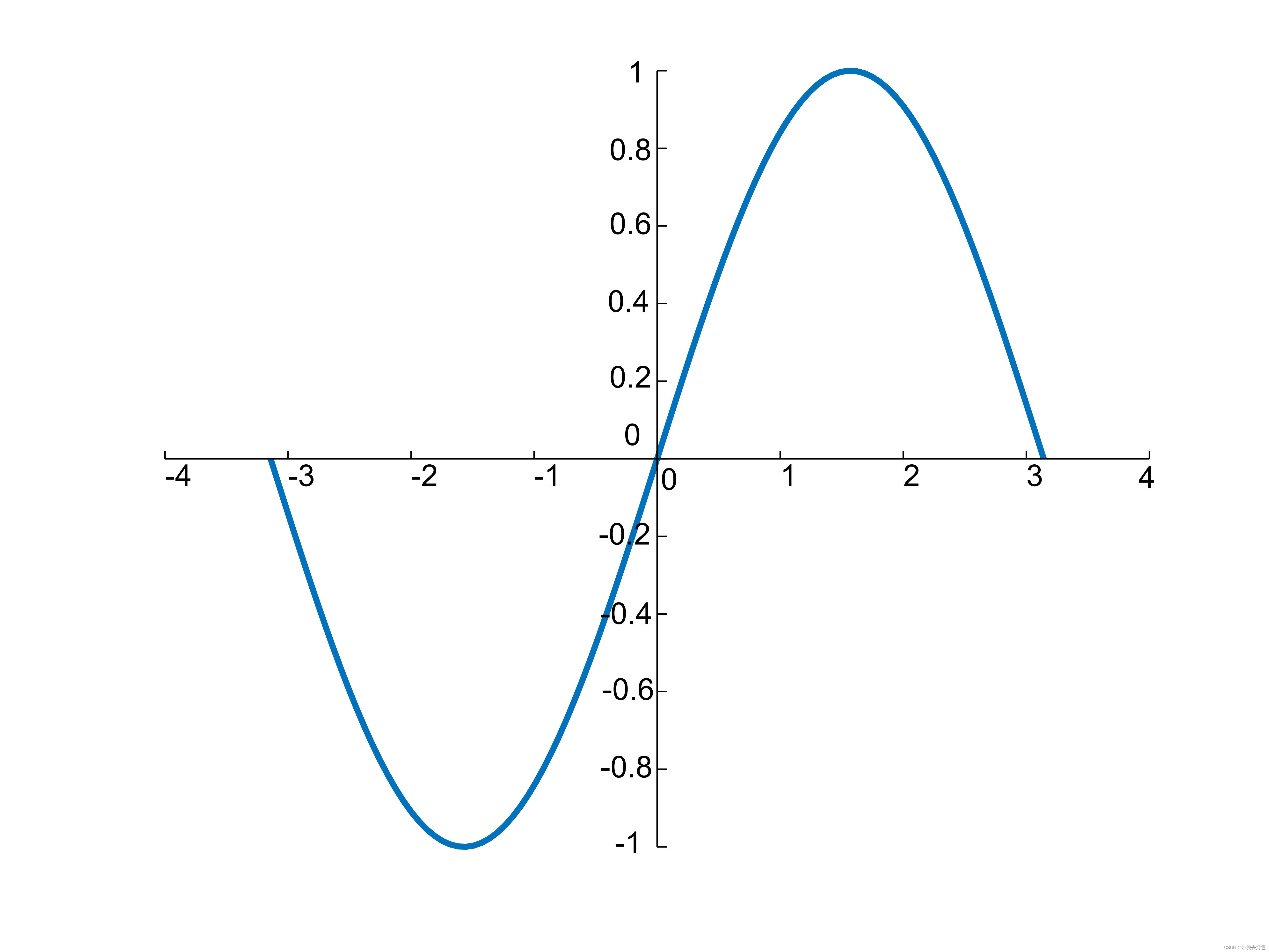
matlab中实现画函数图像添加坐标轴
大家好,我是带我去滑雪! 主函数matlab代码: function PlotAxisAtOrigin(x,y); if nargin 2 plot(x,y);hold on; elsedisplay( Not 2D Data set !) end; Xget(gca,Xtick); Yget(gca,Ytick); XLget(gca,XtickLabel); YLget(gca,YtickLabel)…...
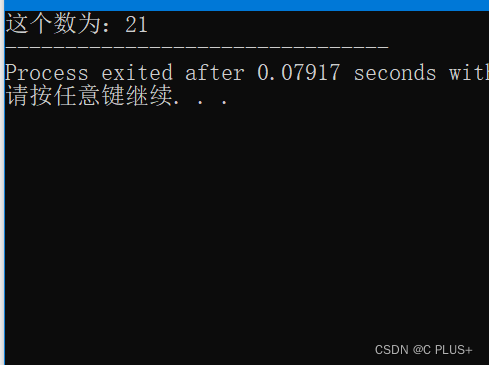
C语言求解一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
完整代码: /* 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问 该数是多少?*/ #include<stdio.h>int main(){//num为最终所求那个数int num;//i*i为第一个完全平方数for (int i 10; …...

AtCoder abc148
C题 求GCD D题 顺序遍历 E题 trailing zero只与5的个数有关,因此算一下5/25/125…的倍数 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.py # software : PyCharmimport bisect import copy import sys from itertools import perm…...

k8s、docker 卸载
k8s卸载 k8s 重置 kubeadm reset -f如果kubernets是1.24以上版本,请先单独卸载containerd sudo apt purge containerd.iok8s软件卸载 ubuntu #apt卸载 apt purge kubelet kubeadm kubectlcentos yum erase -y kubelet kubectl kubeadm 删除kubelet相关信息&am…...
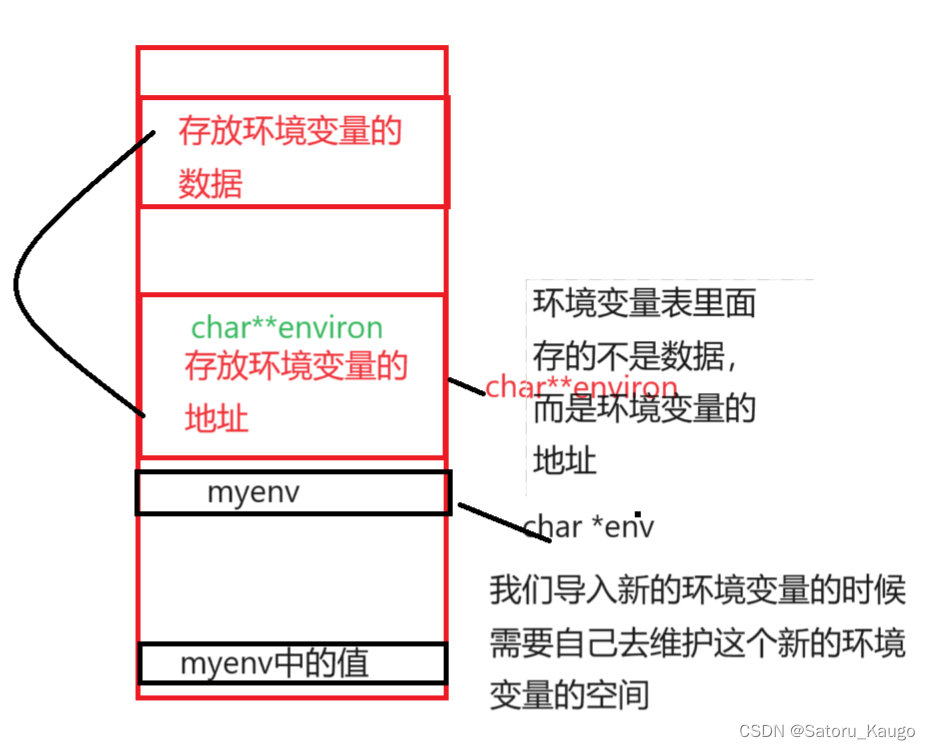
【Linux】Shell命令行的简易实现(C语言实现)内键命令,普通命令
文章目录 0.准备工作1.大体框架 一、获取命令行二、解析命令行三、进程执行1.普通命令2.内建命令 四、完整代码: 0.准备工作 1.大体框架 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <assert.h> #include <u…...
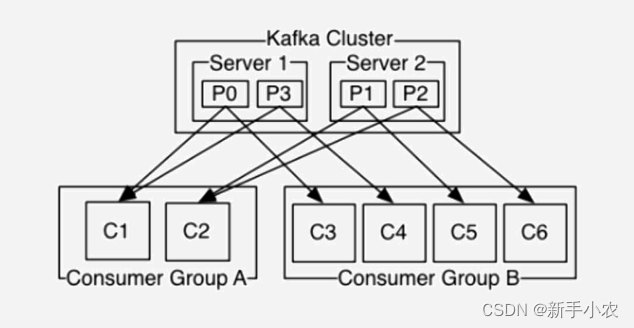
Kafka -- 架构、分区、副本
1、Kafka的架构: 1、producer:消息的生产者 2、consumer:消息的消费者 3、broker:kafka集群的服务者,一个broker就是一个节点,主要是负责处理消息的读、写的请求和存储消息。在kafka cluster中包含很多的br…...

CSS特效001:鼠标放div上,实现旋转、放大、移动等效果
GPT能够很好的应用到我们的代码开发中,能够提高开发速度。你可以利用其代码,做出一定的更改,然后实现效能。 css实战中,经常会看到这样的场景,鼠标放到一个图片或者一个div块状时候,会出现旋转、放大、移动…...

gin 快速入门手册
文章目录 安装URL和路由分组2. 带参数的url3. 获取路由分组的参数 获取参数1. 获取get参数2. 获取post参数3. get、post混合 JSON 、 ProtoBuf渲染1. 输出json和protobuf2. PureJSON 表单验证1. 表单的基本验证 中间件和next函数1. 无中间件启动2. 使用中间件3. 自定义组件 设置…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
