第三章:人工智能深度学习教程-基础神经网络(第一节-ANN 和 BNN 的区别)
你有没有想过建造大脑之类的东西是什么感觉,这些东西是如何工作的,或者它们的作用是什么?让我们看看节点如何与神经元通信,以及人工神经网络和生物神经网络之间有什么区别。
1.人工神经网络:人工神经网络(ANN)是一种基于前馈策略的神经网络。之所以这样称呼,是因为它们不断地通过节点传递信息,直到到达输出节点。这也被称为最简单的神经网络类型。ANN 的一些优点:
-
无论数据类型如何(线性或非线性),都能够学习。
-
人工神经网络具有高度波动性,最适合金融时间序列预测。
ANN 的一些缺点:
-
最简单的架构很难解释网络的行为。
-
该网络依赖于硬件。
2.生物神经网络:生物神经网络(BNN)是由突触、树突、细胞体和轴突组成的结构。在这个神经网络中,处理是由神经元进行的。树突接收来自其他神经元的信号,体细胞将所有输入信号相加,轴突将信号传输到其他细胞。
BNN 的一些优点:
-
突触是输入处理元件。
-
它能够处理高度复杂的并行输入。
BNN 的一些缺点:
-
没有控制机制。
-
处理速度很慢,因为它很复杂。
ANN 和 BNN 之间的区别:
生物神经网络(BNN)和人工神经网络(ANN)都由相似的基本组件组成,但它们之间也存在一些差异。
神经元:在 BNN 和 ANN 中,神经元是处理和传输信息的基本构建块。然而,BNN 神经元比 ANN 更复杂、更多样化。在 BNN 中,神经元具有多个树突,接收来自多个源的输入,轴突将信号传输到其他神经元,而在 ANN 中,神经元被简化,通常只有一个输出。
突触:在 BNN 和 ANN 中,突触是神经元之间的连接点,信息在此处传输。然而,在ANN中,神经元之间的连接通常是固定的,连接的强度由一组权重决定,而在BNN中,神经元之间的连接更加灵活,连接的强度可以通过多种因素,包括学习和经验。
神经通路:在 BNN 和 ANN 中,神经通路是神经元之间的连接,允许信息在整个网络中传输。然而,在 BNN 中,神经通路高度复杂且多样,神经元之间的连接可以通过经验和学习来修改。在人工神经网络中,神经通路通常更简单,并且由网络架构预先确定。
| 参数 | 神经网络 | 神经网络 |
| 结构 | 输入 重量 输出 隐藏层 | 树突 突触 轴突 细胞体 |
| 学习 | 非常精确的结构和格式化数据 | 他们可以容忍歧义 |
| 处理器 | 复杂的 高速 一个或几个 | 简单的 低速 大数字 |
| 记忆 | 与处理器分离 本地化的 非内容可寻址 | 集成到处理器中 分散式 内容可寻址 |
| 计算 | 集中 顺序的 存储程序 | 分散式 平行线 自学 |
| 可靠性 | 非常脆弱 | 强壮的 |
| 专业知识 | 数字和符号 操纵 | 感性的 问题 |
| 操作环境 | 明确的 良好约束的 | 定义不清 无约束的 |
| 容错能力 | 容错潜力 | 即使部分损坏,性能也会下降 |
总体而言,虽然 BNN 和 ANN 共享许多基本组件,但它们在复杂性、灵活性和适应性方面存在显着差异。BNN 是高度复杂且适应性强的系统,可以并行处理信息,其可塑性使它们能够随着时间的推移进行学习和适应。相比之下,人工神经网络是更简单的系统,旨在执行特定任务,它们的连接通常是固定的,网络架构由设计者确定。
相关文章:
)
第三章:人工智能深度学习教程-基础神经网络(第一节-ANN 和 BNN 的区别)
你有没有想过建造大脑之类的东西是什么感觉,这些东西是如何工作的,或者它们的作用是什么?让我们看看节点如何与神经元通信,以及人工神经网络和生物神经网络之间有什么区别。 1.人工神经网络:人工神经网络(…...

高防CDN与高防服务器:为什么高防服务器不能完全代替高防CDN
在当今的数字化时代,网络安全已经成为企业不容忽视的关键问题。面对不断增长的网络威胁和攻击,许多企业采取了高防措施以保护其网络和在线资产。然而,高防服务器和高防CDN是两种不同的安全解决方案,各自有其优势和局限性。在本文中…...
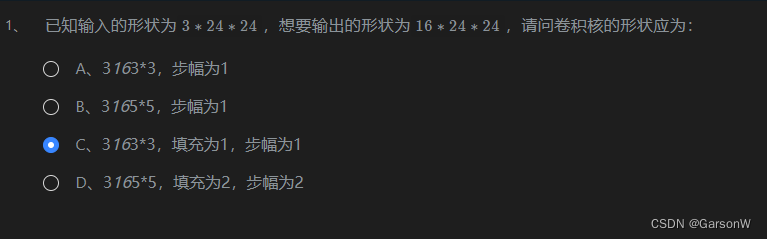
关于卷积神经网络的多通道
多通道输入 当输入的数据包含多个通道时,我们需要构造一个与输入通道数相同通道数的卷积核,从而能够和输入数据做卷积运算。 假设输入的形状为n∗n,通道数为ci,卷积核的形状为f∗f,此时,每一个输入通道都…...

19、Flink 的Table API 和 SQL 中的内置函数及示例(1)
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...

<a>标签的download属性部分浏览器无法自动识别文件后缀
问题 最近开发中遇到的问题,文件名中含有点和逗号字符,当使用a标签的download属性下载内容时,如果不指定后缀,部分浏览器无法自动识别文件后缀。如下图所示: 定义用法 download 属性定义了下载链接的地址。 href 属性…...

前端图片压缩上传,减少等待时间!优化用户体检
添加图片注释,不超过 140 字(可选) 这里有两张图片,它们表面看上去是一模一样的,但实际上各自所占用的内存大小相差了180倍。 添加图片注释,不超过 140 字(可选) 添加图片注释&…...

Ionic header content footer toolbar UI实例
1 ionic的button图标 <ion-header [translucent]"true"><ion-toolbar><ion-buttons slot"start"><ion-back-button default-href"/tabs/tab1" text"back" icon"caret-back"></ion-back-button&…...
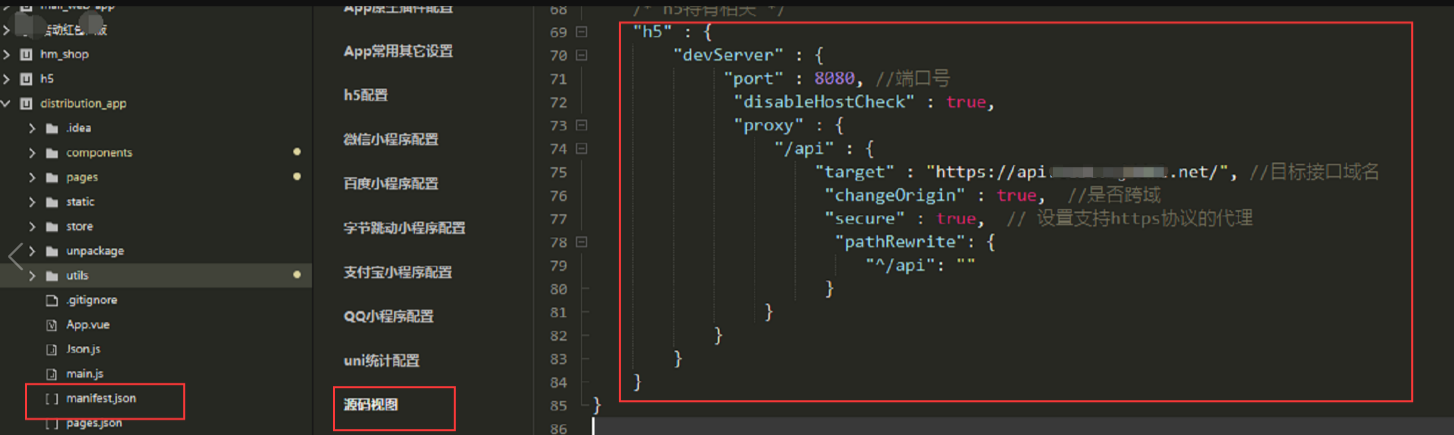
uniapp 解决H5跨域的问题
uniapp 解决h5跨域问题 manifest.json manifest.json文件中,点击“源码视图”,在此对象的最后添加以下代码: "h5" : {"devServer" : {"port" : 8080, //端口号"disableHostCheck" : true,"proxy" :…...
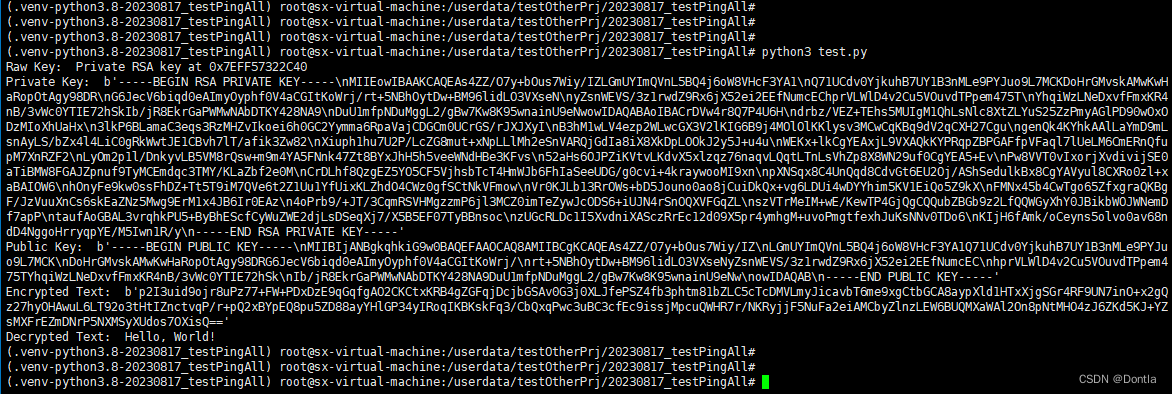
对称加密(symmetric encryption)和非对称加密(Asymmetric Encryption)(密钥、公钥加密、私钥解密)AES、RSA
文章目录 对称加密与非对称加密对称加密1.1 定义1.2 工作原理1.3 场景分析1.4 算法示例(以AES为例)1.5 对称加密的优点与缺点优点缺点 非对称加密2.1 定义2.2 工作原理注意:每次生成的RSA密钥对都会不一样 2.3 场景分析2.4 算法示例ÿ…...
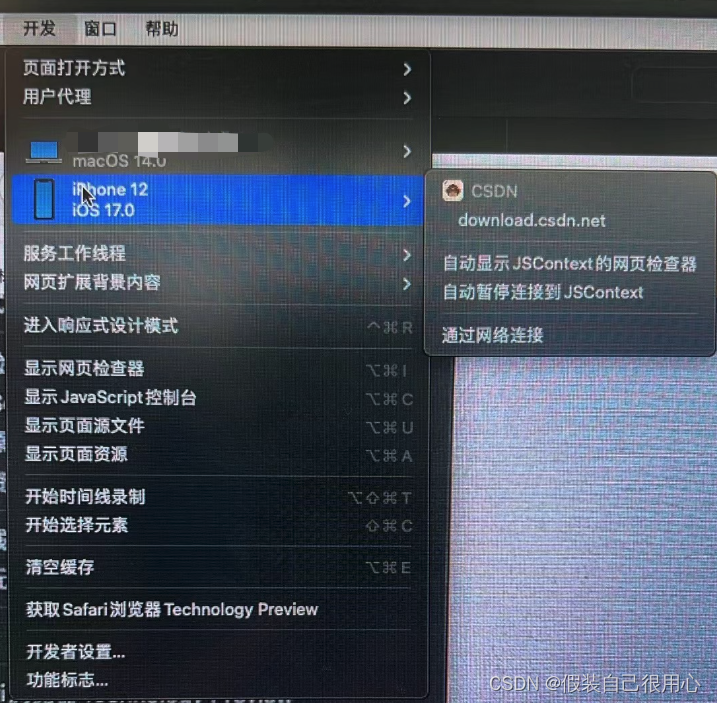
iOS 16.4 之后真机与模拟器无法使用Safari调试H5页面问题
背景 iOS 16.4之后用真机调试H5时候发现,Safari中开发模块下面无法调试页面 解决方案 在WKWebView中设置以下代码解决 if (available(iOS 16.4, *)) {[_webView setInspectable:YES];}然后再次调试就可以了...
野火霸天虎 STM32F407 学习笔记_3 尝试寄存器映射方式点亮 LED 灯
新建工程 寄存器方式 要命啊,一看名字我就不想试。寄存器新建不得麻烦死。 哎算了为了学习原理,干了。 我们尝试自己写一个寄存器的库函数来引用。 首先我们需要引用 st 官方启动文件 stmf4xx.s,具体用途后面章节再展开讲解。然后我们自…...
ZZ308 物联网应用与服务赛题第F套
2023年全国职业院校技能大赛 中职组 物联网应用与服务 任 务 书 (F卷) 赛位号:______________ 竞赛须知 一、注意事项 1.检查硬件设备、电脑设备是否正常。检查竞赛所需的各项设备、软件和竞赛材料等; 2.竞赛任务中所使用…...

怎样选择文件外发控制系统,让数据实现高效安全交换?
制造型企业都非常重视其知识产权(IP)的安全性,尤其是其最有价值的产品设计数据的安全问题。基于复杂的供应链生态,每天可能要与几十家甚至上百家供应商及合作伙伴进行数据交换。不管是一级还是二级供应商,合作伙伴还是…...

专访 SPACE ID:通往 Web3 无许可域名服务协议之路
Web3 行业发展风起云涌,对于初创项目而言,如何寻找适合自己的赛道是首要问题。当前伴随用户交互和跨平台操作需求日渐兴起,如何更迅速地使用一站式域名实现便捷验证成为大众的心头期盼。 这一背景下,SPACE ID 于众星林立的 Web3 …...

合并分支--将自己的分支合并到master分支
在版本控制系统(例如Git)中,将自己的分支合并到master(或者主分支)通常需要以下步骤: ### 1. 切换到主分支 首先,确保你的本地仓库当前处于主分支。你可以使用以下命令切换到主分支࿱…...
)
力扣:153. 寻找旋转排序数组中的最小值(Python3)
题目: 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]若旋转…...
matlab中实现画函数图像添加坐标轴
大家好,我是带我去滑雪! 主函数matlab代码: function PlotAxisAtOrigin(x,y); if nargin 2 plot(x,y);hold on; elsedisplay( Not 2D Data set !) end; Xget(gca,Xtick); Yget(gca,Ytick); XLget(gca,XtickLabel); YLget(gca,YtickLabel)…...
C语言求解一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
完整代码: /* 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问 该数是多少?*/ #include<stdio.h>int main(){//num为最终所求那个数int num;//i*i为第一个完全平方数for (int i 10; …...

AtCoder abc148
C题 求GCD D题 顺序遍历 E题 trailing zero只与5的个数有关,因此算一下5/25/125…的倍数 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.py # software : PyCharmimport bisect import copy import sys from itertools import perm…...

k8s、docker 卸载
k8s卸载 k8s 重置 kubeadm reset -f如果kubernets是1.24以上版本,请先单独卸载containerd sudo apt purge containerd.iok8s软件卸载 ubuntu #apt卸载 apt purge kubelet kubeadm kubectlcentos yum erase -y kubelet kubectl kubeadm 删除kubelet相关信息&am…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
