剑指 Offer II 017. 含有所有字符的最短字符串
题目链接
剑指 Offer II 017. 含有所有字符的最短字符串 hard
题目描述
给定两个字符串 s和 t。返回 s中包含 t的所有字符的最短子字符串。如果 s中不存在符合条件的子字符串,则返回空字符串 ""。
如果 s中存在多个符合条件的子字符串,返回任意一个。
注意: 对于 t中重复字符,我们寻找的子字符串中该字符数量必须不少于 t中该字符数量。
示例 1:
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
解释:最短子字符串 “BANC” 包含了字符串 t 的所有字符 ‘A’、‘B’、‘C’
示例 2:
输入:s = “a”, t = “a”
输出:“a”
示例 3:
输入:s = “a”, t = “aa”
输出:“”
解释:t 中两个字符 ‘a’ 均应包含在 s 的子串中,因此没有符合条件的子字符串,返回空字符串。
提示:
- 1<=s.length,t.length<=1051 <= s.length, t.length <= 10^51<=s.length,t.length<=105
s和t由英文字母组成
分析:
本题用 滑动窗口 求解。
用哈希表 ht记录 t中字符的出现次数。
再用另一个哈希表 hs记录 s滑动窗口区间的字符出现次数。
用两个指针 i和 j分别维护滑动窗口的左边界 和 右边界。
如果 hs[s[j]] <= ht[s[j]],说明此时的 s[j]依旧是有效字符,区间有效字符数 cnt += 1。
如果 hs[s[i]] > ht[s[i]],说明此时的区间内部字符已经超过了 t,所以收缩左区间,hs[s[i]]--,i++。
如果 cnt == t.size(),说明此时的区间 [l,r]包含了 t的所有字符,所以此时的 s.substr(i,j-i+1)可作为答案之一。
时间复杂度: O(n)O(n)O(n)
代码:
class Solution {
public:string minWindow(string s, string t) {int m = s.size() , n = t.size();if(m < n) return "";unordered_map<char,int> ht,hs;for(auto &c:t) ht[c]++;int len = 1e9,idx = -1;int cnt = 0;for(int i = 0,j = 0;j < m;j++){hs[s[j]]++;if(hs[s[j]] <= ht[s[j]]) cnt++;while(hs[s[i]] > ht[s[i]]){hs[s[i]]--;i++;}if(cnt == n){if(j - i + 1 < len){idx = i;len = j - i + 1;}}}return idx == -1 ? "" : s.substr(idx,len);}
};
相关文章:

剑指 Offer II 017. 含有所有字符的最短字符串
题目链接 剑指 Offer II 017. 含有所有字符的最短字符串 hard 题目描述 给定两个字符串 s和 t。返回 s中包含 t的所有字符的最短子字符串。如果 s中不存在符合条件的子字符串,则返回空字符串 ""。 如果 s中存在多个符合条件的子字符串,返回任…...
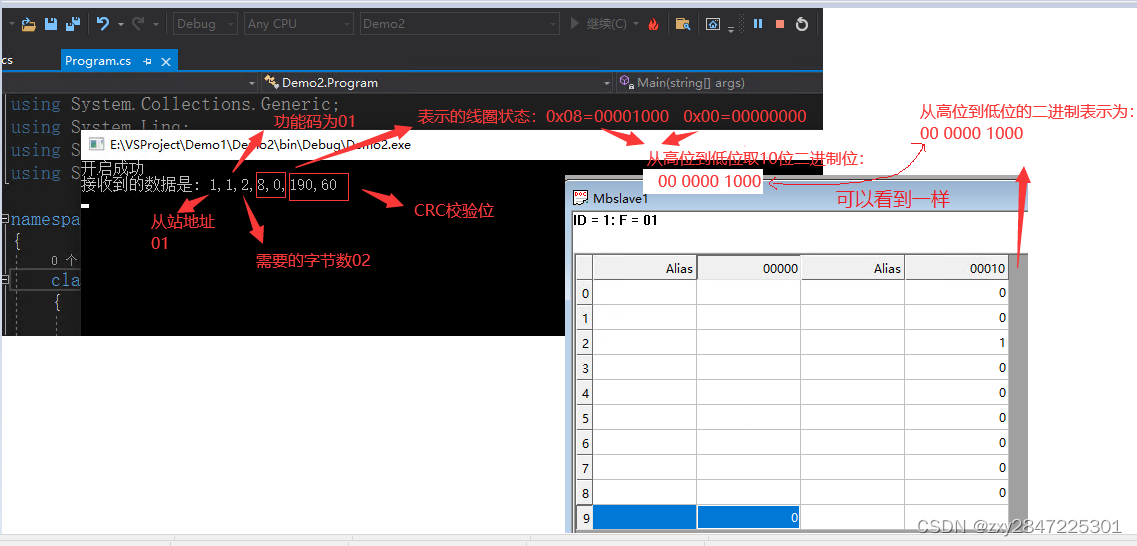
Modbus协议初探(C#实现)
由于作者水平有限,如有写得不对得地方请指正 趁着今天休息,就折腾一下Modbus协议,之前零零散散的看过几篇博客,听说搞上位机开发的要会这个协议,虽然我不是搞上位机开发的,但个人对这个比较感兴趣。按照我个…...

【华为OD机试2023】静态扫描 C++ Java Python
【华为OD机试2023】静态扫描 C++ Java Python 前言 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能最优),不能保证通过率。 Tips1:机试为ACM 模式 你的代码需要处理输入输出,input/cin接收输入、…...
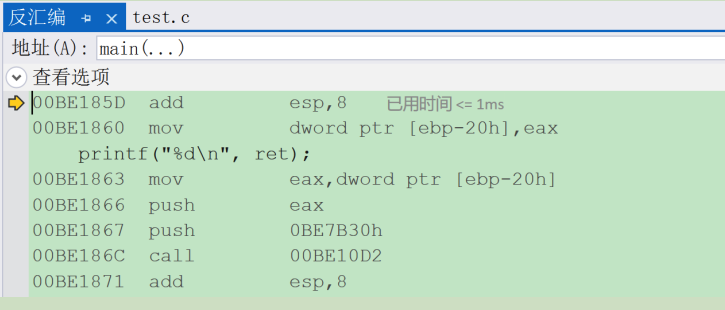
函数栈帧的创建和销毁(详解)
函数栈帧的创建和销毁🦖函数栈帧是什么?🦖函数栈帧的创建和销毁解析🐋栈是什么?🐋认识相关寄存器和汇编指令🐋解析函数栈帧的创建和销毁🐳预备知识🐳函数的调用堆栈&…...

【100个 Unity实用技能】 | 脚本无需挂载到游戏对象上也可执行的方法
Unity 小科普 老规矩,先介绍一下 Unity 的科普小知识: Unity是 实时3D互动内容创作和运营平台 。包括游戏开发、美术、建筑、汽车设计、影视在内的所有创作者,借助 Unity 将创意变成现实。Unity 平台提供一整套完善的软件解决方案ÿ…...

条件期望5
条件期望例题 随机图 从节点1开始, N为一个随机变量, 表示整个过程第一次出现"贪吃蛇"情形时, 所进行的步数.即Nk⇒Xk(1)∈{1,X(1),X2(1),...Xk−1(1)}其中1,X(1),X2(1),...Xk−1(1)各不相同N k \Rightarrow X^k(1) \in \{1,X(1), X^2(1),...X^{k-1}(1)\} \\ 其中1…...
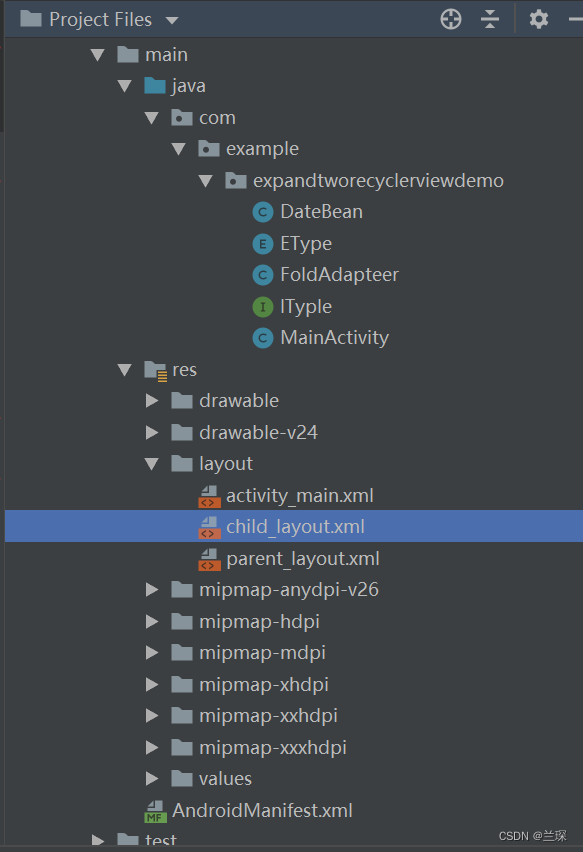
RecyclerView ViewType二级
实现效果描述: 1、点击recyclerview中item,列表下方出现其他样式的item,作为子item,如下所示 所需要的java文件和xml文件有: 1、创建FoldAdapteradapter, 在FoldAdapter中,定义两种不同的类型ÿ…...

将对象或数组存在 dom元素的属性上,最后取不到完整数据,只取到 [{
目录 一、问题 二、问题及解决方法 三、总结 一、问题 1.我需要在dom元素里面添加了一个属性test存一个对象数组temp,以便我下一次找到这个dom元素时可以直接拿到属性里面的数据来渲染页面。 2.dom 属性上存 对象和数组,必须先JSON.stringify(arr),转…...
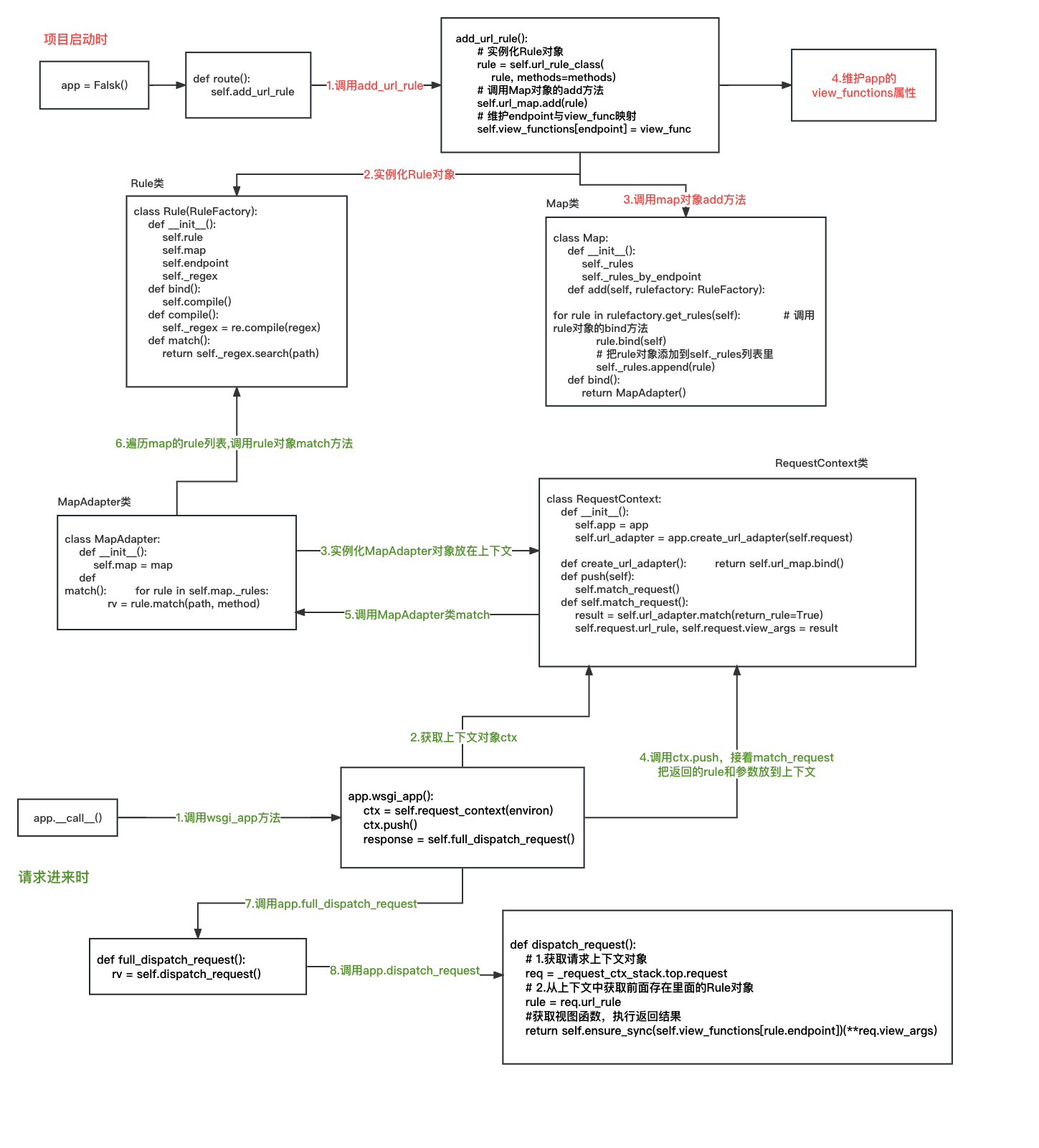
Flask源码篇:Flask路由规则与请求匹配过程(超详细,易懂)
目录1 启动时路由相关操作(1)分析app.route()(2)分析add_url_rule()(3)分析Rule类(4)分析Map类(5)分析MapAdapter类(6)分析 url_rule_…...

Jmeter接口测试教程之【参数化技巧总结】,总有一个是你不知道的
目录:导读 一、随机值 二、随机字符串 三、时间戳 四、唯一字符串UUID 说起接口测试,相信大家在工作中用的最多的还是Jmeter。 大家看这个目录就知道jmeter的应用有多广泛了:https://www.bilibili.com/video/BV1e44y1X78S/? JMeter是一个…...

缓存与数据库的双写一致性
背景 在高并发的业务场景下,系统的性能瓶颈往往是出现在数据库上,用户并发访问过大,压力都打到数据库上。所以一般都会用redis做缓存层,起到一个缓冲作用,让请求先访问到缓存层,而不是直接去访问数据库&am…...
)
力扣-213打家劫舍II(dp)
力扣-213打家劫舍II 1、题目 213. 打家劫舍 II 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通…...
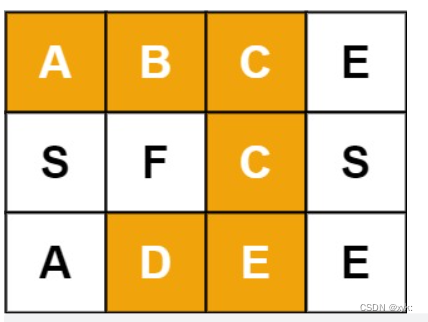
关于【网格结构】岛屿类问题的通用解法DFS(深度遍历)遍历框架+回溯+剪枝总结
最近在刷力扣时遇见的问题,自己总结加上看了力扣大佬的知识总结写下本篇文章,我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题…...

【LeetCode】982. 按位与为零的三元组
982. 按位与为零的三元组 题目描述 给你一个整数数组 nums ,返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件: 0 < i < nums.length0 < j < nums.length0 < k < num…...

Linux内核源码进程原理分析
Linux内核源码进程原理分析一、Linux 内核架构图二、进程基础知识三、Linux 进程四要素四、task_struct 数据结构主要成员五、创建新进程分析六、剖析进程状态迁移七、写时复制技术一、Linux 内核架构图 二、进程基础知识 Linux 内核把进程称为任务(task),进程的虚…...

电子技术——CMOS反相器
电子技术——CMOS反相器 在本节,我们深入学习CMOS反相器。 电路原理 下图是我们要研究的CMOS反相器的原理图: 下图展示了当输入 vIVDDv_I V_{DD}vIVDD 时的 iD−vDSi_D-v_{DS}iD−vDS 曲线: 我们把 QNQ_NQN 当做是驱动源&#x…...
)
gazebo仿真轨迹规划+跟踪(不在move_base框架下)
以Tianbot为例子,开源代码如下: https://github.com/tianbot/tianbot_mini GitHub - tianbot/abc_swarm: Ant Bee Cooperative Swarm, indicating air-ground cooperation. This repository is for Tianbot Mini and RoboMaster TT swarm kit. 1.在…...

C. Good Subarrays(前缀和)
C. Good Subarrays一、问题二、分析三、代码一、问题 二、分析 这道题目的意思就是给我们一个数组,然后我们从数组中选取一个连续的区间,这个区间满足条件:区间内的元素和等于区间的长度。 对于区间和问题我们先想到的是前缀和的算法。 那…...
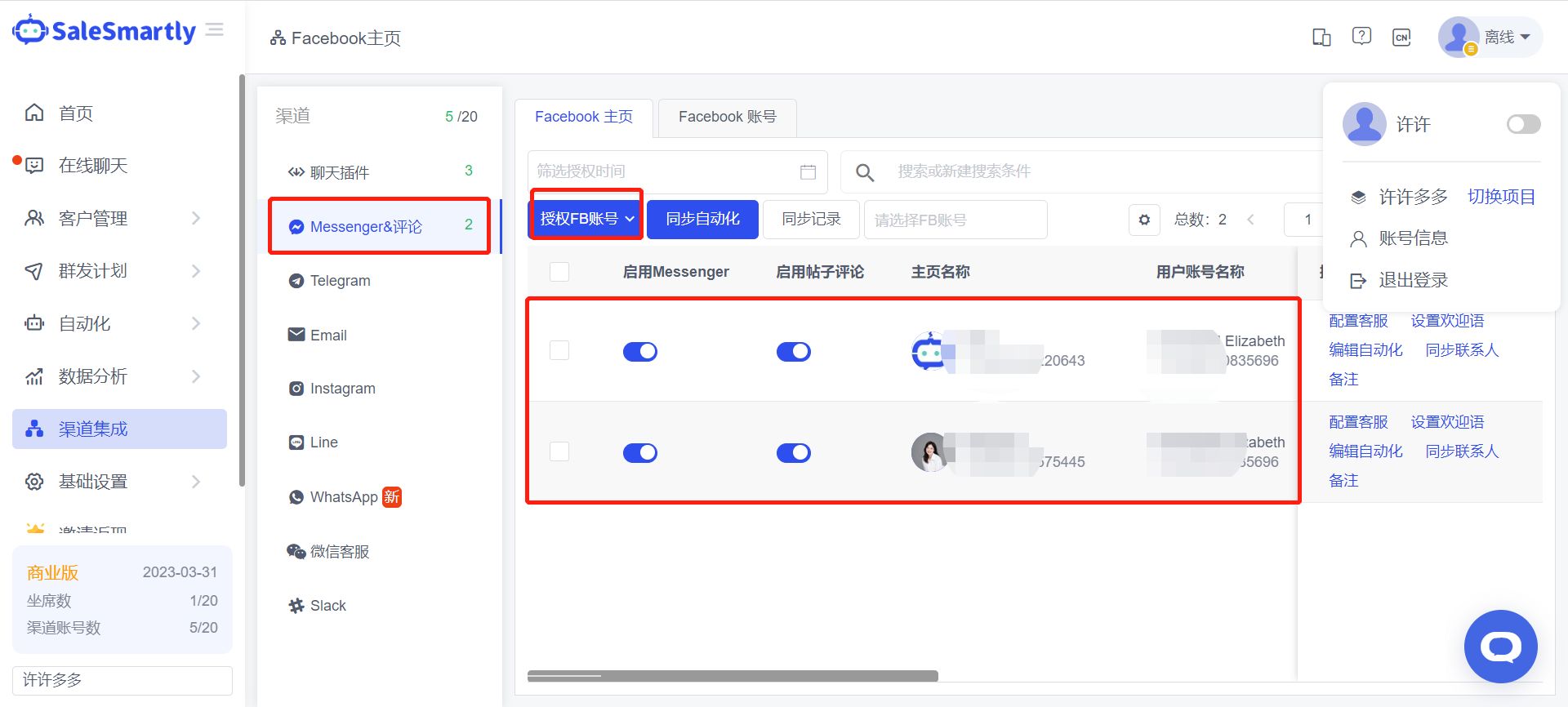
关于Facebook Messenger CRM,这里有你想要知道的一切
关于Facebook Messenger CRM,这里有你想要知道的一切!想把Facebook Messenger与你的CRM整合起来吗?这篇博文是为你准备的! 我们将介绍有关获得Facebook Messenger CRM整合的一切信息。然后,我们将解释为什么你需要像SaleSmartly&a…...
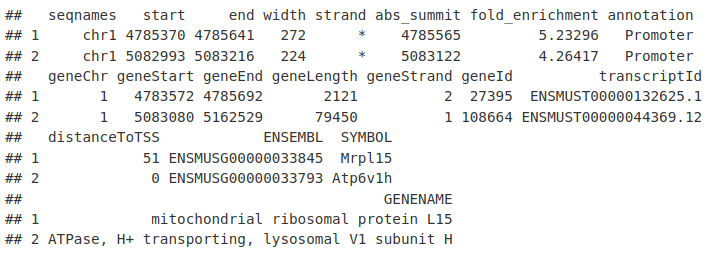
ChIP-seq 分析:数据与Peak 基因注释(10)
动动发财的小手,点个赞吧! 1. 数据 今天,我们将继续回顾我们在上一次中研究的 Myc ChIPseq。这包括用于 MEL 和 Ch12 细胞系的 Myc ChIPseq。 可在此处[1]找到 MEL 细胞系中 Myc ChIPseq 的信息和文件可在此处[2]找到 Ch12 细胞系中 Myc ChIP…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
