Potions (Hard Version) and (Easy Version)(背包DP + 反悔贪心)
@[TOC](Potions (Hard Version) and (Easy Version))
一、Potions(Easy Version)
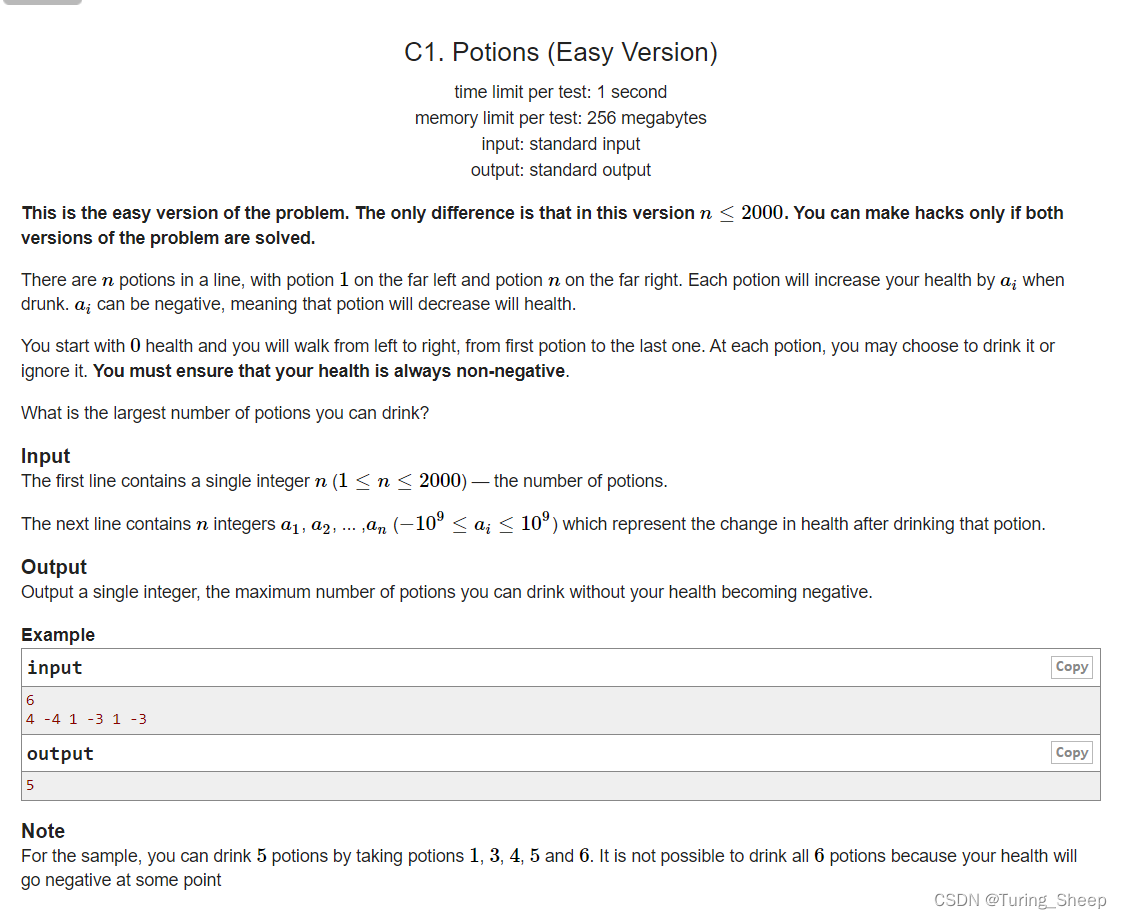
1、问题
2、分析(背包DP + 贪心)
简而言之就是我们需要从左到右开始选数字,选的过程中我们需要保证我们选的数字的和始终是大于等于0的,在满足这个条件的情况下求出我们所选的数字的个数的最大值。
由于这个简单版本的数据范围是2000,还是比较小的,所以我们可以使用O(n2)O(n^2)O(n2)的DP来解决。
假设我们的DP数组是: f[i][j]f[i][j]f[i][j]
这里的一个难点就是这个数组的含义是什么?
我们这里的定义是:在前iii个数字里面选,恰好选择jjj个数字时,数字之和的最大值。
我们先来解释一下,为什么我们要存储最大值。
假设我们在前iii个物品里选择了jjj个,那么这jjj个数字的和越大,我们后续的选择空间越大,这是一种贪心的想法。
那么我们如何求出最后的结果呢?
根据题目要求,我们的f[i][j]≥0f[i][j]\geq 0f[i][j]≥0。
所以我们可以去遍历f[n][i]f[n][i]f[n][i],只要这个数大于等于0,我们就可以让我们的ans=ians = ians=i。最后一个大于等于0的f[n][i]f[n][i]f[n][i]所对应的iii就是我们的答案。
转移方程:
f[i][j]={f[i−1][j]max(f[i−1][j−1]+a[i],f[i−1][j])f[i−1][j−1]≥0f[i][j] = \begin{cases} f[i - 1][j]\\ max\bigg(f[i - 1][j - 1] + a[i], f[i -1][j]\bigg)&f[i- 1][j- 1]\geq 0 \end{cases} f[i][j]=⎩⎨⎧f[i−1][j]max(f[i−1][j−1]+a[i],f[i−1][j])f[i−1][j−1]≥0
因为只有在当前数字的和大于等于0的时候,我们才能去选下一个。所以我们需要让f[i−1][j−1]f[i-1][j-1]f[i−1][j−1]大于0。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 2010;
ll a[N], f[N][N];
void solve()
{int n;cin >> n;for(int i = 1; i <= n; i ++ )cin >> a[i];memset(f, 0xcf, sizeof f);f[0][0] = 0;for(int i = 1; i <= n; i ++ ){for(int j = 0; j <= i; j ++ ){f[i][j] = f[i - 1][j];if(j >= 1 && f[i - 1][j - 1] >= 0)f[i][j] = max(f[i - 1][j - 1] + a[i], f[i][j]);}}int ans = 0;for(int i = 0; i <= n; i ++ ){if(f[n][i] >= 0)ans = i;}cout << ans << endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();
}
二、Potions(Hard Version)
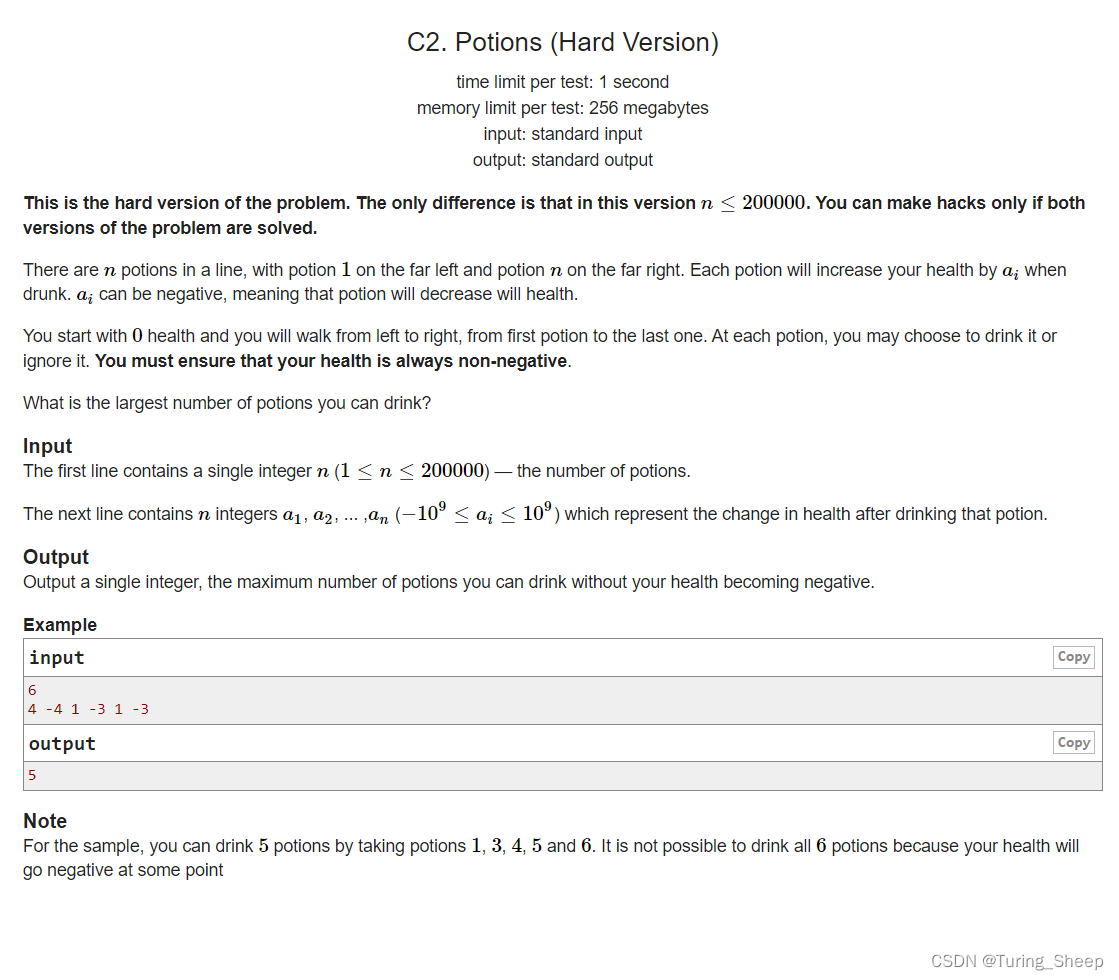
1、问题
2、分析(反悔贪心)
这道题和上一道题的唯一区别就是我们的数据范围变得很大,所以二维DP数组是存储不下的,即使我们逆序遍历从而优化掉一维的话,我们的时间复杂度也是平方级别的,依然过不了。
因此,我们就只能想别的方法了。
这里采用的也是贪心策略。
我们从左到右开始枚举每一个数,在枚举的过程中我们会发现,正数一定是要选择的,所以遇到正数我们就加上即可。
这里的重点是负数的选择。
从左到右枚举每一个数,假设每一个数都选择,当当前的总和小于0的时候,我们就把从开始位置到当前位置之间的负数中最小的一个删掉。
为什么这样做呢?
假设枚举到第iii个的时候,总和sumsumsum从正数变成负数。再假设此时我们选择了kkk个数(不算第iii个)。
那么很明确的是,sumsumsum是由于第iii个数的加入才变成了负数, 说明第iii个数一定是负数。那么我们当然可以选择删除第iii个数,这样的话,我们就能保证sumsumsum依然是正数。
但不选第iii个数就是最优解吗?其实不一定的。
如果在111到iii之间存在一个小于第iii个数的最小的负数。如果我们删除了这个最小的负数,选择了第iii个数,我们将这两个数字记作minminmin和ppp。那么此时的总和就是sum−min+psum-min+psum−min+p由minminmin小于ppp所以p−minp-minp−min是大于0的。
而此时我们选了几个数呢?选择第iii个数,我们此时总共选了k+1k+1k+1个数,删除最小的负数,即再减一,所以总共还是选择了kkk个数。
其实很容易证明,当我们经过上述操作后,我们的sumsumsum是从111到iii中选择kkk个数时,最大的数字和。式子sum+p−minvsum+p-minvsum+p−minv就可以证明,因为minvminvminv是最小的,所以这个式子是最大的。
也就是说,通过上述的操作,我们维护的都是选择kkk个数时的最优解(sumsumsum最大)。
通过刚才的easyeasyeasy版本的讲解,我们也知道,选择相同个数的数字时,总和越大越好,总和越大说明我们后续的选择越多。
不妨看出,通过上面的操作,我们的kkk是不受影响的, 即这样调整不会使得我们的答案变小。
如果感性认知的话,就是我们时刻保持最优解去看能不能喝下一瓶。
综上,我们的做法可以描述为,从左到右遍历,利用总和sumsumsum记录,只要sumsumsum小于0了,我们就删除遍历过的数中的最小负数。
在一堆数字中选出一个最值,我们可以使用优先队列。
我们的时间复杂度即O(nlogn)O(nlogn)O(nlogn)。
而我们发现,这个贪心过程中我们出现了反悔的操作,即我们一开始喝了一瓶,但是后来发现喝的这一瓶不是最优解,那么我们就反悔了,这一瓶不喝了。这种贪心就被称为反悔贪心。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 2e5 + 10;
ll a[N], f[N];
void solve()
{int n;cin >> n;for(int i = 0; i < n; i ++ )cin >> a[i];priority_queue<int>q;ll ans = 0, sum = 0;for(int i = 0; i < n; i ++ ){sum += a[i];ans ++;if(a[i] < 0)q.push( - a[i]);if(sum < 0){sum += q.top();q.pop();ans --;}}cout << ans << endl;}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();
}
相关文章:

Potions (Hard Version) and (Easy Version)(背包DP + 反悔贪心)
[TOC](Potions (Hard Version) and (Easy Version)) 一、Potions(Easy Version) 1、问题 2、分析(背包DP 贪心) 简而言之就是我们需要从左到右开始选数字,选的过程中我们需要保证我们选的数字的和始终是大于等于0的,在满足这个…...

剑指 Offer II 017. 含有所有字符的最短字符串
题目链接 剑指 Offer II 017. 含有所有字符的最短字符串 hard 题目描述 给定两个字符串 s和 t。返回 s中包含 t的所有字符的最短子字符串。如果 s中不存在符合条件的子字符串,则返回空字符串 ""。 如果 s中存在多个符合条件的子字符串,返回任…...
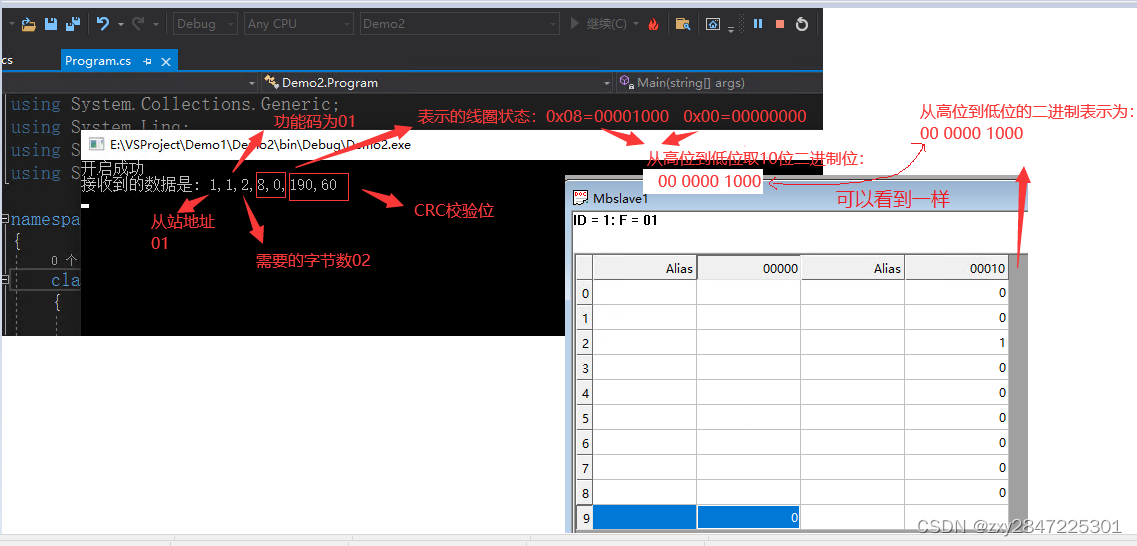
Modbus协议初探(C#实现)
由于作者水平有限,如有写得不对得地方请指正 趁着今天休息,就折腾一下Modbus协议,之前零零散散的看过几篇博客,听说搞上位机开发的要会这个协议,虽然我不是搞上位机开发的,但个人对这个比较感兴趣。按照我个…...

【华为OD机试2023】静态扫描 C++ Java Python
【华为OD机试2023】静态扫描 C++ Java Python 前言 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能最优),不能保证通过率。 Tips1:机试为ACM 模式 你的代码需要处理输入输出,input/cin接收输入、…...
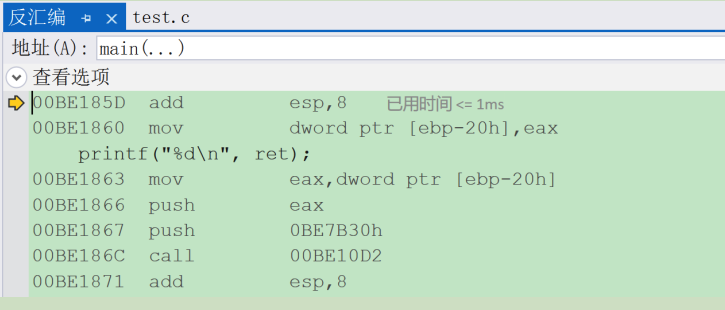
函数栈帧的创建和销毁(详解)
函数栈帧的创建和销毁🦖函数栈帧是什么?🦖函数栈帧的创建和销毁解析🐋栈是什么?🐋认识相关寄存器和汇编指令🐋解析函数栈帧的创建和销毁🐳预备知识🐳函数的调用堆栈&…...

【100个 Unity实用技能】 | 脚本无需挂载到游戏对象上也可执行的方法
Unity 小科普 老规矩,先介绍一下 Unity 的科普小知识: Unity是 实时3D互动内容创作和运营平台 。包括游戏开发、美术、建筑、汽车设计、影视在内的所有创作者,借助 Unity 将创意变成现实。Unity 平台提供一整套完善的软件解决方案ÿ…...

条件期望5
条件期望例题 随机图 从节点1开始, N为一个随机变量, 表示整个过程第一次出现"贪吃蛇"情形时, 所进行的步数.即Nk⇒Xk(1)∈{1,X(1),X2(1),...Xk−1(1)}其中1,X(1),X2(1),...Xk−1(1)各不相同N k \Rightarrow X^k(1) \in \{1,X(1), X^2(1),...X^{k-1}(1)\} \\ 其中1…...
RecyclerView ViewType二级
实现效果描述: 1、点击recyclerview中item,列表下方出现其他样式的item,作为子item,如下所示 所需要的java文件和xml文件有: 1、创建FoldAdapteradapter, 在FoldAdapter中,定义两种不同的类型ÿ…...

将对象或数组存在 dom元素的属性上,最后取不到完整数据,只取到 [{
目录 一、问题 二、问题及解决方法 三、总结 一、问题 1.我需要在dom元素里面添加了一个属性test存一个对象数组temp,以便我下一次找到这个dom元素时可以直接拿到属性里面的数据来渲染页面。 2.dom 属性上存 对象和数组,必须先JSON.stringify(arr),转…...
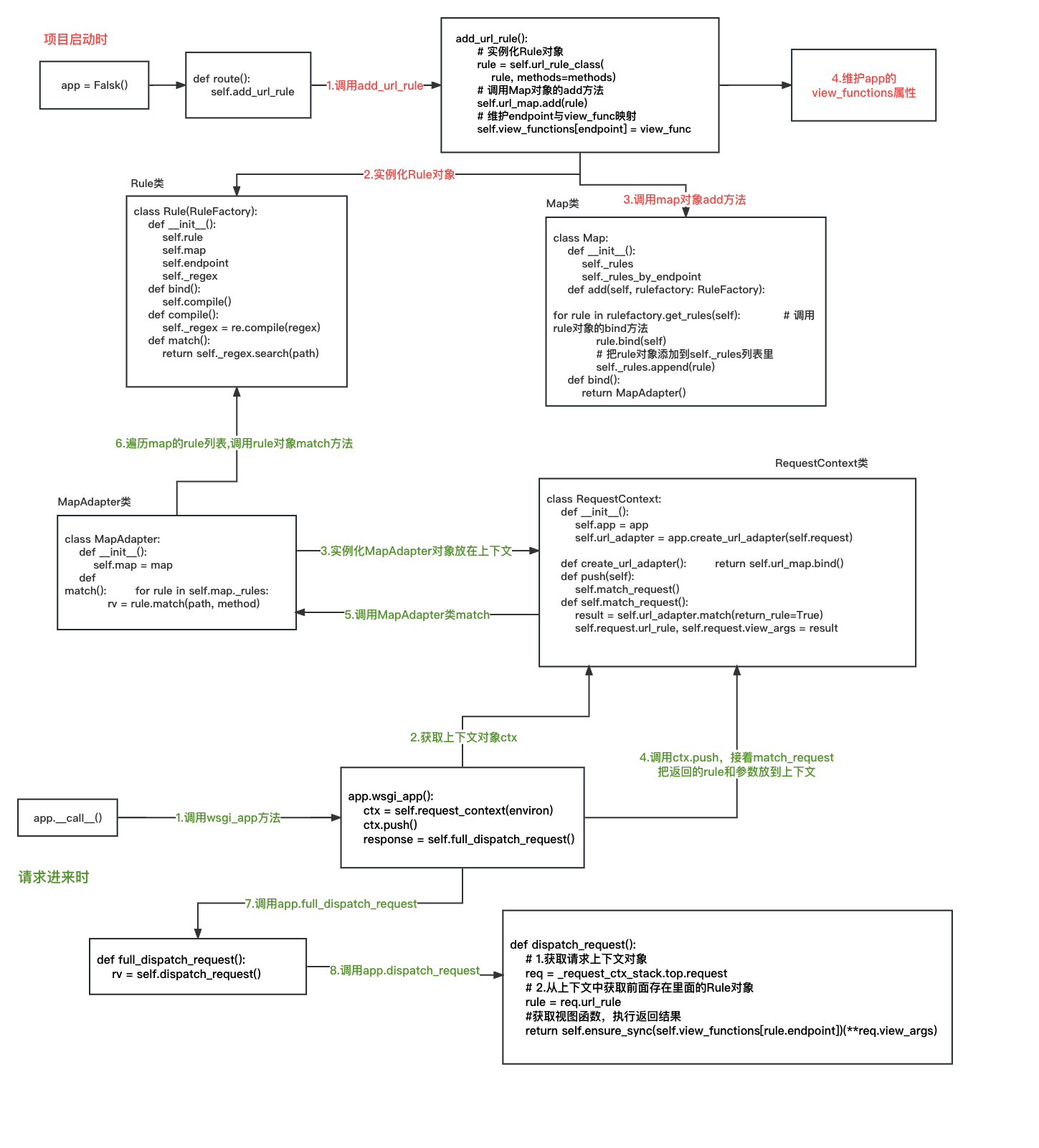
Flask源码篇:Flask路由规则与请求匹配过程(超详细,易懂)
目录1 启动时路由相关操作(1)分析app.route()(2)分析add_url_rule()(3)分析Rule类(4)分析Map类(5)分析MapAdapter类(6)分析 url_rule_…...

Jmeter接口测试教程之【参数化技巧总结】,总有一个是你不知道的
目录:导读 一、随机值 二、随机字符串 三、时间戳 四、唯一字符串UUID 说起接口测试,相信大家在工作中用的最多的还是Jmeter。 大家看这个目录就知道jmeter的应用有多广泛了:https://www.bilibili.com/video/BV1e44y1X78S/? JMeter是一个…...

缓存与数据库的双写一致性
背景 在高并发的业务场景下,系统的性能瓶颈往往是出现在数据库上,用户并发访问过大,压力都打到数据库上。所以一般都会用redis做缓存层,起到一个缓冲作用,让请求先访问到缓存层,而不是直接去访问数据库&am…...
)
力扣-213打家劫舍II(dp)
力扣-213打家劫舍II 1、题目 213. 打家劫舍 II 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通…...
关于【网格结构】岛屿类问题的通用解法DFS(深度遍历)遍历框架+回溯+剪枝总结
最近在刷力扣时遇见的问题,自己总结加上看了力扣大佬的知识总结写下本篇文章,我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题…...

【LeetCode】982. 按位与为零的三元组
982. 按位与为零的三元组 题目描述 给你一个整数数组 nums ,返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件: 0 < i < nums.length0 < j < nums.length0 < k < num…...

Linux内核源码进程原理分析
Linux内核源码进程原理分析一、Linux 内核架构图二、进程基础知识三、Linux 进程四要素四、task_struct 数据结构主要成员五、创建新进程分析六、剖析进程状态迁移七、写时复制技术一、Linux 内核架构图 二、进程基础知识 Linux 内核把进程称为任务(task),进程的虚…...

电子技术——CMOS反相器
电子技术——CMOS反相器 在本节,我们深入学习CMOS反相器。 电路原理 下图是我们要研究的CMOS反相器的原理图: 下图展示了当输入 vIVDDv_I V_{DD}vIVDD 时的 iD−vDSi_D-v_{DS}iD−vDS 曲线: 我们把 QNQ_NQN 当做是驱动源&#x…...
)
gazebo仿真轨迹规划+跟踪(不在move_base框架下)
以Tianbot为例子,开源代码如下: https://github.com/tianbot/tianbot_mini GitHub - tianbot/abc_swarm: Ant Bee Cooperative Swarm, indicating air-ground cooperation. This repository is for Tianbot Mini and RoboMaster TT swarm kit. 1.在…...

C. Good Subarrays(前缀和)
C. Good Subarrays一、问题二、分析三、代码一、问题 二、分析 这道题目的意思就是给我们一个数组,然后我们从数组中选取一个连续的区间,这个区间满足条件:区间内的元素和等于区间的长度。 对于区间和问题我们先想到的是前缀和的算法。 那…...
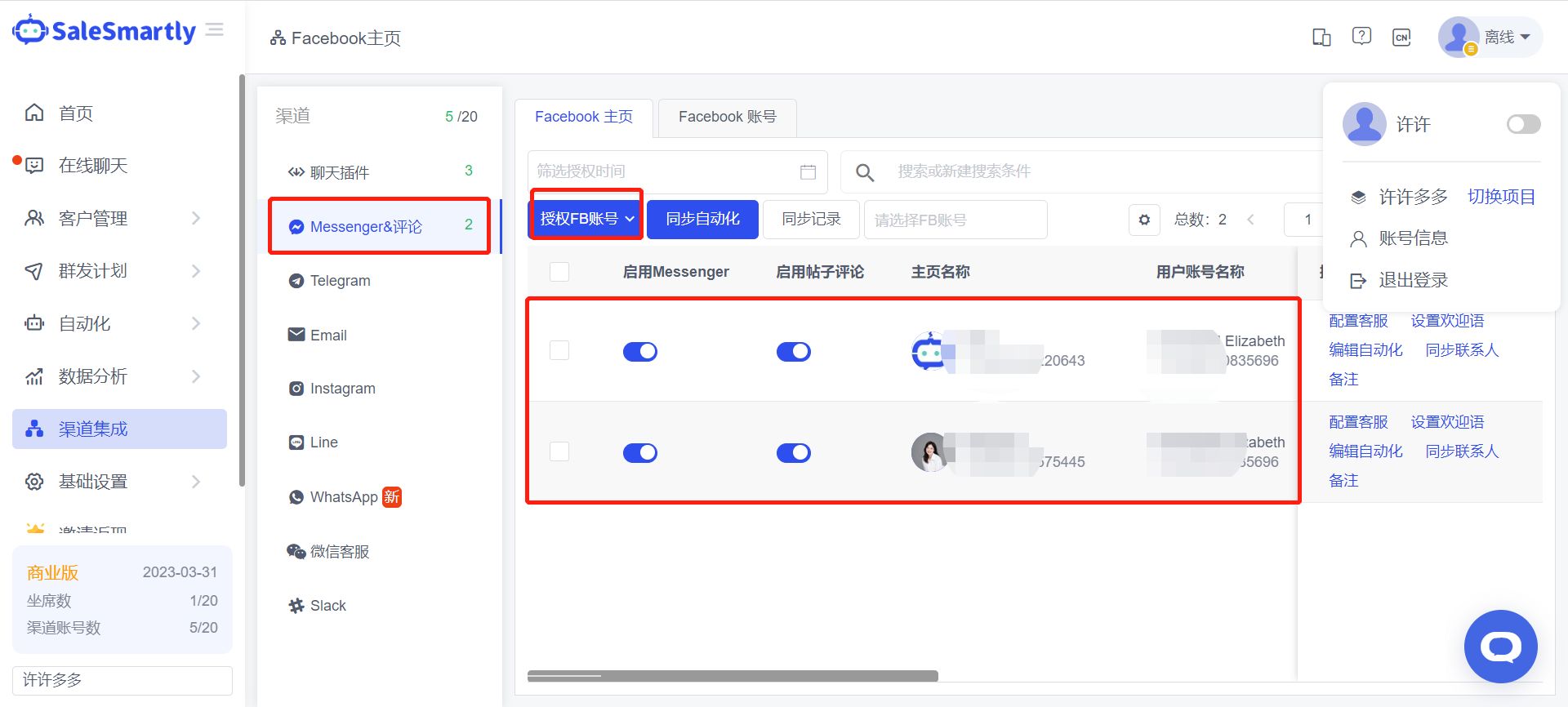
关于Facebook Messenger CRM,这里有你想要知道的一切
关于Facebook Messenger CRM,这里有你想要知道的一切!想把Facebook Messenger与你的CRM整合起来吗?这篇博文是为你准备的! 我们将介绍有关获得Facebook Messenger CRM整合的一切信息。然后,我们将解释为什么你需要像SaleSmartly&a…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
