「数据结构」栈和队列
栈
栈的基本概念
- 定义
- 栈是只允许在一端进行插入或删除操作的线性表
- 栈顶:线性表允许进行插入删除的那一端
- 栈底:固定的,不允许进行插入和删除的另一端
- 空栈:不含任何元素
- 特点:后进先出(LIFO)
- 基本操作
InitStack(&S):初始化一个空栈SStackEmpty(S):判断一个栈是否为空,若栈S为空则返回true,否则返回falsePush(&S,x):进栈,若栈S未满,则将x加入使之成为新栈顶Pop(&S,%=&x):出栈,若栈S非空,则用x返回栈顶元素GetTop(S,&x):读栈顶元素,若栈S非空,则用x返回栈顶元素DestroyStack(&S):销毁栈,并释放栈S占用的存储空间
- 卡特兰数:n个不同元素进栈,出栈元素的不同排列的个数为 1 n + 1 C 2 n n \frac{1}{n+1}C^n_{2n} n+11C2nn
栈的顺序存储结构
- 顺序栈的定义
#define MaxSize 10 //定义栈中元素的最大个数typedef struct{ElemType data[MaxSize]; //静态数组存放栈中元素int top; //栈顶元素
}SqStack;void testStack(){SqStack S; //声明一个顺序栈(分配空间)//连续的存储空间大小为 MaxSize*sizeof(ElemType)
}
- 基本操作
#define MaxSize 10 //定义栈中元素的最大个数typedef struct{ElemType data[MaxSize]; //静态数组存放栈中元素int top; //栈顶元素
}SqStack;//初始化栈
void InitStack(SqStack &S){S.top = -1; //初始化栈顶指针
}//判栈空
bool StackEmpty(SqStack S){if(S.top == -1) //栈空return true;else //栈不空return false;
}//新元素进栈
bool Push(SqStack &S, ElemType x){if(S.top == MaxSize - 1) //栈满return false;S.top = S.top + 1; //指针先加1S.data[S.top] = x; //新元素入栈/*S.data[++S.top] = x;*/return true;
}//出栈
bool Pop(SqStack &x, ElemType &x){if(S.top == -1) //栈空return false;x = S.data[S.top]; //先出栈S.top = S.top - 1; //栈顶指针减1return true;/*x = S.data[S.top--];*///只是逻辑上的删除,数据依然残留在内存里
}//读栈顶元素
bool GetTop(SqStack S, ElemType &x){if(S.top == -1)return false;x = S.data[S.top]; //x记录栈顶元素return true;
}void testStack(){SqStack S; //声明一个顺序栈(分配空间)InitStack(S);//...
}
- 栈满条件:
top==MaxSize - 顺序栈的缺点:栈的大小不可变
- 共享栈
- 定义:利用栈底位置相对不变的特性,可以让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间的中间延伸
栈的链式存储结构
与链表类似,入栈和出栈的操作都在链表的表头进行
队列
队列的概念
- 定义:队列是只允许在一端进行插入(入队),在另一端删除(出队)的线性表
- 队头:允许删除的一端
- 队尾:允许插入的一端
- 空队列:不含任何元素的空表
- 队列的特点:先进先出(FIFO)
- 队列的基本操作
InitQueue(&Q): 初始化队列,构造一个空队列QDestroyQueue(&Q): 销毁队列,并释放队列Q所占用的内存空间EnQueue(&Q, x): 入队,若队列Q未满,将x加入,使之成为新的队尾DeQueue(&Q, &x): 出队,若队列Q非空,删除队头元素,并用x返回GetHead(Q,&x): 读队头元素,若队列Q非空,则将队头元素赋值给xQueueEmpty(Q): 判队列空,若队列Q为空,则返回true,否则返回false
队列的顺序存储结构
- 队列的顺序实现
# define MaxSize 10; //定义队列中元素的最大个数
typedef struct{ElemType data[MaxSize]; //用静态数组存放队列元素int front, rear; //队头指针和队尾指针
}SqQueue;
- 初始化操作
//初始化队列
void InitQueue(SqQueue &Q){//初始化时,队头、队尾指针指向0Q.rear = Q.front = 0;
}// 判断队列是否为空
bool QueueEmpty(SqQueue 0){if(Q.rear == Q.front) //队空条件return true;else return false;
}
- 入队操作
bool EnQueue(SqQueue &Q, ElemType x){if((Q.rear+1)%MaxSize == Q.front) //队满return false; //队满报错Q.data[Q.rear] = x; //将x插入队尾Q.rear = (Q.rear + 1) % MaxSize; //队尾指针加1取模return true;
}
- 出队操作
//出队,删除一个队头元素,用x返回
bool DeQueue(SqQueue &Q, ElemType &x){if(Q.rear == Q.front) //队空报错return false; x = Q.data[Q.front];Q.front = (Q.front + 1) % MaxSize; //队头指针后移动return true;
}
- 获得队头元素
bool GetHead(SqQueue &Q, ElemType &x){if(Q.rear == Q.front) //队空报错return false; x = Q.data[Q.front];return true;
}
- 判断队列已满/已空
- 方案一:牺牲一个存储单元(实现代码同1)
- 初始化时:
rear=front=0; - 队空条件:
Q.rear==Q.front; - 队满条件:
(Q.rear+1)%MaxSize == Q.front - 队列元素个数:
(rear+MaxSize-front)%MaxSize;
- 初始化时:
- 方案二
- 实现
#define MaxSize 10; //定义队列中元素的最大个数 typedef struct{ElemType data[MaxSize]; //用静态数组存放队列元素int front, rear; //队头指针和队尾指针int size; }SqQueue;- 初始化时
rear=front=0; size=0;- 插入成功:
size++; - 删除成功:
size--; - 队满条件:
size==Maxsize; - 队空条件:
size==0;
- 方案三
- 实现
#define MaxSize 10; //定义队列中元素的最大个数 typedef struct{ElemType data[MaxSize]; //用静态数组存放队列元素int front, rear; //队头指针和队尾指针int tag; //最近进行的是删除/插入 }SqQueue;- 初始化时
rear=front=0; tag=0;- 插入成功:
tag=1; - 删除成功:
tag=0; - 队满条件:
rear==front&&tag==1; - 队空条件:
rear==front&&tag==0;
- 方案一:牺牲一个存储单元(实现代码同1)
队列的链式存储结构
- 定义队列
typedef struct LinkNode{ //链式队列结点ElemType data;struct LinkNode *next;
}typedef struct{ //链式队列LinkNode *front, *rear; //队列的队头和队尾指针
}LinkQueue;
-
初始化
- 带头结点
void InitQueue(LinkQueue &Q){//初始化时,front、rear都指向头结点Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));Q.front -> next = NULL; }//判断队列是否为空 bool IsEmpty(LinkQueue Q){if(Q.front == Q.rear) //也可用 Q.front -> next == NULLreturn true;elsereturn false; }- 不带头结点
void InitQueue(LinkQueue &Q){//初始化时,front、rear都指向NULLQ.front = NULL;Q.rear = NULL; }//判断队列是否为空 bool IsEmpty(LinkQueue Q){if(Q.front == NULL)return true;elsereturn false; } -
入队
- 带头结点
//新元素入队 (表尾进行) void EnQueue(LinkQueue &Q, ElemType x){LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode)); //申请一个新结点s->data = x;s->next = NULL; //s作为最后一个结点,指针域指向NULLQ.rear->next = s; //新结点插入到当前的rear之后Q.rear = s; //表尾指针指向新的表尾 }- 不带头结点
//新元素入队 void EnQueue(LinkQueue &Q, ElemType x){LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode)); //申请一个新结点s->data = x;s->next = NULL;if(Q.front==NULL){ //在空队列中插入第一个元素Q.front=s; //修改队头队尾指针Q.rear=s;}else{Q.rear->next=s; //新结点插入到rear结点之后Q.rear=s; //修改rear指针} } -
出队
- 带头结点
//队头元素出队 bool DeQueue(LinkQueue &Q, ElemType &x){if(Q.front == Q.rear)return false; //空队LinkNode *p = Q.front->next; //p指针指向即将删除的结点x = p->data;Q.front->next = p->next; //修改头结点的next指针if(Q.rear == p) //此次是最后一个结点出队Q.rear = Q.front; //修改rear指针free(p); //释放结点空间return true; }- 不带头结点
//队头元素出队 bool DeQueue(LinkQueue &Q, ElemType &x){if(Q.front == Q.rear)return false; //空队LinkNode *p = Q.front; //p指针指向即将删除的结点x = p->data;Q.front = p->next; //修改头结点的next指针if(Q.rear == p){ //此次是最后一个结点出队Q.rear==NULL:Q.front==NULL;} free(p); //释放结点空间return true; }
双端队列
- 定义:只允许从两端插入、两端删除的线性表
- 输入受限的双端队列:允许一端插入,两端删除的线性表
- 输出受限的双端队列:允许两端插入,一端删除的线性表
栈和队列的应用
栈在括号匹配中的应用
#define MaxSize 10 typedef struct{char data[MaxSize];int top;
} SqStack;//初始化栈
InitStack(SqStack &S)//判断栈是否为空
bool StackEmpty(SqStack &S)//新元素入栈
bool Push(SqStack &S, char x)//栈顶元素出栈,用x返回
bool Pop(SqStack &S, char &x)bool bracketCheck(char str[], int length){SqStack S; //声明InitStack(S); //初始化栈for(int i=0; i<length; i++){if(str[i] == '(' || str[i] == '[' || str[i] == '{'){Push(S, str[i]); //扫描到左括号,入栈}else{if(StackEmpty(S)) //扫描到右括号,且当前栈空return false; //匹配失败char topElem; //存储栈顶元素Pop(S, topElem); //栈顶元素出栈if(str[i] == ')' && topElem != '(' )return false;if(str[i] == ']' && topElem != '[' )return false;if(str[i] == '}' && topElem != '{' )return false; }}StackEmpty(S); //栈空说明匹配成功
}
栈在表达式值中的应用
中缀表达式
(需要界限符)
- 规则:运算符在两个操作数中间
- 例
- a + b
- a + b - c
- a + b - c*d
后缀表达式 (逆波兰表达式)
- 规则:运算符在两个操作数后面
- 例
- a b +
- ab+ c - / a bc- +
- ab+ cd* -
- 中缀表达式转后缀表达式
- 确定中缀表达式中各个运算符的运算顺序
- 选择下一个运算符,按照[左操作数 右操作数 运算符]的方式组合成一个新的操作数
- 如果还有运算符没被处理,继续步骤2
“左优先”原则: 只要左边的运算符能先计算,就优先算左边的 (保证运算顺序唯一)
- 用栈实现中缀表达式转后缀表达式
- 初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况
- 遇到操作数: 直接加入后缀表达式
- 遇到界限符: 遇到 ‘(’ 直接入栈; 遇到 ‘)’ 则依次弹出栈内运算符并加入后缀表达式,直到弹出 ‘(’ 为止。注意: ‘(’ 不加入后缀表达式
- 遇到运算符: 依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到 ‘(’ 或栈空则停止。之后再把当前运算符入栈
- 按上述方法处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式
- 初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况
- 后缀表达式的计算:从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应的运算,合体为一个操作数
- 用栈实现后缀表达式的计算(栈用来存放当前暂时不能确定运算次序的操作数)
- 从左往后扫描下一个元素,直到处理完所有元素
- 若扫描到操作数,则压入栈,并回到步骤1;否则执行步骤3
- 若扫描到运算符,则弹出两个栈顶元素,执行相应的运算,运算结果压回栈顶,回到步骤1
先出栈的是“右操作数”
前缀表达式 (波兰表达式)
- 规则:运算符在两个操作数前面
- 例
-
- a b
- +ab c
-
- +ab *cd
-
- 中缀表达式转前缀表达式
- 确定中缀表达式中各个运算符的运算顺序
- 选择下一个运算符,按照[运算符 左操作数 右操作数]的方式组合成一个新的操作数
- 如果还有运算符没被处理,就继续执行步骤2
“右优先”原则: 只要右边的运算符能先计算,就优先算右边的;
- 用栈实现前缀表达式的计算
- 从右往左扫描下一个元素,直到处理完所有元素
- 若扫描到操作数则压入栈,并回到步骤1,否则执行步骤3
- 若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到步骤1;
先出栈的是“左操作数”
4.中缀表达式的计算(用栈实现):两个算法的结合: 中缀转后缀 + 后缀表达式的求值
1. 初始化两个栈,操作数栈和运算符栈
2. 若扫描到操作数,压入操作数栈
3. 若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈 (期间也会弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈项元素并执行相应运算,运算结果再压回操作数栈)
栈在递归中的应用
- 函数调用的特点:最后被调用的函数最先执行结束(LIFO)
- 函数调用时,需要用一个栈存储
- 调用返回地址
- 实参
- 局部变量
- 递归调用时,函数调用栈称为 “递归工作栈”
- 每进入一层递归,就将递归调用所需信息压入栈顶
- 每退出一层递归,就从栈顶弹出相应信息
- 缺点: 太多层递归可能回导致栈溢出
数组和特殊矩阵
数组的定义
数组是由n(n>=1)个相同类型的数据元素构成的有限序列,每个数据元素称为一个数组元素,每个元素在n个线性关系中的序号称为该元素的下标,下标的取值范围称为数组的维界
数组的存储结构
- 一维数组
- 各数组元素大小相同,物理上连续存放
- 数组下标:默认从0开始
- 数组元素 a[i] 的存放地址 = L O C + i ∗ s i z e o f ( E l e m T y p e ) LOC + i * sizeof(ElemType) LOC+i∗sizeof(ElemType)
- LOC为数组起始地址
- 二维数组
- 行优先/列优先存储优点:实现随机存储
- M行N列的二维数组 b[M][N] 中,b[i][j]的存储地址:
- 行优先存储: L O C + ( i × N + j ) × s i z e o f ( E l e m T y p e ) LOC + (i×N + j) × sizeof(ElemType) LOC+(i×N+j)×sizeof(ElemType)
- 列优先存储: L O C + ( j × M + i ) × s i z e o f ( E l e m T y p e ) LOC + (j×M + i) × sizeof(ElemType) LOC+(j×M+i)×sizeof(ElemType)
- 普通矩阵的存储:使用二维数组存储
描述矩阵元素时,行、列号通常从1开始
描述数组时,通常下标从 0 开始
特殊矩阵的压缩存储
矩阵的压缩存储:为多个相同的非零元素只分配一个存储空间;对零元素不分配空间。
- 对称矩阵
- 若n 阶方阵中任意一个元素 a i , j a_{i,j} ai,j都有 a i , j = a j , i a_{i,j}=a_{j,i} ai,j=aj,i则该矩阵为对称矩阵
- 策略:只存储主对角线+下三角区;按行优先原则将各元素存入一维数组中
- 数组大小: n ( n + 1 ) 2 \frac{n(n+1)}{2} 2n(n+1)
- 元素下标对应关系:k为 a i , j a_{i,j} ai,j在一维数组中的下标
k = { i ( i − 1 ) 2 + j − 1 , i ≥ j ( 下三角区和主对角线元素 ) j ( j − 1 ) 2 + i − 1 , i < j ( 上三角区元素 a i , j = a j , i ) k= \left\{ \begin{array}{l} \frac{i(i-1)}{2}+j-1, \quad i \ge j \quad (下三角区和主对角线元素) \\ \frac{j(j-1)}{2}+i-1, \quad i<j \quad (上三角区元素a_{i,j}=a_{j,i}) \ \end{array} \right. k={2i(i−1)+j−1,i≥j(下三角区和主对角线元素)2j(j−1)+i−1,i<j(上三角区元素ai,j=aj,i)
- 三角矩阵
- 以主对角线划分,三角矩阵有上(下)三角两种。上(下)三角矩阵的下(上)三角(不含主对角线)中的元素均为常数。在大多数情况下,三角矩阵常数为零
- 策略:按行优先原则将元素存入一维数组中(同对称矩阵)。并在最后一个位置存储常量
- 元素下标对应关系:k为 a i , j a_{i,j} ai,j在一维数组中的下标
k = { i ( i − 1 ) 2 + j − 1 , i ≥ j ( 下三角区和主对角线元素 ) n ( n + 1 ) 2 , i < j ( 上三角区元素 a i , j = a j , i ) k= \left\{ \begin{array}{l} \frac{i(i-1)}{2}+j-1, \quad i \ge j \quad (下三角区和主对角线元素) \\ \frac{n(n+1)}{2}, \quad i<j \quad (上三角区元素a_{i,j}=a_{j,i}) \ \end{array} \right. k={2i(i−1)+j−1,i≥j(下三角区和主对角线元素)2n(n+1),i<j(上三角区元素ai,j=aj,i)
3. 三对角矩阵(带状矩阵)
1. 当 ∣ i − j ∣ > 1 |i-j|>1 ∣i−j∣>1时,有 a i , j = 0 ( 1 ≤ i , j ≤ n ) a_{i,j}=0 (1 \leq i,j \leq n) ai,j=0(1≤i,j≤n)
2. 策略:按行优先(或列优先) 原则,只存储带状部分
3. 元素下标对应关系:k为 a i , j a_{i,j} ai,j在一维数组中的下标 k=2i+j-3
稀疏矩阵
- 非零元系远远少于矩阵元素的个数
- 策略
- 顺序存储——三元组<行,列,值>
- 会失去随机存取的特性
- 十字链表法
- 顺序存储——三元组<行,列,值>
相关文章:

「数据结构」栈和队列
栈 栈的基本概念 定义 栈是只允许在一端进行插入或删除操作的线性表栈顶:线性表允许进行插入删除的那一端栈底:固定的,不允许进行插入和删除的另一端空栈:不含任何元素特点:后进先出(LIFO) 基…...

【机器学习笔记】5 机器学习实践
数据集划分 子集划分 训练集(Training Set):帮助我们训练模型,简单的说就是通过训练集的数据让我们确定拟合曲线的参数。 验证集(Validation Set):也叫做开发集( Dev Set …...

C++ //练习 7.5 在你的Person类中提供一些操作使其能够返回姓名和住址。这些函数是否应该是const的呢?解释原因。
C Primer(第5版) 练习 7.5 练习 7.5 在你的Person类中提供一些操作使其能够返回姓名和住址。这些函数是否应该是const的呢?解释原因。 环境:Linux Ubuntu(云服务器) 工具:vim 解释 姓名大概…...
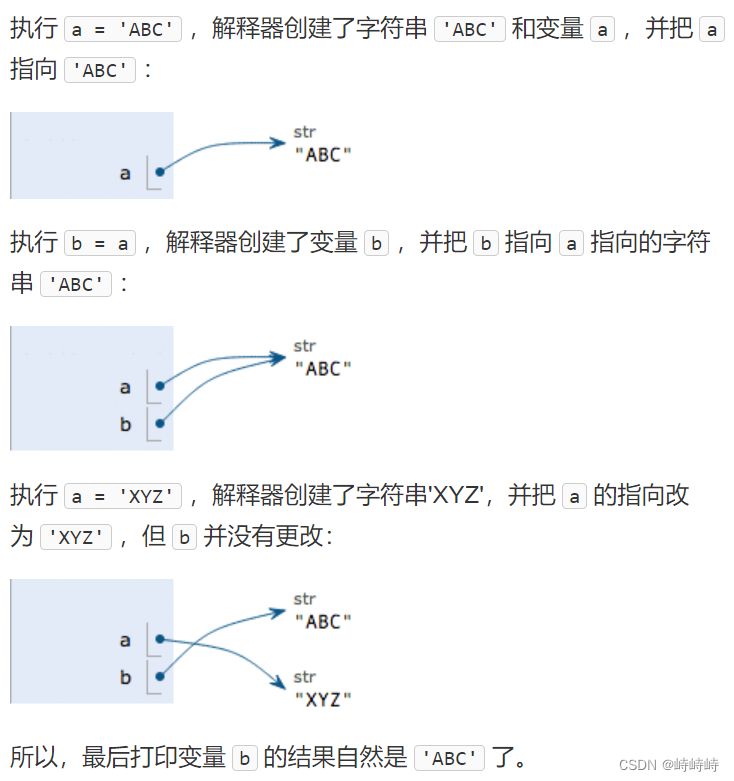
python系统学习Day2
section3 python Foudamentals part one:data types and variables 数据类型:整数、浮点数、字符串、布尔值、空值 #整型,没有大小限制 >>>9 / 3 #3.0 >>>10 // 3 #3 地板除 >>>10 % 3 #1 取余#浮点型ÿ…...

学习笔记——ENM模拟
学习笔记——ENM模拟 文章目录 前言一、文献一1. 材料与方法1.1. 大致概念1.2. 生态模型的构建1.2.1. 数据来源:1.2.2. 数据处理:1.2.3. 模型参数优化: 1.3. 适生情况预测1.3.1. 预测模型构建1.3.2. 适生区划分 1.4. 模型的评估与验证 2. 结果…...

数值类型的运算方式总结
提纲1:常见的位运算使用场景 提纲2:整数类型运算时的类型溢出问题,产生原因以及解决办法 提纲3:浮点类型运算时的精度丢失问题,产生原因以及解决办法 数值类型(6种)分为: 整型&…...

【Redis快速入门】Redis三种集群搭建配置(主从集群、哨兵集群、分片集群)
个人名片: 🐼作者简介:一名大三在校生,喜欢AI编程🎋 🐻❄️个人主页🥇:落798. 🐼个人WeChat:hmmwx53 🕊️系列专栏:🖼️…...

[嵌入式系统-14]:常见实时嵌入式操作系统比较:RT-Thread、uC/OS-II和FreeRTOS、Linux
目录 一、实时嵌入式操作系统 1.1 概述 1.2 什么“实时” 1.3 什么是硬实时和软实时 1.4 什么是嵌入式 1.5 什么操作系统 二、常见重量级操作系统 三、常见轻量级嵌入式操作系统 3.1 概述 3.2 FreeRTOS 3.3 uC/OS-II 3.4 RT-Thread 3.5 RT-Thread、uC/OS-II、Free…...
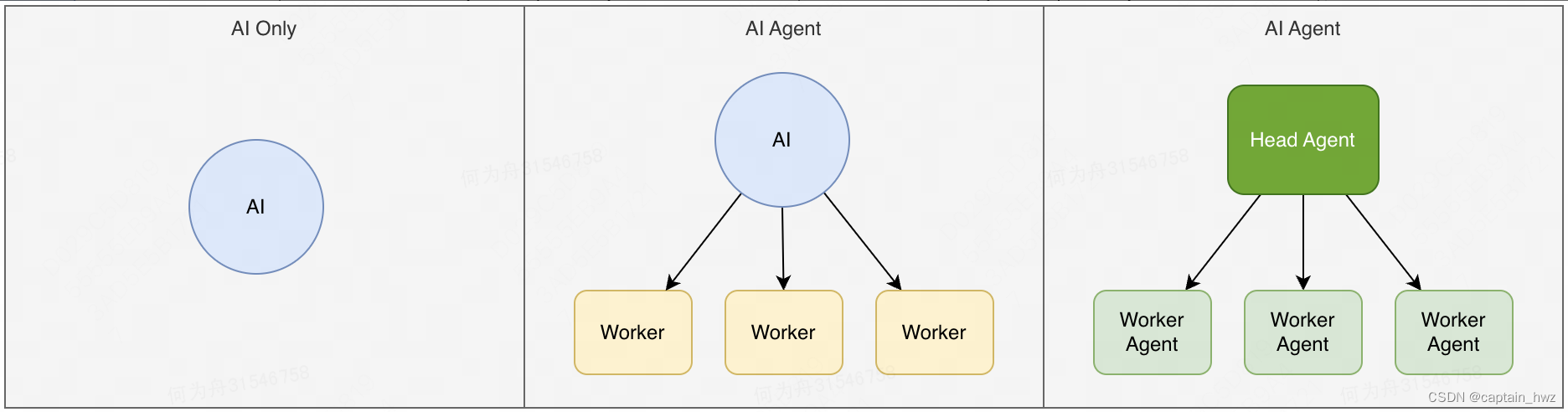
基于AI Agent探讨:安全领域下的AI应用范式
先说观点:关于AI应用,通常都会聊准召。但在安全等模糊标准的场景下,事实上不存在准召的定义。因此,AI的目标应该是尽可能的“像人”。而想要评价有多“像人”,就先需要将人的工作数字化。而AI Agent是能够将数字化、自…...
Stable Diffusion 模型下载:ToonYou(平涂卡通)
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十...
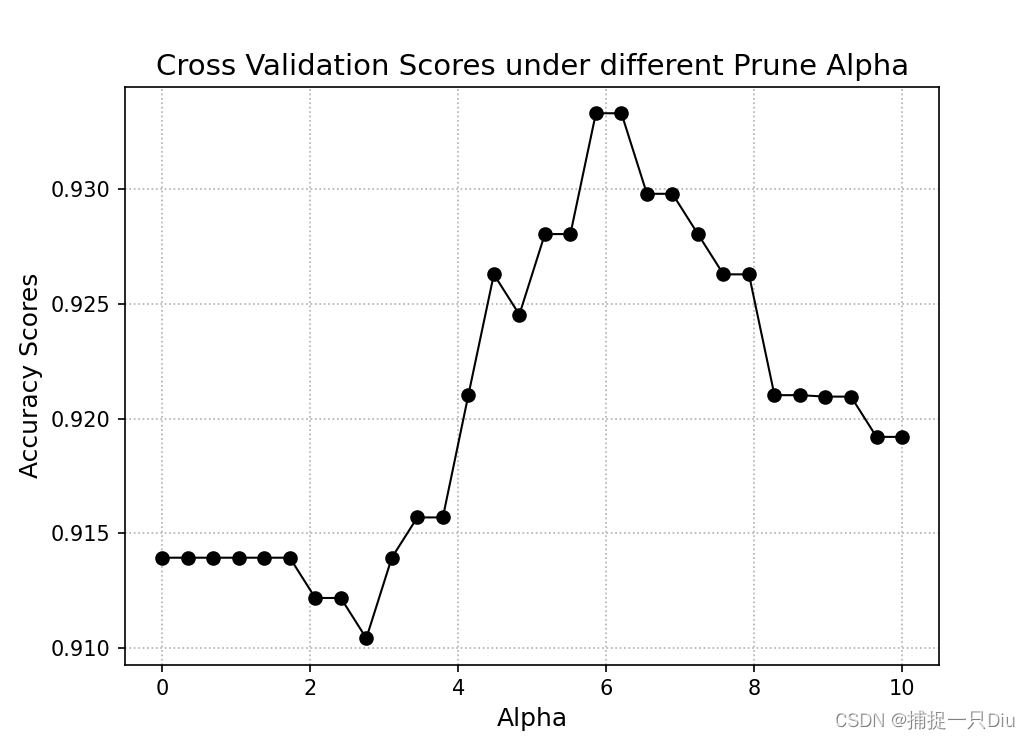
机器学习:分类决策树(Python)
一、各种熵的计算 entropy_utils.py import numpy as np # 数值计算 import math # 标量数据的计算class EntropyUtils:"""决策树中各种熵的计算,包括信息熵、信息增益、信息增益率、基尼指数。统一要求:按照信息增益最大、信息增益率…...

红队打靶练习:HACK ME PLEASE: 1
信息收集 1、arp ┌──(root㉿ru)-[~/kali] └─# arp-scan -l Interface: eth0, type: EN10MB, MAC: 00:0c:29:69:c7:bf, IPv4: 192.168.61.128 Starting arp-scan 1.10.0 with 256 hosts (https://github.com/royhills/arp-scan) 192.168.61.2 00:50:56:f0:df:20 …...
《VulnHub》GoldenEye:1
title: 《VulnHub》GoldenEye:1 date: 2024-02-16 14:53:49 updated: 2024-02-16 15:08:49 categories: WriteUp:Cyber-Range excerpt: 主机发现、目标信息扫描、源码 js 文件泄露敏感信息、hydra 爆破邮件服务(pop3)、邮件泄露敏…...
html的表格标签
html的表格标签 table标签:表示整个表格tr:表示表格的一行td:表示一个单元格th:表示表头单元格.会居中加粗thead:表格的头部区域 (注意和th区分,范围是比th要大的).tbody:表格得到主体区域. table包含tr , tr包含td或者th. 表格标签有一些属性,可以用于设置大小边…...
2022省赛真题:展开你的扇子)
蓝桥杯(Web大学组)2022省赛真题:展开你的扇子
思路: transform-origin: center bottom;使盒子旋转时,以底部的中心为坐标原点(题目已给出) 对每个盒子使用transform: rotate();实现旋转 笔记: 设置悬浮旋转时, #box div:hover #item6{ } 为什…...
复习基础知识1
局部变量 写程序时,程序员经常会用到局部变量 汇编中寄存器、栈,可写区段、堆,函数的局部变量该存在哪里呢? 注意:局部变量有易失性 一旦函数返回,则所有局部变量会失效。 考虑到这种特性,人们…...

java8-用流收集数据-6
本章内容口用co1lectors类创建和使用收集器 口将数据流归约为一个值 口汇总:归约的特殊情况 数据分组和分区口 口 开发自己的自定义收集器 我们在前一章中学到,流可以用类似于数据库的操作帮助你处理集合。你可以把Java8的流看作花哨又懒惰的数据集迭代器。它们…...

[前端开发] JavaScript基础知识 [上]
下篇:JavaScript基础知识 [下] JavaScript基础知识 [上] 引言语句、标识符和变量JavaScript引入注释与输出数据类型运算符条件语句与循环语句 引言 JavaScript是一种广泛应用于网页开发的脚本语言,具有重要的前端开发和部分后端开发的应用。通过JavaSc…...
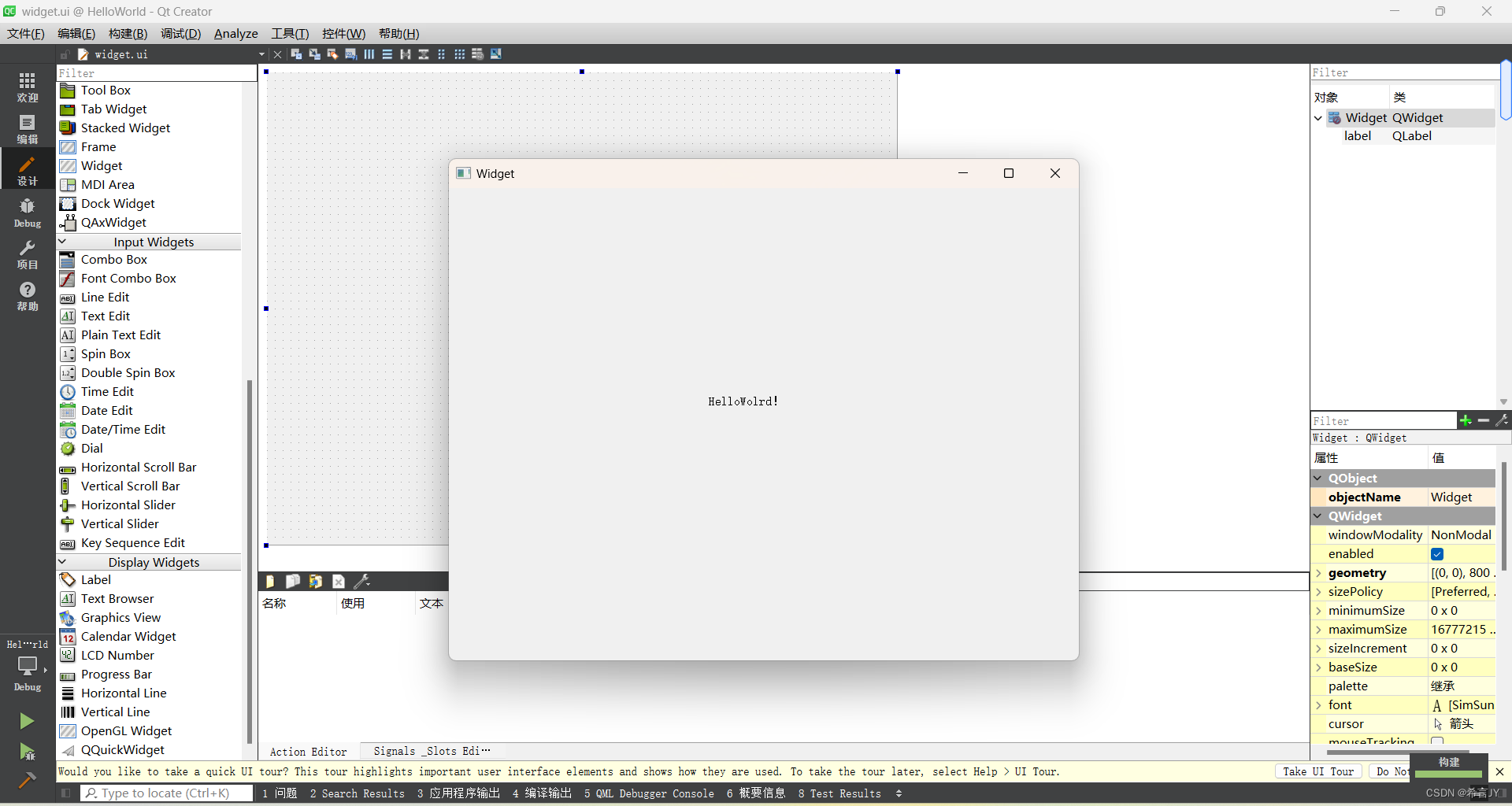
初识Qt | 从安装到编写Hello World程序
文章目录 1.前端开发简单分类2.Qt的简单介绍3.Qt的安装和环境配置4.创建简单的Qt项目 1.前端开发简单分类 前端开发,这里是一个广义的概念,不单指网页开发,它的常见分类 网页开发:前端开发的主要领域,使用HTML、CSS …...
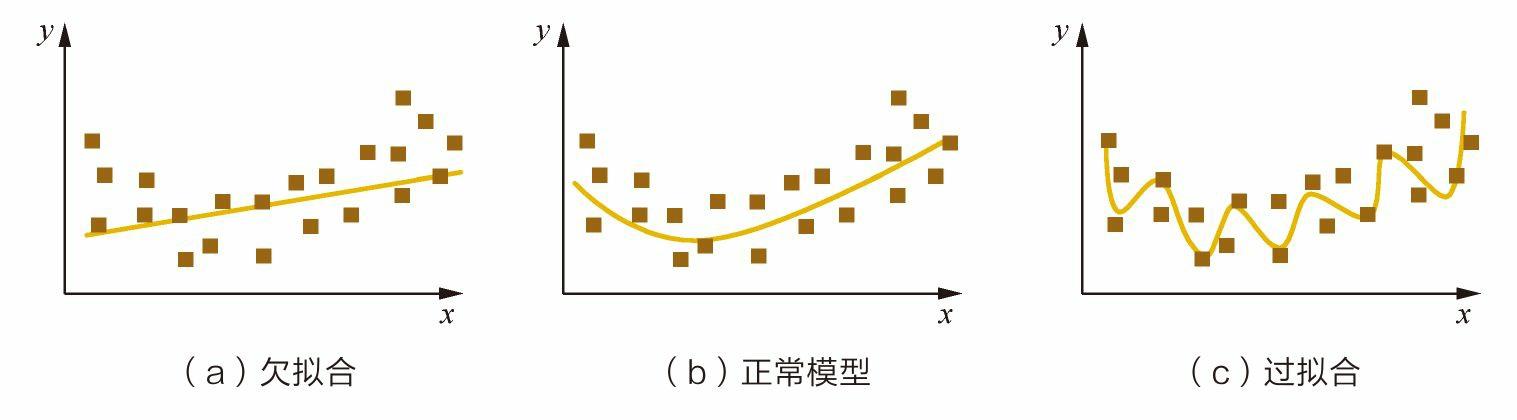
机器学习:过拟合和欠拟合的介绍与解决方法
过拟合和欠拟合的表现和解决方法。 其实除了欠拟合和过拟合,还有一种是适度拟合,适度拟合就是我们模型训练想要达到的状态,不过适度拟合这个词平时真的好少见。 过拟合 过拟合的表现 模型在训练集上的表现非常好,但是在测试集…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
