【图论经典题目讲解】CF786B - Legacy 一道线段树优化建图的经典题目
C F 786 B − L e g a c y \mathrm{CF786B - Legacy} CF786B−Legacy
D e s c r i p t i o n \mathrm{Description} Description
给定 1 1 1 张 n n n 个点的有向图,初始没有边,接下来有 q q q 次操作,形式如下:
1 u v w表示从 u u u 向 v v v 连接 1 1 1 条长度为 w w w 的有向边2 u l r w表示从 u u u 向 i i i( i ∈ [ l , r ] i\in [l,r] i∈[l,r])连接 1 1 1 条长度为 w w w 的有向边3 u l r w表示从 i i i( i ∈ [ l , r ] i\in [l,r] i∈[l,r])向 u u u 连接 1 1 1 条长度为 w w w 的有向边
输出从 S S S 点到 i i i 点( i ∈ [ 1 , n ] i\in [1,n] i∈[1,n])的最短路长度。
S o l u t i o n \mathrm{Solution} Solution
观察可知,最多会建立 1 0 5 × 1 0 5 = 1 0 10 10^5\times 10^5 = 10^{10} 105×105=1010 条边,故必定超时。
此时,需要使用 线段树优化建图,这里展开简单说一下:
对于 1 1 1 棵存储点为 1 ∼ 4 1\sim 4 1∼4 的线段树,形式如下:
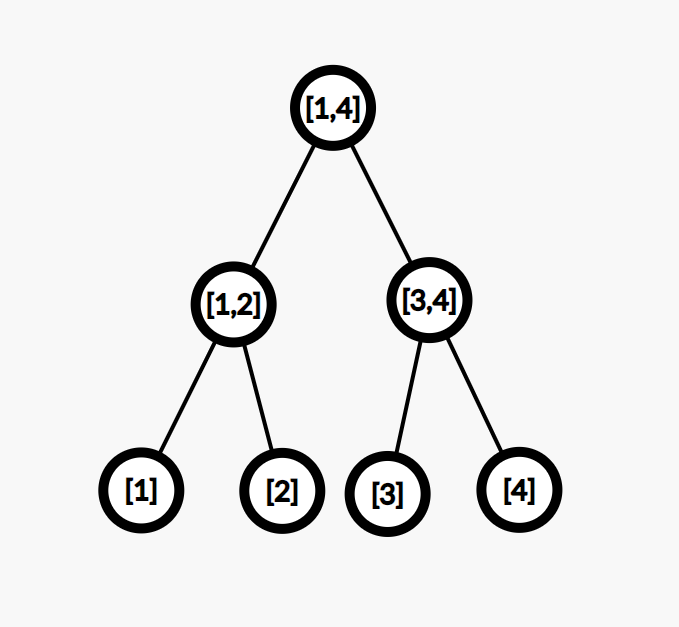
如果当前为 2 2 2 操作,且为 1 ∼ 3 1\sim 3 1∼3 每个点连向 4 4 4,权值为 10 10 10,操作如下所示:
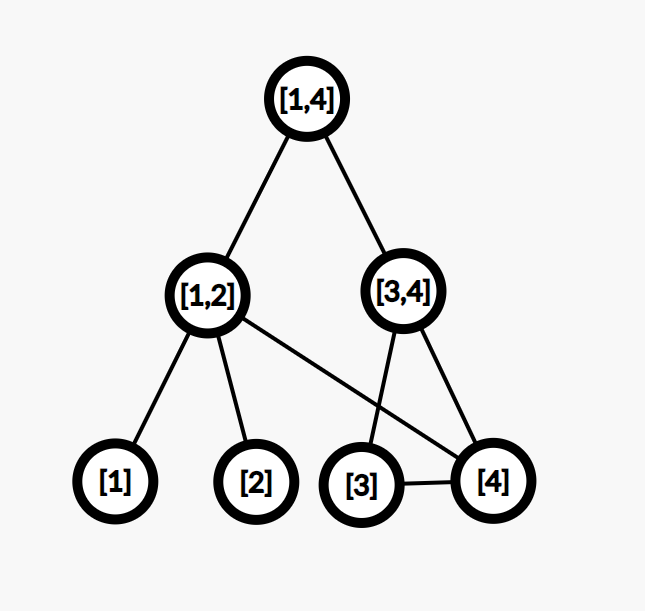
即,将区间 1 ∼ 2 1\sim 2 1∼2 和 3 ∼ 3 3\sim 3 3∼3 连向 4 4 4 即可,不过此时发现,图中为有向图,而现在是无向图所以我们要对于图中的每一条边标记方向和权值(这里线段树就是一张图,叶子节点就是我们的 1 ∼ n 1\sim n 1∼n 节点)
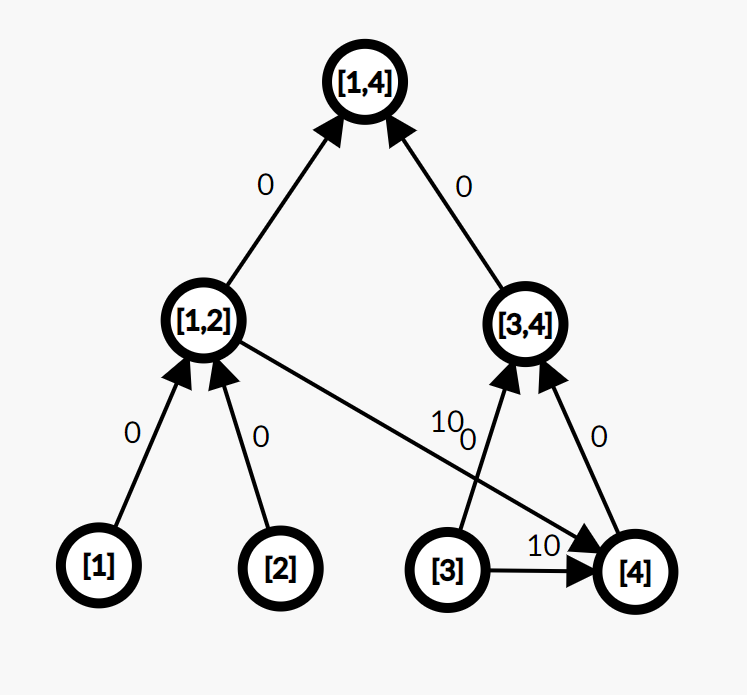
其中,为何线段树上的边方向都为向父亲节点?那是因为 1 1 1, 2 2 2 号点只有这样才能顺着边走到 4 4 4 号节点,对于为何权值设为 0 0 0,因为这是 1 1 1 条虚边(不存在的),不能对最短路做出任何贡献。
不过,上文是区间连节点,当是节点连区间的时候(操作 3 3 3)边都是正好反着的,所以再建 1 1 1 棵线段树即可(不过没必要真的去再建 1 1 1 棵,具体见代码)
C o d e Code Code
#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int SIZE = 4e6 + 10, SIZE2 = 1e6 + 10;int N, Q, S;
int h[SIZE2], e[SIZE], ne[SIZE], w[SIZE], idx;
int Id[2], Dist[SIZE2], Vis[SIZE2];
struct Segment
{int l, r;int L, R;
}Tree[SIZE2 << 2];void add(int a, int b, int c)
{e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}int Build(int l, int r, int Sd, int k)
{if (l == r){Tree[l] = {l, l};return l;}int P = ++ Id[k];Tree[P] = {l, r};int mid = l + r >> 1;Tree[P].L = Build(l, mid, Sd, k), Tree[P].R = Build(mid + 1, r, Sd, k);if (!Sd) add(Tree[P].L, P, 0), add(Tree[P].R, P, 0);else add(P, Tree[P].L, 0), add(P, Tree[P].R, 0);return P;
}void Add(int u, int l, int r, int p, int w, int Sd)
{if (Tree[u].l >= l && Tree[u].r <= r){if (!Sd) add(u, p, w);else add(p, u, w);return;}int mid = Tree[u].l + Tree[u].r >> 1;if (mid >= l) Add(Tree[u].L, l, r, p, w, Sd);if (mid < r) Add(Tree[u].R, l, r, p, w, Sd);
}void Dijkstra(int S)
{memset(Dist, 0x3f, sizeof Dist);memset(Vis, 0, sizeof Vis);priority_queue<PII, vector<PII>, greater<PII>> Heap;Heap.push({0, S}), Dist[S] = 0;while (Heap.size()){auto Tmp = Heap.top();Heap.pop();int u = Tmp.second;if (Vis[u]) continue;Vis[u] = 1;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (Dist[j] > Dist[u] + w[i]){Dist[j] = Dist[u] + w[i];Heap.push({Dist[j], j});}}}
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);memset(h, -1, sizeof h);cin >> N >> Q >> S;if (N == 1){cout << 0 << endl;return 0;}Id[0] = N;Build(1, N, 0, 0);Id[1] = Id[0];Build(1, N, 1, 1);while (Q --){int Op, v, u, l, r, w;cin >> Op >> u;if (Op == 1){cin >> v >> w;add(u, v, w);}else if (Op == 2){cin >> l >> r >> w;Add(Id[0] + 1, l, r, u, w, 1);}else{cin >> l >> r >> w;Add(N + 1, l, r, u, w, 0);}}Dijkstra(S);for (int i = 1; i <= N; i ++)if (Dist[i] >= 1e18) cout << -1 << " ";else cout << Dist[i] << " ";return 0;
}
相关文章:

【图论经典题目讲解】CF786B - Legacy 一道线段树优化建图的经典题目
C F 786 B − L e g a c y \mathrm{CF786B - Legacy} CF786B−Legacy D e s c r i p t i o n \mathrm{Description} Description 给定 1 1 1 张 n n n 个点的有向图,初始没有边,接下来有 q q q 次操作,形式如下: 1 u v w 表示…...

【AIGC】Stable Diffusion的采样器入门
在 Stable Diffusion 中,采样器(Sampler)是指用于生成图像的一种技术或方法,它决定了模型如何从潜在空间中抽样并生成图像。采样器在生成图像的过程中起着重要作用,影响着生成图像的多样性、质量和创造性。以下是对 St…...
【Python】通过conda安装Python的IDE
背景 系统:win11 软件:anaconda Navigator 问题现象:①使用Navigator安装jupyter notebook以及Spyder IDE 一直转圈。②然后进入anaconda prompt执行conda install jupyter notebook一直卡在Solving environment/-\。 类似问题: …...

基于HTML5实现动态烟花秀效果(含音效和文字)实战
目录 前言 一、烟花秀效果功能分解 1、功能分解 2、界面分解 二、HTML功能实现 1、html界面设计 2、背景音乐和燃放触发 3、燃放控制 4、对联展示 5、脚本引用即文本展示 三、脚本调用及实现 1、烟花燃放 2、燃放响应 3、烟花canvas创建 4、燃放声音控制 5、实际…...

「数据结构」栈和队列
栈 栈的基本概念 定义 栈是只允许在一端进行插入或删除操作的线性表栈顶:线性表允许进行插入删除的那一端栈底:固定的,不允许进行插入和删除的另一端空栈:不含任何元素特点:后进先出(LIFO) 基…...

【机器学习笔记】5 机器学习实践
数据集划分 子集划分 训练集(Training Set):帮助我们训练模型,简单的说就是通过训练集的数据让我们确定拟合曲线的参数。 验证集(Validation Set):也叫做开发集( Dev Set …...

C++ //练习 7.5 在你的Person类中提供一些操作使其能够返回姓名和住址。这些函数是否应该是const的呢?解释原因。
C Primer(第5版) 练习 7.5 练习 7.5 在你的Person类中提供一些操作使其能够返回姓名和住址。这些函数是否应该是const的呢?解释原因。 环境:Linux Ubuntu(云服务器) 工具:vim 解释 姓名大概…...
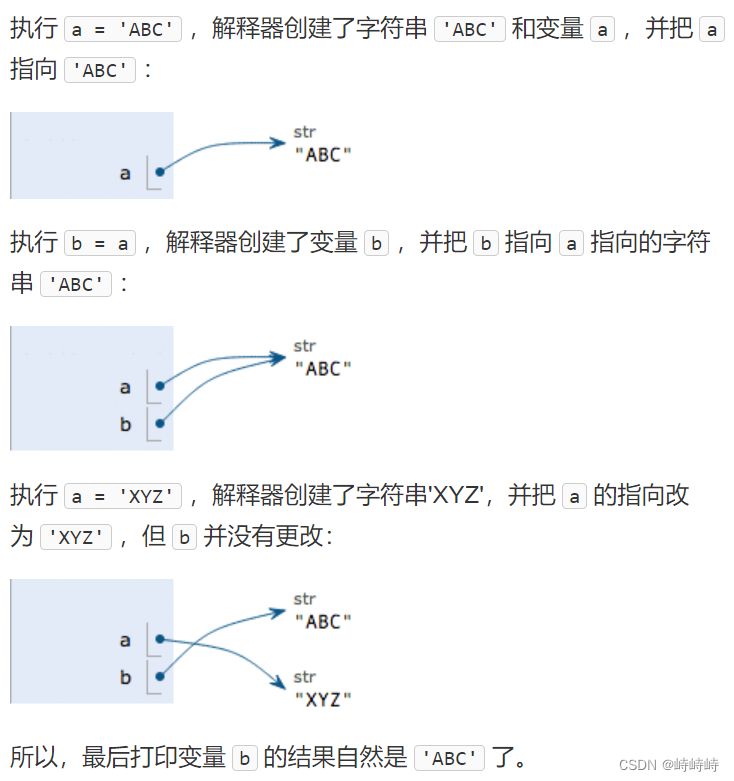
python系统学习Day2
section3 python Foudamentals part one:data types and variables 数据类型:整数、浮点数、字符串、布尔值、空值 #整型,没有大小限制 >>>9 / 3 #3.0 >>>10 // 3 #3 地板除 >>>10 % 3 #1 取余#浮点型ÿ…...

学习笔记——ENM模拟
学习笔记——ENM模拟 文章目录 前言一、文献一1. 材料与方法1.1. 大致概念1.2. 生态模型的构建1.2.1. 数据来源:1.2.2. 数据处理:1.2.3. 模型参数优化: 1.3. 适生情况预测1.3.1. 预测模型构建1.3.2. 适生区划分 1.4. 模型的评估与验证 2. 结果…...

数值类型的运算方式总结
提纲1:常见的位运算使用场景 提纲2:整数类型运算时的类型溢出问题,产生原因以及解决办法 提纲3:浮点类型运算时的精度丢失问题,产生原因以及解决办法 数值类型(6种)分为: 整型&…...

【Redis快速入门】Redis三种集群搭建配置(主从集群、哨兵集群、分片集群)
个人名片: 🐼作者简介:一名大三在校生,喜欢AI编程🎋 🐻❄️个人主页🥇:落798. 🐼个人WeChat:hmmwx53 🕊️系列专栏:🖼️…...

[嵌入式系统-14]:常见实时嵌入式操作系统比较:RT-Thread、uC/OS-II和FreeRTOS、Linux
目录 一、实时嵌入式操作系统 1.1 概述 1.2 什么“实时” 1.3 什么是硬实时和软实时 1.4 什么是嵌入式 1.5 什么操作系统 二、常见重量级操作系统 三、常见轻量级嵌入式操作系统 3.1 概述 3.2 FreeRTOS 3.3 uC/OS-II 3.4 RT-Thread 3.5 RT-Thread、uC/OS-II、Free…...
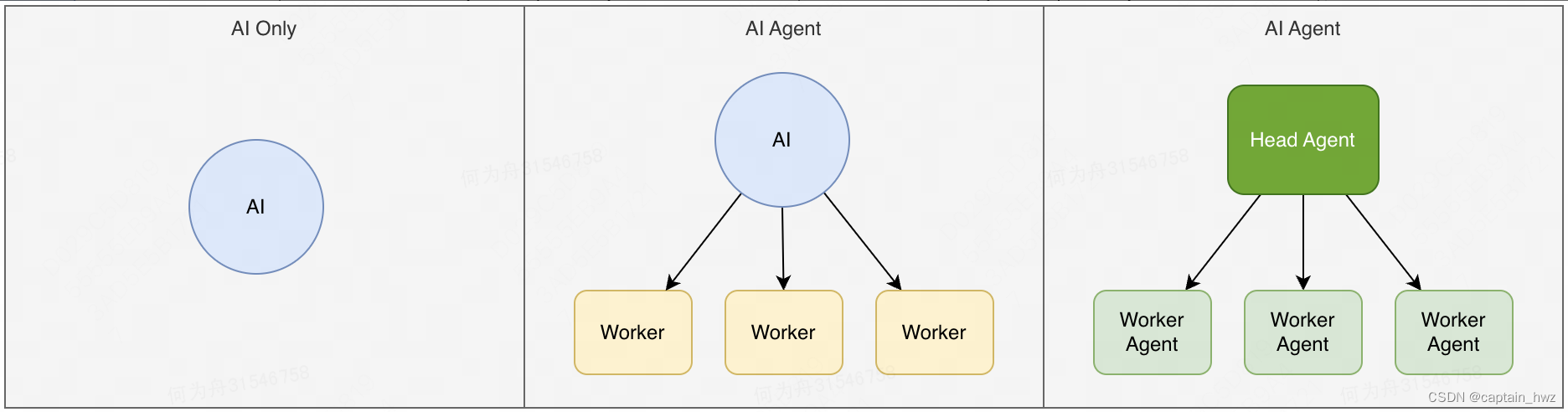
基于AI Agent探讨:安全领域下的AI应用范式
先说观点:关于AI应用,通常都会聊准召。但在安全等模糊标准的场景下,事实上不存在准召的定义。因此,AI的目标应该是尽可能的“像人”。而想要评价有多“像人”,就先需要将人的工作数字化。而AI Agent是能够将数字化、自…...
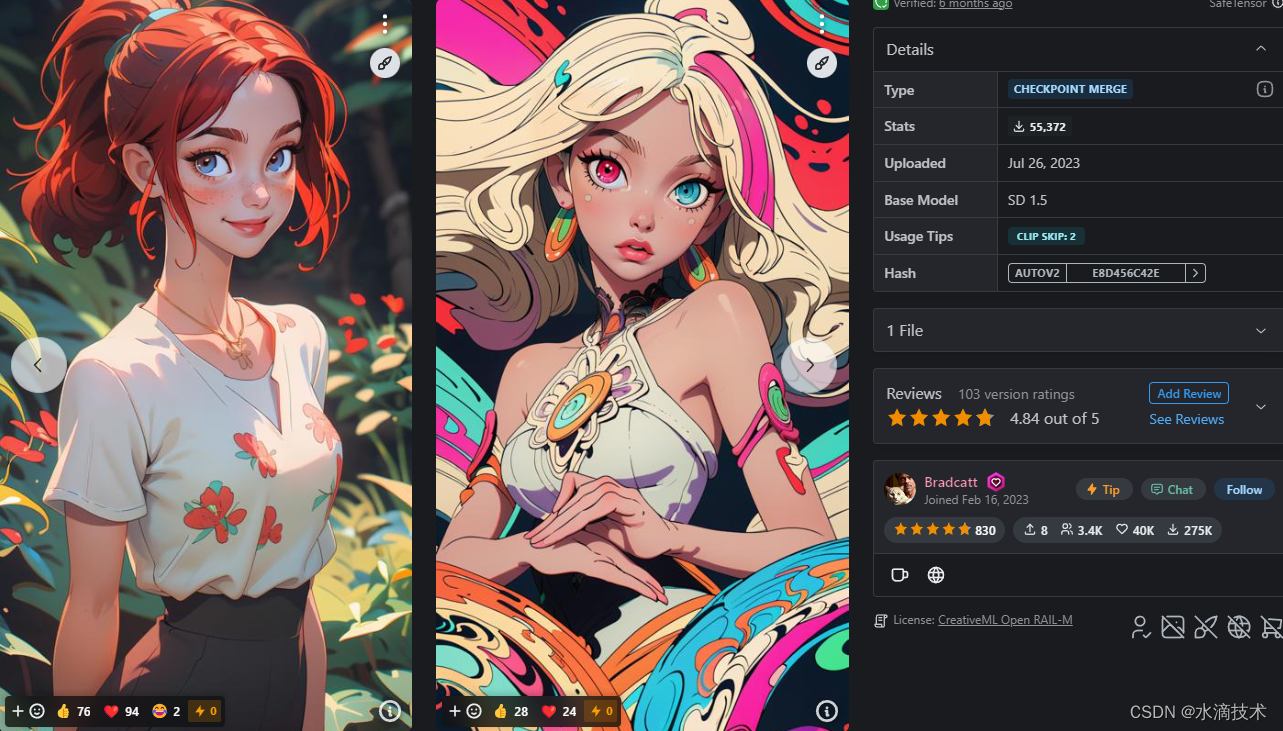
Stable Diffusion 模型下载:ToonYou(平涂卡通)
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十...
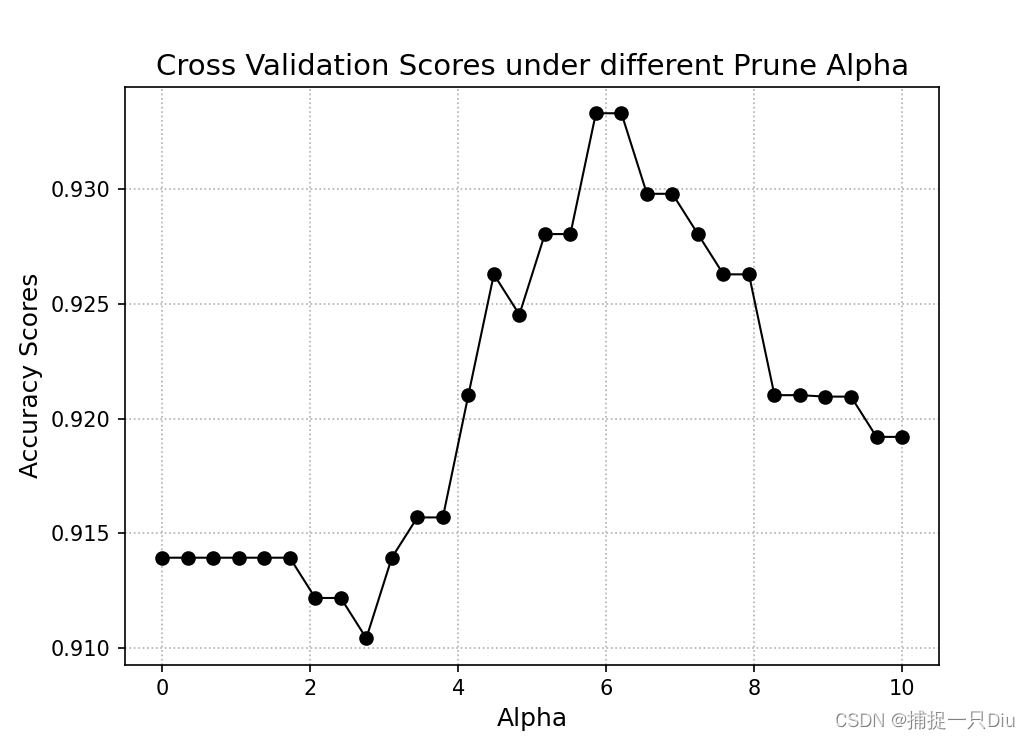
机器学习:分类决策树(Python)
一、各种熵的计算 entropy_utils.py import numpy as np # 数值计算 import math # 标量数据的计算class EntropyUtils:"""决策树中各种熵的计算,包括信息熵、信息增益、信息增益率、基尼指数。统一要求:按照信息增益最大、信息增益率…...

红队打靶练习:HACK ME PLEASE: 1
信息收集 1、arp ┌──(root㉿ru)-[~/kali] └─# arp-scan -l Interface: eth0, type: EN10MB, MAC: 00:0c:29:69:c7:bf, IPv4: 192.168.61.128 Starting arp-scan 1.10.0 with 256 hosts (https://github.com/royhills/arp-scan) 192.168.61.2 00:50:56:f0:df:20 …...
《VulnHub》GoldenEye:1
title: 《VulnHub》GoldenEye:1 date: 2024-02-16 14:53:49 updated: 2024-02-16 15:08:49 categories: WriteUp:Cyber-Range excerpt: 主机发现、目标信息扫描、源码 js 文件泄露敏感信息、hydra 爆破邮件服务(pop3)、邮件泄露敏…...
html的表格标签
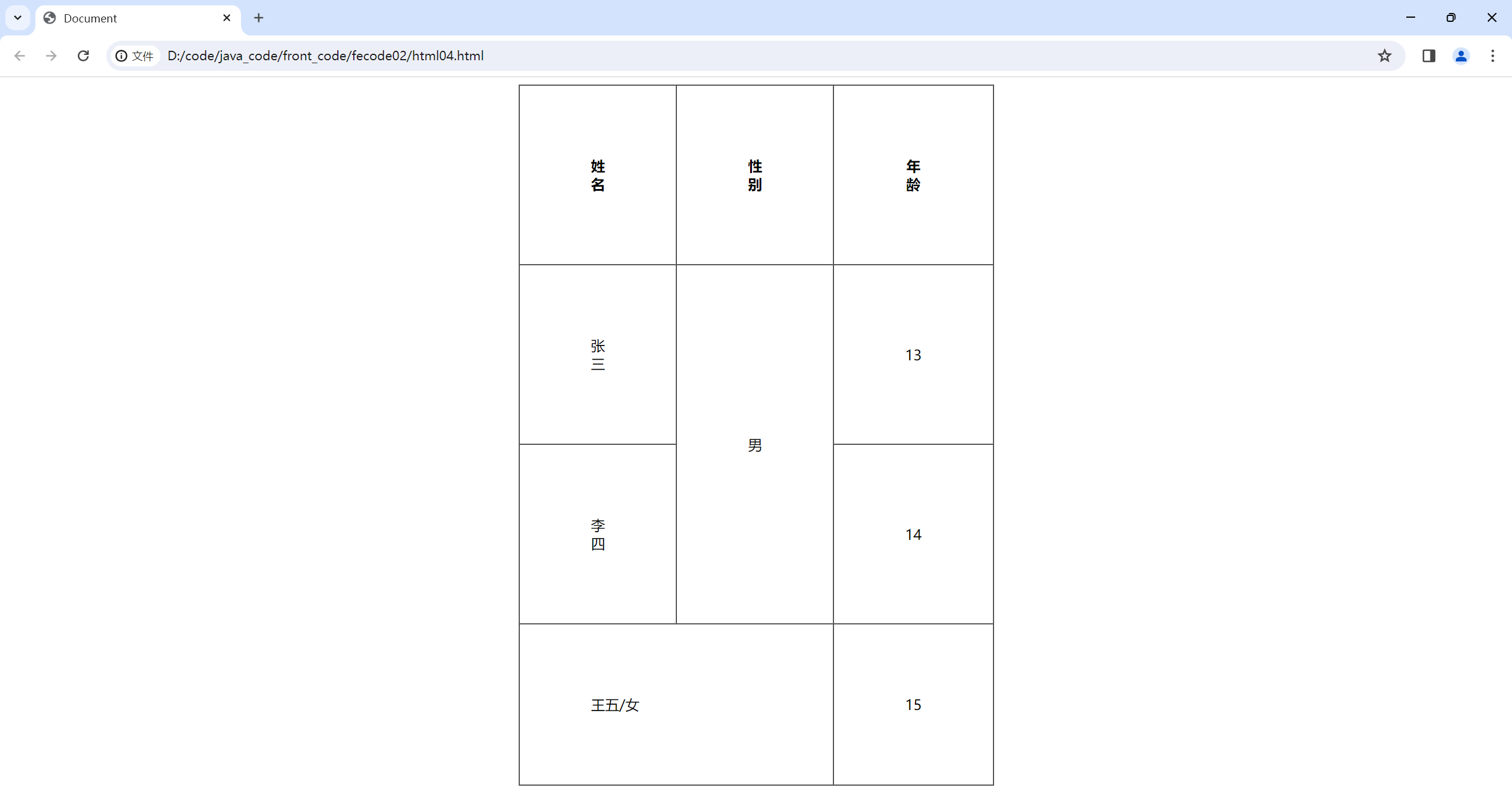
html的表格标签 table标签:表示整个表格tr:表示表格的一行td:表示一个单元格th:表示表头单元格.会居中加粗thead:表格的头部区域 (注意和th区分,范围是比th要大的).tbody:表格得到主体区域. table包含tr , tr包含td或者th. 表格标签有一些属性,可以用于设置大小边…...
2022省赛真题:展开你的扇子)
蓝桥杯(Web大学组)2022省赛真题:展开你的扇子
思路: transform-origin: center bottom;使盒子旋转时,以底部的中心为坐标原点(题目已给出) 对每个盒子使用transform: rotate();实现旋转 笔记: 设置悬浮旋转时, #box div:hover #item6{ } 为什…...
复习基础知识1
局部变量 写程序时,程序员经常会用到局部变量 汇编中寄存器、栈,可写区段、堆,函数的局部变量该存在哪里呢? 注意:局部变量有易失性 一旦函数返回,则所有局部变量会失效。 考虑到这种特性,人们…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
