dp模型——状态机模型C++详解
状态机定义
状态机顾名思义跟状态有关系,但到底有什么关系呢。在实际解决的时候,通常把状态想成节点,状态的转换想成有向边的有向图,我们来举个例子。
相信大家都玩过类似枪战的游戏(没玩过的也听说过吧), 他的每一个人物基本都有几个状态:站立,蹲下,跑步和射击。这就可以构成一个简单的状态机图了。
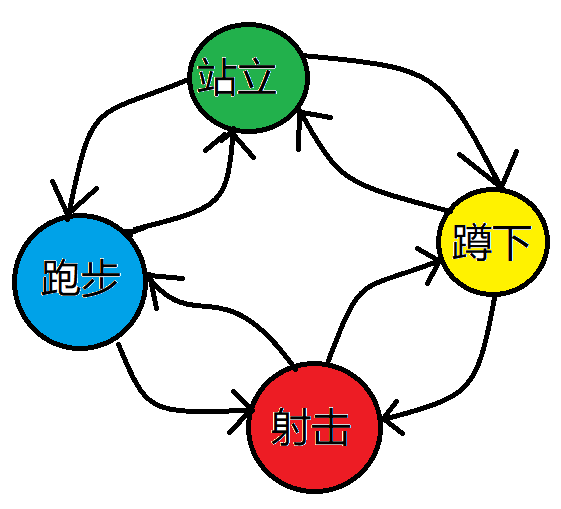
状态机模型
我们拿例题来分析一下。
例题
1049. 大盗阿福
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T,表示一共有 T组数据。
接下来的每组数据,第一行是一个整数 N,表示一共有 N家店铺。
第二行是 N个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过1000。
输出格式
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
数据范围
1≤T≤50,
1≤N≤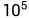
输入样例:
2
3
1 8 2
4
10 7 6 14输出样例:
8
24样例解释
对于第一组样例,阿福选择第2家店铺行窃,获得的现金数量为8。
对于第二组样例,阿福选择第1和4家店铺行窃,获得的现金数量为10+14=24。
这道题的大意就是,有t组数据,每个有n个超市,告诉你每一家的价钱,不能盗窃相邻的超市。
计算大盗能获得的最大利益。
解题思路
这道题有两种解法,第一种是普通的线性dp,第二种是状态机dp。
第一种
用f[i]表示前i家商店阿福可以获得的最大价值。
对于第i次选择,只能选偷或者不偷,偷就是f[i - 2] + w[i], 不偷就是f[i - 1]。
状态转移方程就是:
f[i] = max(f[i - 2] + w[i], f[i - 1]);完整ac代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, INF = 1e9;
int t, n;
int w[N], f[N];
int main() {scanf("%d", &t);while(t--) {scanf("%d", &n);for(int i = 1; i <= n; i++) scanf("%d", &w[i]);memset(f, -INF, sizeof f);f[0] = 0;for(int i = 1; i <= n; i++) f[i] = max(f[i - 2] + w[i], f[i - 1]);printf("%d\n", f[n]);}return 0;
}第二种就是今天讲到的状态机了,对于第i个超市,可以选择偷或者不偷,我们用1表示偷,0表示不偷(都是当前的超市)。
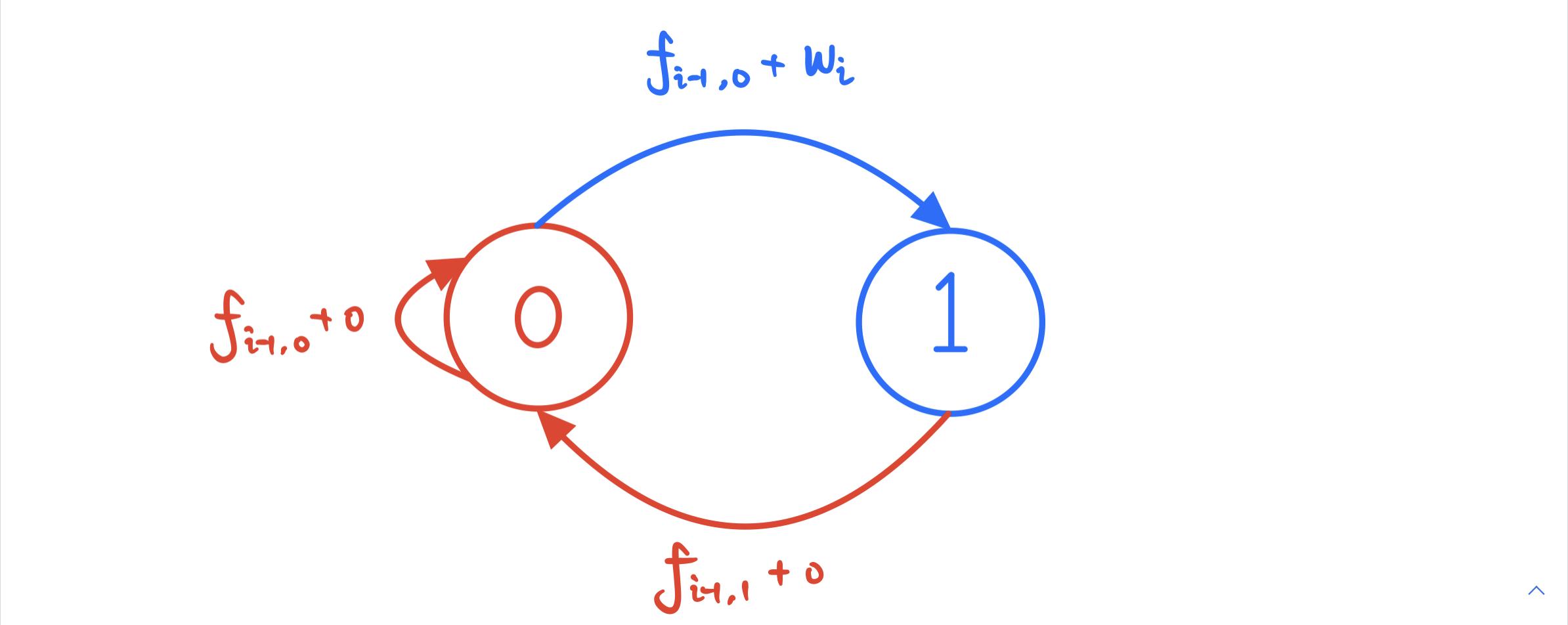
状态转移方程就是:
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + w[i];ac代码如下:
#include <bits/stdc++.h>
using namespace std;
#define read(a) scanf("%d", &a);
const int N = 1e5 + 10, INF = 1e9;
int t, n;
int w[N], f[N][2];
int main() {read(t);while(t--) {read(n);for(int i = 1; i <= n; i++) read(w[i]);f[0][0] = 0, f[0][1] = -INF;for(int i = 1; i <= n; i++) {f[i][0] = max(f[i - 1][0], f[i - 1][1]);f[i][1] = f[i - 1][0] + w[i];}printf("%d\n", max(f[n][1], f[n][0]));}return 0;
}相关文章:

dp模型——状态机模型C++详解
状态机定义状态机顾名思义跟状态有关系,但到底有什么关系呢。在实际解决的时候,通常把状态想成节点,状态的转换想成有向边的有向图,我们来举个例子。相信大家都玩过类似枪战的游戏(没玩过的也听说过吧)&…...

1.4 条件概率与乘法公式
1.4.1 条件概率在实际问题中,除了直接考虑某事件 B 发生的概率P(B)外,有时还会碰到这样的问题,就是“在事件A 已经发生的条件下,事件B 发生的概率”。一般情况下,后概率与前一概率不同,为了区别,我们常把后者称为条件概率,记为P(B…...
VITA/PYTHON/LUPA families
Image Sensor Group Top to Bottom Portfolio in Industrial Imaging Machine Vision • Factory automation and inspection • Robotic vision • Biometrics High-End Surveillance • Aerial Surveillance • Intelligent Traffic Systems (ITS) • Mapping Medical and Sc…...

ChatGPT概述:从模型训练到基本应用的介绍
ChatGPT概述:从模型训练到基本应用的介绍 目录 本文是对ChatGPT的由来、训练过程以及实际落地场景的解释,主要内容包括如下三个方面: 1、ChatGPT是什么 2、ChatGPT的原理 3、ChatGPT的思考 4、ChatGPT的应用 ChatGPT是什么 ChatGPT可能是近…...

C语言实现扫雷【详细讲解+全部源码】
扫雷的实现1. 配置运行环境2. 扫雷游戏的初步实现2.1 建立扫雷分布模块2.2 创建名为board的二维数组并进行棋盘初始化2.3 打印棋盘3. 接下来该讨论的事情3.1 布置雷3.2 排查雷3.3 统计坐标周围有几个雷4. 完整扫雷游戏的实现4.1 game.h4.2 game.c4.3 扫雷.c1. 配置运行环境 本游…...

Vue2.0开发之——购物车案例-Goods组件封装-商品名称和图片(46)
一 概述 循环渲染Goods组件为Goods组件封装title属性为Goods组件封装pic属性 二 循环渲染Goods组件 2.1 App.vue中导入Goods组件 import Goods from /components/Goods/Goods.vue2.2 App.vue中注册Goods组件 components: {Header,Goods}2.3 循环渲染每一个商品的信息 <…...

0201基础-组件-React
1 组件和模块 1.1 模块 对外提供特定功能的js程序,一般就是一个js文件 为什么拆分模块呢?随着业务逻辑增加,代码越来越多,越来越复杂。作用:复用js,简化js,提高js运行效率 1.2 模块化 当应用…...

论文笔记 | Conducting research in marketing with quasi-experiments
这篇论文是Journal of Marketing上的论文,讲了使用准实验来进行论文研究的一些事项。外生性识别的来源、几种准实验方法的注意点还有内生性的解决。 这篇论文对于准实验或者是平常论文的展开有一个非常友善的指导功能,可以阅读~ 摘要:本文旨…...
)
有关Android导览(Android Navigation component)
文章目录小结有关Android导览(Android Navigation component)碰到的问题参考小结 在使用Android导览(Android Navigation component)碰到很多问题。解决了一些问题,但是“Skipped xxx frames! The application may be doing too much work on its main thread”这样…...
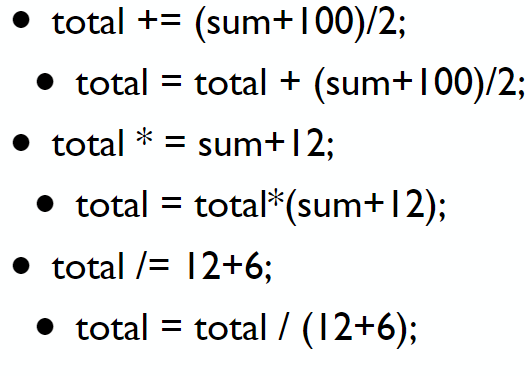
01 C语言计算
C语言计算 1、变量 用途:需要存放输入的数据 定义格式:数据类型 变量名(用于区分其他变量) 变量名格式:只能由字母/下划线/数字构成,首位不能是数字;且变量名不能是标识符 **变量赋值和初始…...
)
java单元测试简介(基于SpringBoot)
java单元测试简介(基于SpringBoot)mockitomock创建mock对象的另一种方式:Mockverifystubbing(存根)Spy(间谍)mock 静态方法mockito在springboot mock中的实战mockito 通常,在我们写单测时,会遇…...
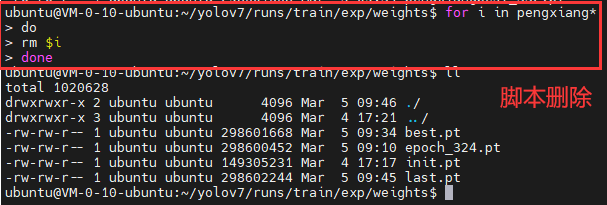
Linux常用命令操作
文件目录操作 查看文件列表 ls #输出列表信息 ls -l #输出详细列表信息 ls -a #输出隐藏文件 ls -la #输出包含的隐藏文件及详细信息 ll # ls-l的缩写rwx分别对应读取,写入,执行权限,前面有d代表是文件夹 创建文件 touch file.txt #创建…...

SpringCloud GateWay配置—TLS 和 SSL、Http超时配置
一、TLS 和 SSL网关可以按照通常的 Spring 服务器配置侦听 HTTPS 上的请求。 以下示例演示如何执行此操作:application.ymlserver:ssl:enabled: truekey-alias: scgkey-store-password: scg1234key-store: classpath:scg-keystore.p12key-store-type: PKCS12您可以将…...

python Django中的cookies和session会话保持技术
cookies和session都是为了保持会话状态而诞生的两个存储技术会话定义: 从打开浏览器访问一个网站,到关闭浏览器结束此次访问,称之为一次会话HTTP协议是无状态的,导致会话状态难以保持Cookies-定义 cookies是保存在客户端浏览器上的…...
vue3的v-model指令
1. 普通input输入框双向绑定 <template><!-- 1. 普通input输入框双向绑定 --><!-- 其实等价于:<input :modelValue"title" update:modelValue"newTitle>titlenewTitle"/> --><input type"text" v-mod…...

Matlab小波去噪——基于wden函数的去噪分析
文章目录一、问题描述二、代码问题1:原始信号加6分贝高斯白噪声问题2:确定合适的小波基函数问题3:确定最合适的阈值计算估计方法问题4:确定合适的分解层数问题5:实际信号去噪问题6:对比三、演示视频最后一、…...

分布式对象存储——Apache Hadoop Ozone
前言 本文隶属于专栏《大数据技术体系》,该专栏为笔者原创,引用请注明来源,不足和错误之处请在评论区帮忙指出,谢谢! 本专栏目录结构和参考文献请见大数据技术体系 1. 概述 Ozone是Apache Hadoop项目的子项目…...

Linux 和数据库笔记-03
今天主要内容数据库相关介绍数据库(软件)常见类型Navicat 工具基本使用常见的数据类型和约束(重点)SQL 语句的编写(表和数据)一. 数据库是什么?为什么学习数据库软件中产生的所有数据, 最终都要存储于数据库当中测试人员如果想要进行数据查询/数据校验, 就必须掌握对数据库的基…...
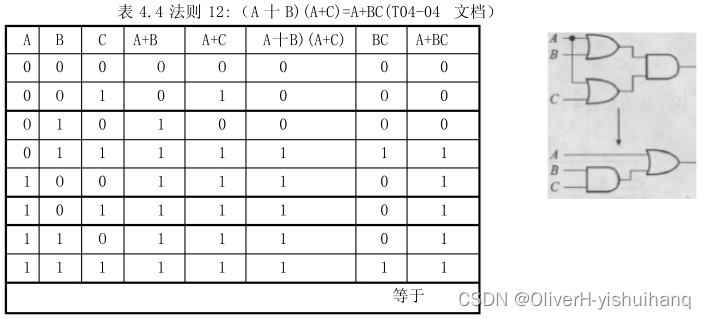
布尔定律---布尔代数的基本定律
一、单变量布尔定律 1、0-1定律 2、互补定律 3、重叠定律 4、还原定律 小结:或运算和与运算定律的差别在于:所有的“|”运算符换成“&”,运算结果为 0 换成 1。这就是对偶定律。它不仅是单逻辑变量的定律,而且对于所有布尔定…...

OSG三维渲染引擎编程学习之七十五:“第七章:OSG场景图形交互” 之 “7.6 多视图”
目录 第七章 OSG场景图形交互 7.6 多视图 7.6.1 多视图描述 7.6.2 多视图相机示例 第七章 OSG场景图形交互 作为一个成熟的三维渲染引擎,需...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
