【力扣】55.跳跃游戏、45.跳跃游戏Ⅱ
55.跳跃游戏
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
- 1 <= nums.length <= 104
- 0 <= nums[i] <= 105
解题方法
- C 贪心算法
/* 对于一个位置 target,只要存在一个位置 i 可以到达,* 并且下一步可以到达的最大长度为 nums[i],只要保证* i + nums[i] >= target,那么 target 便可到达。*/
#define MAX(a, b) ((a) > (b) ? (a) : (b))bool canJump(int* nums, int numsSize) {int target = 0;for (int i = 0; i < numsSize; i++) {if (i > target) {/* 当前位置不可到达 */return false;} else {/* 更新可以到达位置的最大值 */target = MAX(target, i + nums[i]);}}return true;
}
复杂度分析
时间复杂度为 O(n),其中 n 为数组的大小。
空间复杂度为 O(1),不需要额外的空间开销。
45.跳跃游戏Ⅱ
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
- 0 <= j <= nums[i]
- i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
- 1 <= nums.length <= 104
- 0 <= nums[i] <= 1000
- 题目保证可以到达
nums[n-1]
解题方案
- C 贪心算法
#define MAX(a, b) ((a) > (b) ? (a) : (b))int jump(int* nums, int numsSize) {int max_tg = 0; // 能跳跃到的最远位置int step = 0; // 跳跃次数int next_start = 0; // 下次起跳点for (int i = 0; i < numsSize - 1; i++) {max_tg = MAX(max_tg, i + nums[i]);if (i == next_start) {next_start = max_tg; // 更新起跳位置step++; // 跳跃计数}}return step;
}
复杂度分析
时间复杂度为 O(n),其中 nnn 是数组长度。
空间复杂度为 O(1)。
相关文章:

【力扣】55.跳跃游戏、45.跳跃游戏Ⅱ
55.跳跃游戏 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1&a…...

038—pandas 重采样线性插补
前言 在数据处理时,由于采集数据量有限,或者采集数据粒度过小,经常需要对数据重采样。在本例中,我们将实现一个类型超分辨率的操作。 思路: 首先将原始数据长度扩展为 3 倍,可以使用 loc[] 方法对索引扩…...

智慧工地源码 数字孪生可视化大屏 工地管理平台系统源码 多端展示(PC端、手机端、平板端)
智慧工地源码 数字孪生可视化大屏 工地管理平台系统源码 多端展示(PC端、手机端、平板端) 智慧工地系统多端展示(PC端、手机端、平板端);数字孪生可视化大屏,一张图掌握项目整体情况;使用轻量化模型,部署三…...
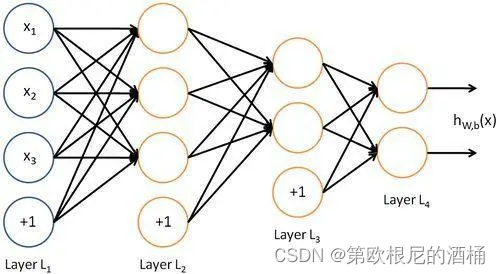
深度学习Top10算法之深度神经网络DNN
深度神经网络(Deep Neural Networks,DNN)是人工神经网络(Artificial Neural Networks,ANN)的一种扩展。它们通过模仿人脑的工作原理来处理数据和创建模式,广泛应用于图像识别、语音识别、自然语…...
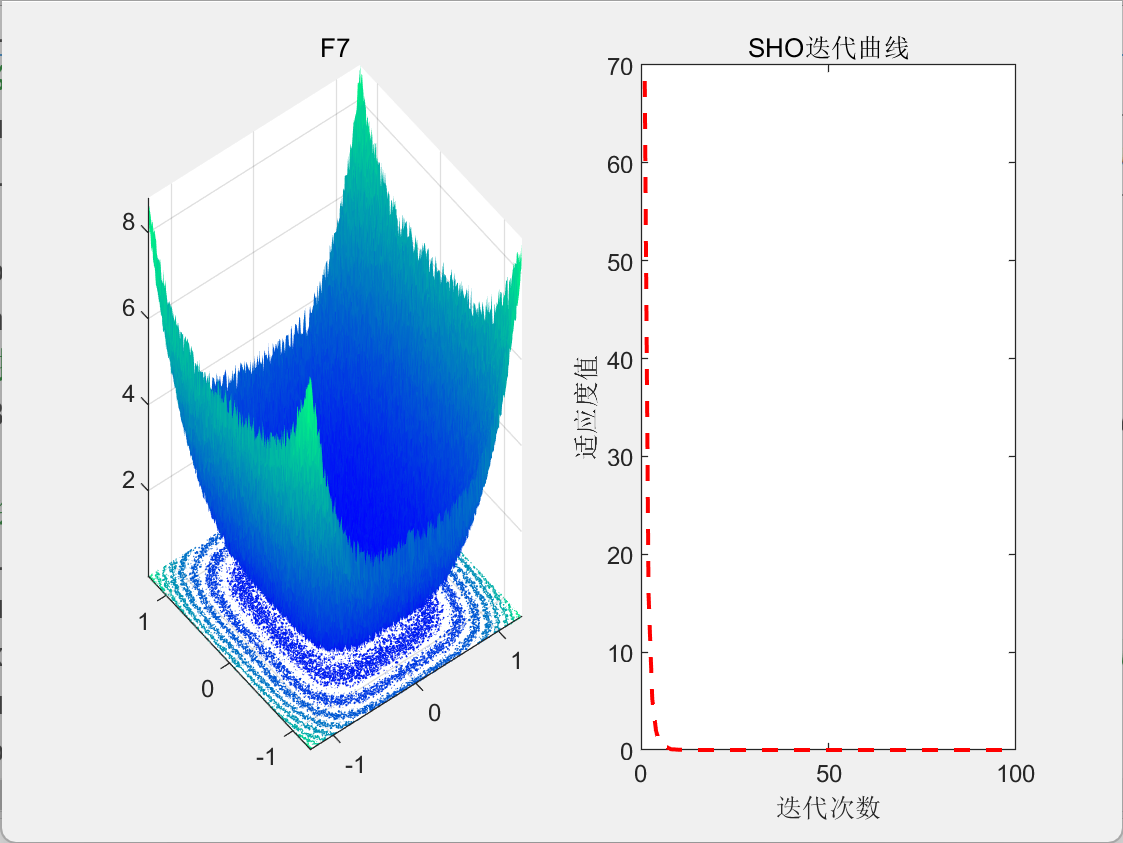
【智能算法】海马优化算法(SHO)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2022年,Zhao等人受到海马自然社会行为启发,提出了海马优化算法(Sea-horse Optimizer, SHO)。 2.算法原理 2.1算法思想 SHO模拟了海马群在自然界中的…...

AI大模型学习的伦理与社会影响
AI大模型学习 随着人工智能技术的快速发展,AI大模型学习成为当前热门研究领域之一。AI大模型学习是指基于大规模数据集和深度学习模型进行训练,以实现更高的准确性和复杂性。这些大模型已经在几乎所有领域都取得了显著的成就,包括自然语言处…...
记录些LangChain相关的知识
RAG的输出准确率 RAG的输出准确率 向量信息保留率 * 语义搜索准确率 * LLM准确率RAG的输出准确率由三个因素共同决定:向量信息保留率、语义搜索准确率以及LLM准确率。这三个因素是依次作用的,因此准确率实际上是它们的乘积。这意味着,任何一…...
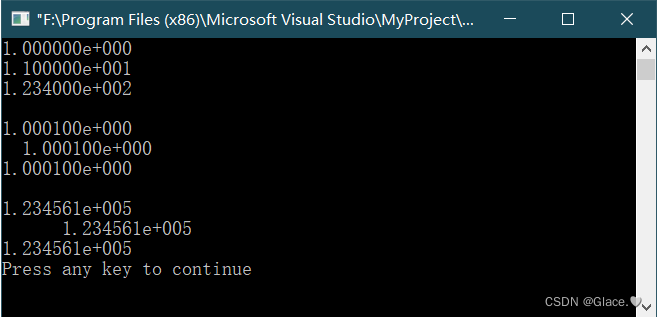
C语言例4-7:格式字符f的使用例子
%f,实型,小数部分为6位 代码如下: //格式字符f的使用例子 #include<stdio.h> int main(void) {float f 123.456;double d1, d2;d11111111111111.111111111;d22222222222222.222222222;printf("%f,%12f,%12.2f,%-12.2f,%.2f\n&qu…...

[蓝桥杯 2019 省 A] 修改数组
题目链接 [蓝桥杯 2019 省 A] 修改数组 题目描述 给定一个长度为 N N N 的数组 A [ A 1 , A 2 , A 3 , . . . , A N ] A [A_1, A_2, A_3, ...,A_N] A[A1,A2,A3,...,AN],数组中有可能有重复出现的整数。 现在小明要按以下方法将其修改为没有重复整数的…...

Git基础(25):Cherry Pick合并指定commit id的提交
文章目录 前言指定commit id合并使用TortoiseGit执行cherry-pick命令 前言 开发中,我们会存在多个分支开发的情况,比如dev,test, prod分支,dev分支在开发新功能,prod作为生产分支已发布。如果某个时候,我们…...

C语言结构体之位段
位段(节约内存),和王者段位联想记忆 位段是为了节约内存的。刚好和结构体相反。 那么什么是位段呢?我们现引入情景:我么如果要记录一个人是男是女,用数字0 1表示。我们发现只要一个bit内存就可以完成我们想…...

2016年认证杯SPSSPRO杯数学建模D题(第二阶段)NBA是否有必要设立四分线全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 D题 NBA是否有必要设立四分线 原题再现: NBA 联盟从 1946 年成立到今天,一路上经历过无数次规则上的变迁。有顺应民意、皆大欢喜的,比如 1973 年在技术统计中增加了抢断和盖帽数据;有应运而生、力…...
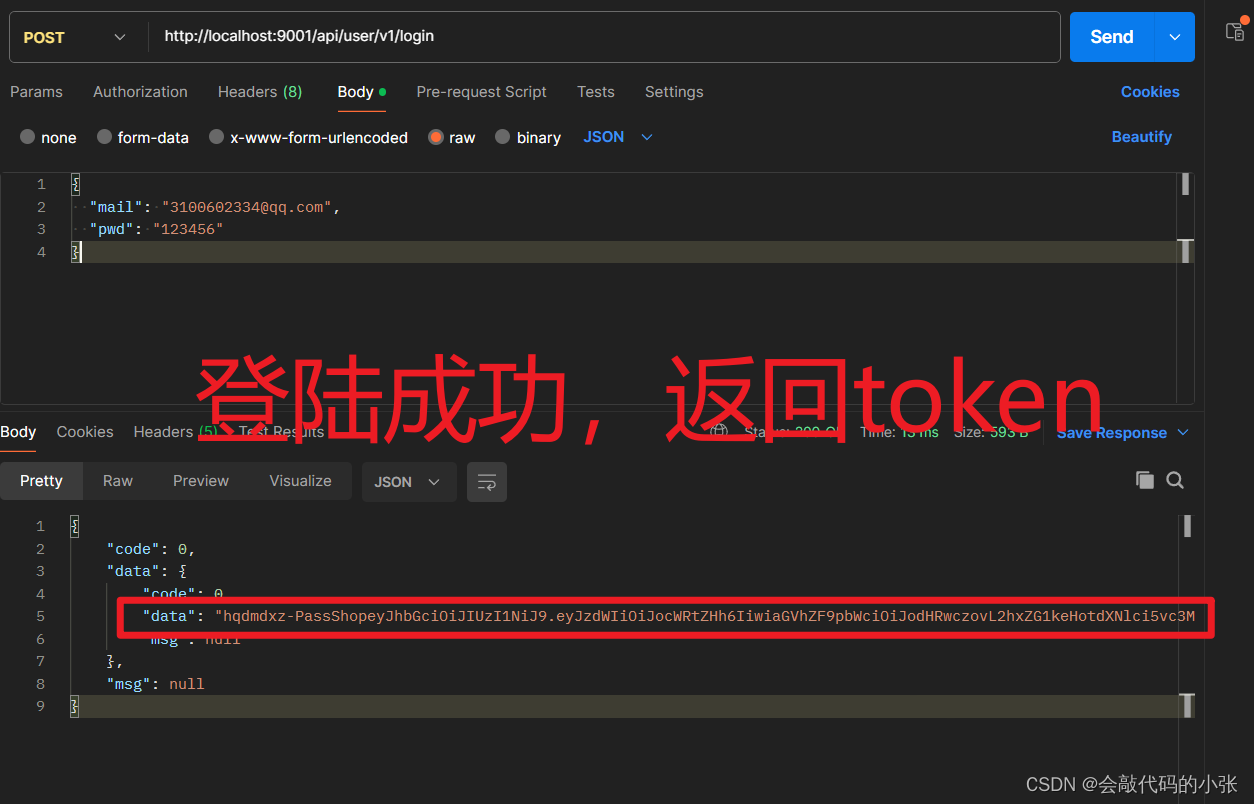
登录校验解决方案JWT
目录 🎗️1.JWT介绍 🎞️2.应用场景 🎟️3.结构组成 🎫4.JWT优点 🎠5.封装成通用方法 🛝6.JWT自动刷新 1.JWT介绍 官网:JWT官网 JSON Web Token (JWT) 是一个开放标准,它…...

Flutter开发进阶之瞧瞧BuildOwner
Flutter开发进阶之瞧瞧BuildOwner 上回说到关于Element Tree的构建还缺最后一块拼图,build的重要过程中会调用_element!.markNeedsBuild();,而markNeedsBuild会调用owner!.scheduleBuildFor(this);。 在Flutter框架中,BuildOwner负责管理构建…...
)
大量免费工具使用(提供api接口)
标题: 免费工具集使用 - 简化你的任务 介绍: 在数字化时代,我们经常需要使用各种工具来完成各种任务。本文将介绍一个免费工具集,它提供了多种实用工具,帮助简化你的任务。这些工具可以在网站 https://tool.kertennet.com 上找到…...
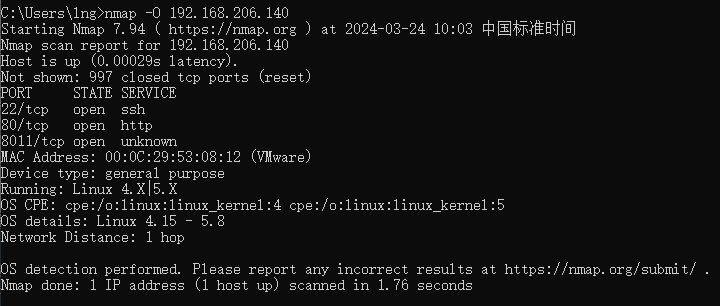
网络探测工具Nmap介绍
1. Nmap简介 Nmap是一款用于网络发现和安全审计的网络安全工具。可用于列举网络主机清单、管理服务升级调度、监控主机、监控主机服务运行状况、检测目标主机是否在线和端口开放情况、侦测运行的服务类型及版本信息、侦测操作系统与设备类型等。 2. 命令大纲 3. 命令详细介绍…...
20240319-2-机器学习基础面试题
⽼板给了你⼀个关于癌症检测的数据集,你构建了⼆分类器然后计算了准确率为 98%, 你是否对这个模型很满意?为什么?如果还不算理想,接下来该怎么做? 首先模型主要是找出患有癌症的患者,模型关注的…...

0202矩阵的运算-矩阵及其运算-线性代数
文章目录 一、矩阵的加法二、数与矩阵相乘三、矩阵与矩阵相乘四、矩阵的转置五、方阵的行列式结语 一、矩阵的加法 定义2 设有两个 m n m\times n mn橘子 A ( a i j ) 和 B ( b i j ) A(a_{ij})和B(b_{ij}) A(aij)和B(bij),那么矩阵A与B的和记为AB,规定为 A B ( a 11…...

python中的__dict__
类的__dict__返回的是:类的静态函数、类函数、普通函数、全局变量以及一些内置的属性都是放在类的__dict__里的, 而实例化对象的:__dict__中存储了一些类中__init__的一些属性值。 import的py文件 __dict__返回的是:__init__的…...

数学分析复习:无穷乘积
文章目录 无穷乘积定义:无穷乘积的收敛性命题:无穷乘积的Cauchy收敛准则正项级数和无穷乘积的联系 本篇文章适合个人复习翻阅,不建议新手入门使用 无穷乘积 设复数列 { a n } n ≥ 1 \{a_n\}_{n\geq 1} {an}n≥1,设对任意 …...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
