Vant Weapp小程序 van-uploader 文件上传点击无反应,删除无反应
Vant Weapp 1.0 版本开始支持van-uploader组件,请先确认好版本号和引用路径正确!!
<van-uploader file-list="{{ fileList }}" deletable="{{ true }}" />
1. 上传无反应
微信小程序用了van-uploader,但是发现点击上传一直没有反应,删除也没反应

最后发现要在微信公众平台配置隐私协议,加上摄像头和照片视频的权限,审核通过后就能用了(好坑)
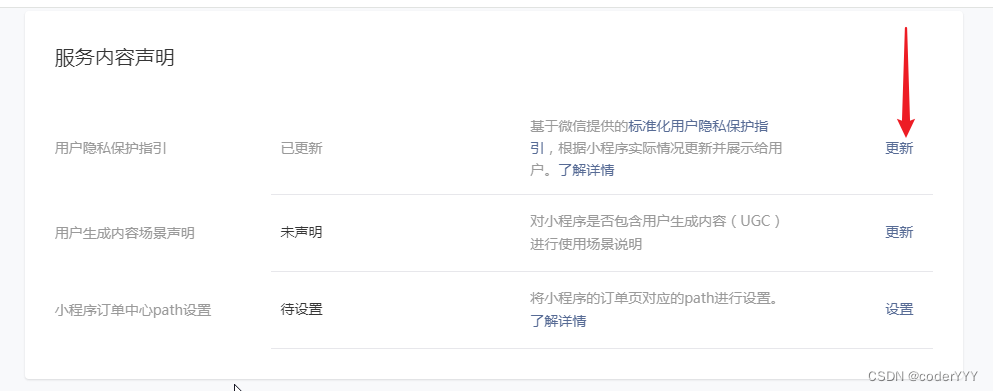
2. 无法删除
点击右上角的叉叉无法删除,没有反应
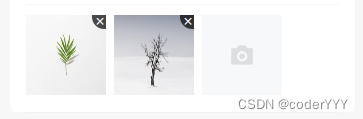
看了组件源码和文档,发现还得监听事件bind:delete才可以

<van-uploader file-list="{{ fileList }}" deletable="{{ true }}" bind:delete="delImg" />
// 删除图片delImg(e) {let index = e.detail.indexconsole.log(index) //图片在fileList的下标let fileList = this.data.fileList;fileList.splice(index, 1);this.setData({fileList})},
相关文章:

Vant Weapp小程序 van-uploader 文件上传点击无反应,删除无反应
Vant Weapp 1.0 版本开始支持van-uploader组件,请先确认好版本号和引用路径正确!! <van-uploader file-list"{{ fileList }}" deletable"{{ true }}" />1. 上传无反应 微信小程序用了van-uploader,但是…...

【力扣】55.跳跃游戏、45.跳跃游戏Ⅱ
55.跳跃游戏 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1&a…...

038—pandas 重采样线性插补
前言 在数据处理时,由于采集数据量有限,或者采集数据粒度过小,经常需要对数据重采样。在本例中,我们将实现一个类型超分辨率的操作。 思路: 首先将原始数据长度扩展为 3 倍,可以使用 loc[] 方法对索引扩…...

智慧工地源码 数字孪生可视化大屏 工地管理平台系统源码 多端展示(PC端、手机端、平板端)
智慧工地源码 数字孪生可视化大屏 工地管理平台系统源码 多端展示(PC端、手机端、平板端) 智慧工地系统多端展示(PC端、手机端、平板端);数字孪生可视化大屏,一张图掌握项目整体情况;使用轻量化模型,部署三…...
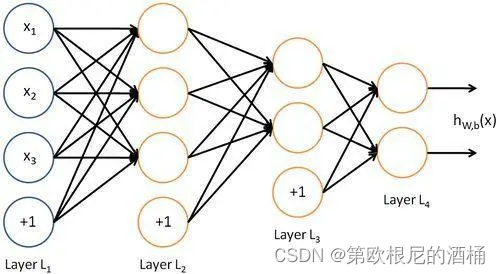
深度学习Top10算法之深度神经网络DNN
深度神经网络(Deep Neural Networks,DNN)是人工神经网络(Artificial Neural Networks,ANN)的一种扩展。它们通过模仿人脑的工作原理来处理数据和创建模式,广泛应用于图像识别、语音识别、自然语…...
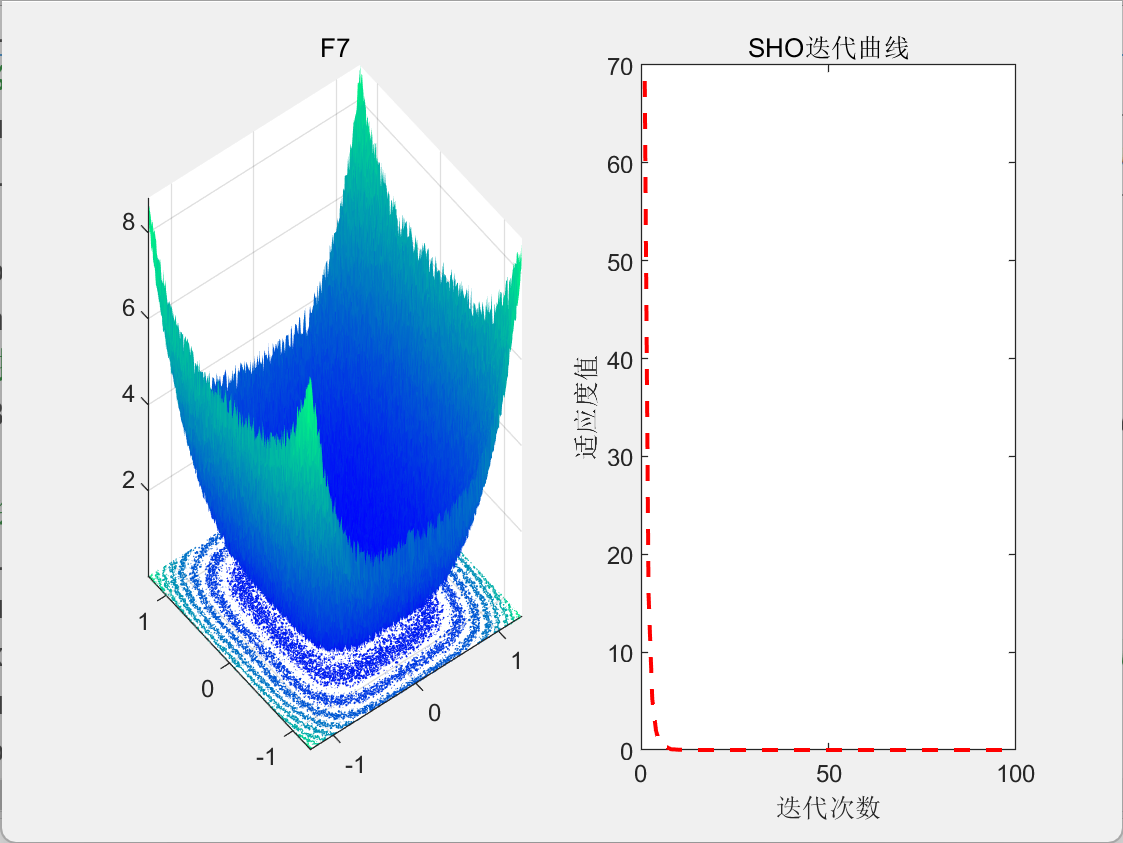
【智能算法】海马优化算法(SHO)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2022年,Zhao等人受到海马自然社会行为启发,提出了海马优化算法(Sea-horse Optimizer, SHO)。 2.算法原理 2.1算法思想 SHO模拟了海马群在自然界中的…...

AI大模型学习的伦理与社会影响
AI大模型学习 随着人工智能技术的快速发展,AI大模型学习成为当前热门研究领域之一。AI大模型学习是指基于大规模数据集和深度学习模型进行训练,以实现更高的准确性和复杂性。这些大模型已经在几乎所有领域都取得了显著的成就,包括自然语言处…...
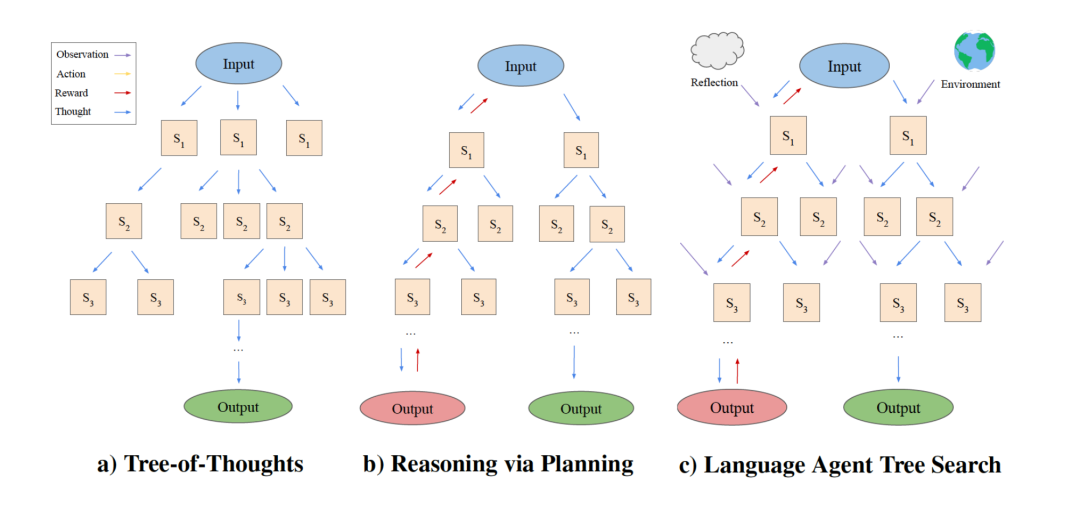
记录些LangChain相关的知识
RAG的输出准确率 RAG的输出准确率 向量信息保留率 * 语义搜索准确率 * LLM准确率RAG的输出准确率由三个因素共同决定:向量信息保留率、语义搜索准确率以及LLM准确率。这三个因素是依次作用的,因此准确率实际上是它们的乘积。这意味着,任何一…...
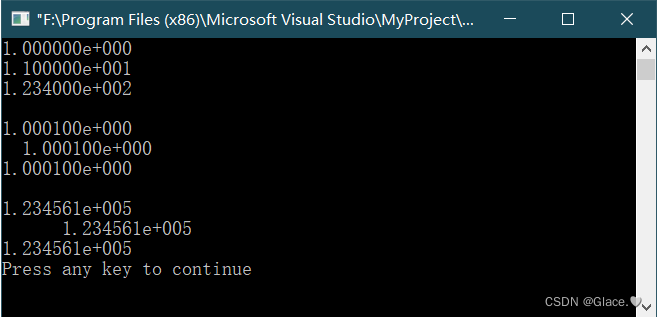
C语言例4-7:格式字符f的使用例子
%f,实型,小数部分为6位 代码如下: //格式字符f的使用例子 #include<stdio.h> int main(void) {float f 123.456;double d1, d2;d11111111111111.111111111;d22222222222222.222222222;printf("%f,%12f,%12.2f,%-12.2f,%.2f\n&qu…...

[蓝桥杯 2019 省 A] 修改数组
题目链接 [蓝桥杯 2019 省 A] 修改数组 题目描述 给定一个长度为 N N N 的数组 A [ A 1 , A 2 , A 3 , . . . , A N ] A [A_1, A_2, A_3, ...,A_N] A[A1,A2,A3,...,AN],数组中有可能有重复出现的整数。 现在小明要按以下方法将其修改为没有重复整数的…...

Git基础(25):Cherry Pick合并指定commit id的提交
文章目录 前言指定commit id合并使用TortoiseGit执行cherry-pick命令 前言 开发中,我们会存在多个分支开发的情况,比如dev,test, prod分支,dev分支在开发新功能,prod作为生产分支已发布。如果某个时候,我们…...

C语言结构体之位段
位段(节约内存),和王者段位联想记忆 位段是为了节约内存的。刚好和结构体相反。 那么什么是位段呢?我们现引入情景:我么如果要记录一个人是男是女,用数字0 1表示。我们发现只要一个bit内存就可以完成我们想…...

2016年认证杯SPSSPRO杯数学建模D题(第二阶段)NBA是否有必要设立四分线全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 D题 NBA是否有必要设立四分线 原题再现: NBA 联盟从 1946 年成立到今天,一路上经历过无数次规则上的变迁。有顺应民意、皆大欢喜的,比如 1973 年在技术统计中增加了抢断和盖帽数据;有应运而生、力…...
登录校验解决方案JWT
目录 🎗️1.JWT介绍 🎞️2.应用场景 🎟️3.结构组成 🎫4.JWT优点 🎠5.封装成通用方法 🛝6.JWT自动刷新 1.JWT介绍 官网:JWT官网 JSON Web Token (JWT) 是一个开放标准,它…...

Flutter开发进阶之瞧瞧BuildOwner
Flutter开发进阶之瞧瞧BuildOwner 上回说到关于Element Tree的构建还缺最后一块拼图,build的重要过程中会调用_element!.markNeedsBuild();,而markNeedsBuild会调用owner!.scheduleBuildFor(this);。 在Flutter框架中,BuildOwner负责管理构建…...
)
大量免费工具使用(提供api接口)
标题: 免费工具集使用 - 简化你的任务 介绍: 在数字化时代,我们经常需要使用各种工具来完成各种任务。本文将介绍一个免费工具集,它提供了多种实用工具,帮助简化你的任务。这些工具可以在网站 https://tool.kertennet.com 上找到…...
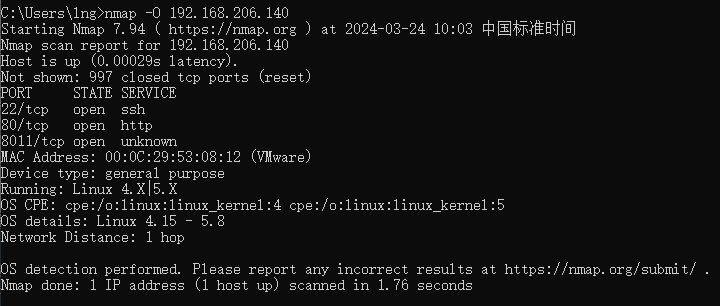
网络探测工具Nmap介绍
1. Nmap简介 Nmap是一款用于网络发现和安全审计的网络安全工具。可用于列举网络主机清单、管理服务升级调度、监控主机、监控主机服务运行状况、检测目标主机是否在线和端口开放情况、侦测运行的服务类型及版本信息、侦测操作系统与设备类型等。 2. 命令大纲 3. 命令详细介绍…...
20240319-2-机器学习基础面试题
⽼板给了你⼀个关于癌症检测的数据集,你构建了⼆分类器然后计算了准确率为 98%, 你是否对这个模型很满意?为什么?如果还不算理想,接下来该怎么做? 首先模型主要是找出患有癌症的患者,模型关注的…...

0202矩阵的运算-矩阵及其运算-线性代数
文章目录 一、矩阵的加法二、数与矩阵相乘三、矩阵与矩阵相乘四、矩阵的转置五、方阵的行列式结语 一、矩阵的加法 定义2 设有两个 m n m\times n mn橘子 A ( a i j ) 和 B ( b i j ) A(a_{ij})和B(b_{ij}) A(aij)和B(bij),那么矩阵A与B的和记为AB,规定为 A B ( a 11…...

python中的__dict__
类的__dict__返回的是:类的静态函数、类函数、普通函数、全局变量以及一些内置的属性都是放在类的__dict__里的, 而实例化对象的:__dict__中存储了一些类中__init__的一些属性值。 import的py文件 __dict__返回的是:__init__的…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
