设计图纸加密方法知多少?小编给你讲清楚

一、对称加密
使用对称加密算法,对设计图纸进行加密。对称加密使用相同的密钥进行加密和解密,确保只有持有正确密钥的人能够解密文件。
二、非对称加密
使用非对称加密算法,进行设计图纸的加密。非对称加密使用公钥加密、私钥解密的方式,可以实现安全的文件传输和加密。
三、哈希加密
使用哈希函数对设计图纸进行加密处理,生成哈希值作为文件的加密形式,用于验证文件的完整性和真实性。
四、文件加密软件
使用文件加密软件对设计图纸进行加密,选择安全的加密算法和设置复杂的密码,确保文件内容的安全性。
图纸加密软件通过采用高强度的加密算法,256位加密,确保图纸文件在存储和传输过程中的安全性,防止数据泄露。同时,软件提供安全的密钥生成、分发和存储机制,保障加密过程的安全性和可靠性。
图纸加密软件允许企业设置不同级别的访问权限,确保只有授权用户才能访问或编辑图纸文件。例如,软件支持基于角色的权限管理,可以精确控制每个用户的访问权限,从而增强数据安全性。
图纸加密软件能够对图纸的访问和修改进行详细记录,便于事后审计和追踪。日志包括访问时间、用户身份、操作类型等信息,有助于企业监控数据使用情况并及时发现潜在的安全威胁。
图纸加密软件能够与企业现有的IT系统和其他应用程序无缝集成,简化部署和管理过程。例如,软件支持与云存储服务集成,方便用户在不同设备间同步和共享加密图纸。

五、加密压缩
将设计图纸先进行压缩处理,然后再进行加密,可以减小文件大小并增加安全性。
六、密码保护
对设计图纸设置密码保护,只有知道密码的人才能够打开和查看文件内容。
七、数字签名
使用数字签名技术对设计图纸进行签名,确保文件的完整性和真实性,防止文件被篡改。
八、水印技术
在设计图纸中添加水印,用于标识文件的所有权和保护文件内容不被盗用。
相关文章:

设计图纸加密方法知多少?小编给你讲清楚
一、对称加密 使用对称加密算法,对设计图纸进行加密。对称加密使用相同的密钥进行加密和解密,确保只有持有正确密钥的人能够解密文件。 二、非对称加密 使用非对称加密算法,进行设计图纸的加密。非对称加密使用公钥加密、私钥解密的方式&a…...

pycv实时目标检测快速实现
使用python_cv实现目标实时检测 python 安装依赖核心代码快速使用实现结果展示enjoy python 安装依赖 opencv_python4.7.0.72 pandas1.5.3 tensorflow2.11.0 tensorflow_hub0.13.0 tensorflow_intel2.11.0 numpy1.23.5核心代码快速使用 # 使用了TensorFlow Hub和OpenCV库来实…...

记录下如何让字体在div内 自动换行 上下居中
div内样式 display: flex; // flex布局 justify-content: center; // 上下居中 align-items: center; // 左右居中 overflow-wrap: break-word; // 允许字体换行 (若行内的单词无法放下则换行) word-break: break-all; // 强制文本在任意字符间进…...

Shell篇之编写MySQL启动脚本
Shell篇之编写MySQL启动脚本 1. 脚本内容 vim mysql_ctl.sh#!/bin/bashmysql_port3306 mysql_username"root" mysql_password"molinker" mysql_conf"/opt/lanmp/mysql/etc/my.cnf" mysql_sock"/opt/lanmp/mysql/var/mysql.sock"func…...

supermap Iclient3d for cesium加载地形并夸大地形
先看效果图 这是没有夸张之前的都江堰 这是夸大五倍后的都江堰 下面展示代码 主要就是加载supermaponline的skt地形然后夸大 <template><div class"PartOneBox"><div id"cesiumContainer"></div></div> </template>…...

一文解读OLAP的工具和应用软件
OLAP(OnlineAnalyticalProcessing)是一种用于快速分析大规模、多维度数据的方法。OLAP工具和应用软件则是帮助人们进行OLAP分析的重要工具。本文将介绍几种常见的OLAP工具和应用软件,并探讨它们在数据分析中的作用。 一 OLAP工具的分类 在选…...
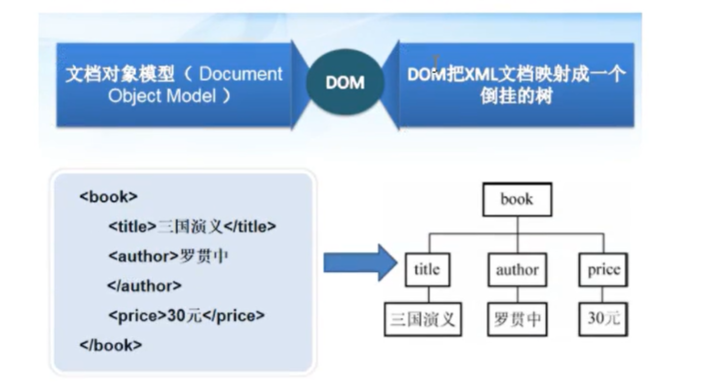
xml重点笔记(尚学堂 3h)
XML:可扩展标记语言 主要内容(了解即可) 1.XML介绍 2.DTD 3.XSD 4.DOM解析 6.SAX解析 学习目标 一. XML介绍 1.简介 XML(Extensible Markup Language) 可扩展标记语言,严格区分大小写 2.XML和HTML XML是用来传输和存储数据的。 XML多用在框架的配置文件…...
爬虫代理API的全面解析:让数据抓取更高效
在大数据时代,网络爬虫已经成为收集和分析数据的重要工具。然而,频繁的请求会导致IP被封禁,这时候爬虫代理API就显得尤为重要。本文将详细介绍爬虫代理API的作用、优势及如何使用,帮助你更高效地进行数据抓取。 什么是爬虫代理AP…...

PCL 点云中的植被信息提取(C++详细过程版)
目录 一、算法原理1、原理概述2、参考文献二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接,首发于:2024年9月18日。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的抄袭狗。 一、算法原理 1、原理概述 点云具有丰富的色彩信息,可以与植被指数结合使…...

requests-html的具体使用方法有哪些?
requests-html是一个功能强大的Python库,用于发送HTTP请求和解析HTML内容。它的使用方法包括安装库、基本使用、发送带有参数的请求、图片抓取实战案例、解析网页内容、执行JavaScript代码、使用CSS选择器来查找元素、继续跟踪链接并获取内容等。 安装request…...

YOLOv9改进策略【卷积层】| AKConv: 具有任意采样形状和任意参数数量的卷积核
一、本文介绍 本文记录的是利用AKConv优化YOLOv9的目标检测网络模型。标准卷积操作的卷积运算局限于局部窗口,无法捕获其他位置的信息,且采样形状固定,无法适应不同数据集和位置中目标形状的变化。而AKConv旨在为卷积核提供任意数量的参数和…...

图神经网络池化方法
图神经网络池化方法 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 图神经网络池化方法前言一、扁平图池化二、分层图池化1.节点聚类池化2.节点丢弃池化 参考文献 前言 图池化操作根据其池化策略的差异ÿ…...

小琳AI课堂:确保大语言模型安全的八大策略--从数据隐私到用户教育
大家好,这里是小琳AI课堂。今天我们深入探讨如何保证大语言模型的安全,这可是关系到我们每个人哦!🔐 首先,我们要明白,保证大语言模型的安全,需要从多个方面入手,确保模型在技术、法…...

Python 数学建模——高斯核密度估计
文章目录 前言原理代码实例scipy 实现seaborn 实现 前言 高斯核密度估计本是一种机器学习算法,在数学建模中也可以发挥作用。本文主要讨论用它来拟合变量的概率密度,获得概率密度函数 f ( x ) f(x) f(x)。 原理 已知一个连续型随机变量 X X X 的一系列…...

Flink+Spark相关记录
FlinkSpark相关记录 FlinkSQL Flink Streaming的一些点覆写RichSource、RichSink、RichMap 1.Source自动负载均衡,CDC源端加入一个全局调控的节点监控流量流速 2.Sink并发写入 3.Map与Iterator与增量迭代等用法关于Checkpoint几个用法 1.提交Commit至目的端数据库 2…...

2023 hnust 湖科大 毕业实习 报告+实习鉴定表
2023 hnust 湖科大 毕业实习 报告实习鉴定表 岗位 IT公司机房运维 实习报告 实习鉴定表 常见疑问 hnust 湖科大 毕业实习常见问题30问(2021 年7月,V0.9)-CSDN博客时间:大四开学第三四周毕业实习23年是企业(黑马&am…...

ConflictingBeanDefinitionException | 运行SpringBoot项目时报错bean定义冲突解决方案
具体报错: Caused by: org.springframework.context.annotation.ConflictingBeanDefinitionException: Annotation-specified bean name ‘CommissionMapperImpl’ for bean class [com.xxx.mapper.carrier.CommissionMapperImpl] conflicts with existing, non-co…...
【2024版】)
如何切换淘宝最新镜像源(npm)【2024版】
在使用 Node.js 和 npm 进行开发时,大家通常会遇到 npm 源速度较慢的问题。特别是当你需要安装大量依赖时,npm 官方源的速度可能不尽如人意。幸运的是,淘宝提供了一个更快速的 npm 镜像源,可以让你更快地下载和安装包。本文将介绍…...
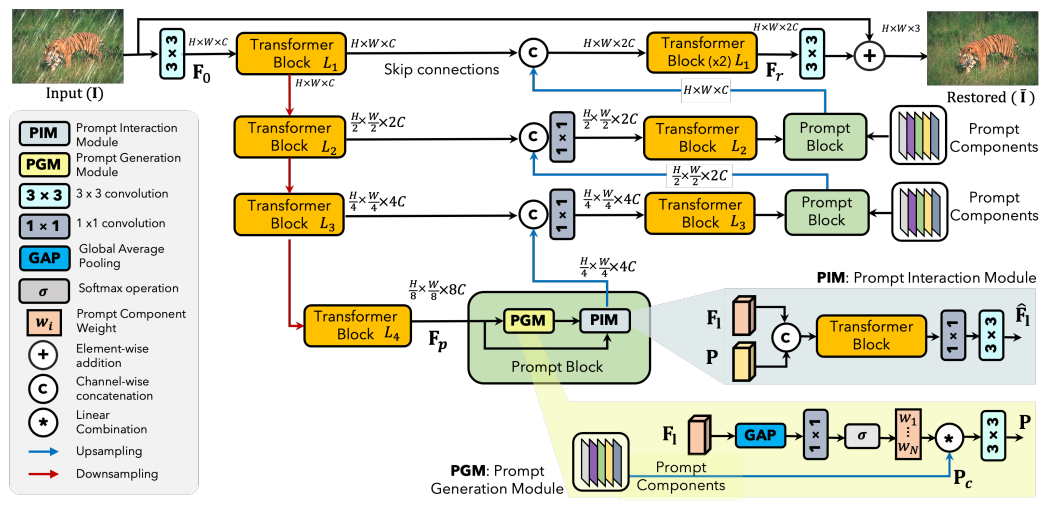
YoloV10改进策略:Block改进|PromptIR(NIPS‘2023)|轻量高效,即插即用|(适用于分类、分割、检测等多种场景)
文章目录 摘要代码详解如何在自己的论文中描述改进方法测试结果总结摘要 本文使用PromptIR框架中的PGM模块来改进YoloV10。PGM(Prompt Generation Module)模块是PromptIR框架中的一个重要组成部分,主要负责生成输入条件化的提示(prompts)。这些提示是一组可学习的参数,它…...

使用rust自制操作系统内核
一、系统简介 本操作系统是一个使用rust语言实现,基于32位的x86CPU的分时操作系统。 项目地址(求star):GitHub - CaoGaorong/os-in-rust: 使用rust实现一个操作系统内核 详细文档:自制操作系统 语雀 1. 项目特性 …...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
