《Effects of Graph Convolutions in Multi-layer Networks》阅读笔记
一.文章概述
本文研究了在XOR-CSBM数据模型的多层网络的第一层以上时,图卷积能力的基本极限,并为它们在数据中信号的不同状态下的性能提供了理论保证。在合成数据和真实世界数据上的实验表明a.卷积的数量是决定网络性能的一个更重要的因素,而不是网络中的层的数量。b.只要放置相同数量的卷积层,只要不在第一层,任何放置组合能实现相似的性能增强。c.当图相对稀疏的时候,多个图卷积是有利的。
注意,本文研究的重点是比较图卷积与不利用关系信息的传统MLP的优点和局限性。作者的设置不受异配性问题的影响,且不考虑过平滑发生的情况。
二.预备知识
数据模型
令 n n n表示数据点的数量, d d d表示特征维度。定义伯努利随机变量 ε 1 , … , ε n ∼ Ber ( 1 / 2 ) \varepsilon_1, \ldots, \varepsilon_n \sim \operatorname{Ber}(1 / 2) ε1,…,εn∼Ber(1/2)和 η 1 , … , η n ∼ Ber ( 1 / 2 ) \eta_1, \ldots, \eta_n \sim \operatorname{Ber}(1 / 2) η1,…,ηn∼Ber(1/2)。定义两个类别 C b = { i ∈ [ n ] ∣ ε i = b } C_b=\left\{i \in[n] \mid \varepsilon_i=b\right\} Cb={i∈[n]∣εi=b},其中 b ∈ { 0 , 1 } b \in\{0,1\} b∈{0,1}。
令 μ \boldsymbol{\mu} μ和 ν \boldsymbol{\nu} ν表示 R d \mathbb{R}^d Rd中的固定向量,其满足 ∥ μ ∥ 2 = ∥ ν ∥ 2 \|\boldsymbol{\mu}\|_2=\|\boldsymbol{\nu}\|_2 ∥μ∥2=∥ν∥2 和 ⟨ μ , ν ⟩ = 0 \langle\boldsymbol{\mu}, \boldsymbol{\nu}\rangle=0 ⟨μ,ν⟩=0(即 μ \boldsymbol{\mu} μ和 ν \boldsymbol{\nu} ν正交)。令 X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d为数据矩阵,其中每行 X i ∈ R d \mathbf{X}_i \in \mathbb{R}^d Xi∈Rd是一个独立的高斯随机向量分布 X i ∼ N ( ( 2 η i − 1 ) ( ( 1 − ε i ) μ + ε i ν ) , σ 2 ) \mathbf{X}_i \sim \mathcal{N}\left(\left(2 \eta_i-1\right)\left(\left(1-\varepsilon_i\right) \boldsymbol{\mu}+\varepsilon_i \boldsymbol{\nu}\right), \sigma^2\right) Xi∼N((2ηi−1)((1−εi)μ+εiν),σ2)。用 X ∼ XOR − GMM ( n , d , μ , ν , σ 2 ) \mathbf{X} \sim \operatorname{XOR}-\operatorname{GMM}\left(n, d, \boldsymbol{\mu}, \boldsymbol{\nu}, \sigma^2\right) X∼XOR−GMM(n,d,μ,ν,σ2)表示从该数据模型中采样的数据。
令 A = ( a i j ) i , j ∈ [ n ] \mathbf{A}=\left(a_{i j}\right)_{i, j \in[n]} A=(aij)i,j∈[n]表示对应于图(含自环的无向图)信息的邻接矩阵,该矩阵是从一个标准的对称双块随机块模型(symmetric two-block stochastic block model)中采样的,该模块的参数为 p p p和 q q q,其中 p p p表示块内边概率, q q q表示块间边概率。作者将 SBM ( n , p , q ) \operatorname{SBM}(n, p, q) SBM(n,p,q)与 XOR − GMM ( n , d , μ , ν , σ 2 ) \operatorname{XOR}-\operatorname{GMM}\left(n, d, \boldsymbol{\mu}, \boldsymbol{\nu}, \sigma^2\right) XOR−GMM(n,d,μ,ν,σ2)耦合在一起,即若 ε i = ε j \varepsilon_i=\varepsilon_j εi=εj,则 a i j ∼ Ber ( p ) a_{i j} \sim \operatorname{Ber}(p) aij∼Ber(p),否则 a i j ∼ Ber ( q ) a_{i j} \sim \operatorname{Ber}(q) aij∼Ber(q)。
至此,可得定义的数据模型 ( A , X ) = ( { a i j } i , j ∈ [ n ] , { X i } i ∈ [ n ] ) (\mathbf{A}, \mathbf{X})=\left(\left\{a_{i j}\right\}_{i, j \in[n]},\left\{\mathbf{X}_i\right\}_{i \in[n]}\right) (A,X)=({aij}i,j∈[n],{Xi}i∈[n]),即 ( A , X ) ∼ XOR − CSBM ( n , d , μ , ν , σ 2 , p , q ) (\mathbf{A}, \mathbf{X}) \sim \operatorname{XOR}-\operatorname{CSBM}\left(n, d, \boldsymbol{\mu}, \boldsymbol{\nu}, \sigma^2, p, q\right) (A,X)∼XOR−CSBM(n,d,μ,ν,σ2,p,q)。
令 D \mathbf{D} D表示邻接矩阵对应的度矩阵, N i = { j ∈ [ n ] ∣ a i j = 1 } N_i=\left\{j \in[n] \mid a_{i j}=1\right\} Ni={j∈[n]∣aij=1}表示节点 i i i的邻居集。
网络架构
作者的分析聚焦于带ReLU激活的MLP架构, L L L层网络定义如下:
H ( 0 ) = X f ( l ) ( X ) = ( D − 1 A ) k l H ( l − 1 ) W ( l ) + b ( l ) H ( l ) = ReLU ( f ( l ) ( X ) ) y ^ = φ ( f ( L ) ( X ) ) . \begin{aligned} & \mathbf{H}^{(0)}=\mathbf{X} \\ & f^{(l)}(\mathbf{X})=\left(\mathbf{D}^{-1} \mathbf{A}\right)^{k_l} \mathbf{H}^{(l-1)} \mathbf{W}^{(l)}+\mathbf{b}^{(l)} \\ & \mathbf{H}^{(l)}=\operatorname{ReLU}\left(f^{(l)}(\mathbf{X})\right) \\ & \hat{\mathbf{y}}=\varphi\left(f^{(L)}(\mathbf{X})\right) . \end{aligned} H(0)=Xf(l)(X)=(D−1A)klH(l−1)W(l)+b(l)H(l)=ReLU(f(l)(X))y^=φ(f(L)(X)).
其中 l ∈ [ L ] l \in [L] l∈[L], φ ( x ) = sigmoid ( x ) = \varphi(x)=\operatorname{sigmoid}(x)= φ(x)=sigmoid(x)= 1 1 + e − x \frac{1}{1+e^{-x}} 1+e−x1,最后一层的输出表示为 y ^ = { y ^ i } i ∈ [ n ] \hat{\mathbf{y}}=\left\{\hat{y}_i\right\}_{i \in[n]} y^={y^i}i∈[n]。 D − 1 A \mathbf{D}^{-1} \mathbf{A} D−1A表示正则化的邻接矩阵, k l k_l kl表示层 l l l中的图卷积数量。对于给定数据集 ( X , y ) (\mathbf{X}, \mathbf{y}) (X,y),采用二进制交叉熵来进行优化:
ℓ θ ( A , X ) = − 1 n ∑ i ∈ [ n ] y i log ( y ^ i ) + ( 1 − y i ) log ( 1 − y ^ i ) \ell_\theta(\mathbf{A}, \mathbf{X})=-\frac{1}{n} \sum_{i \in[n]} y_i \log \left(\hat{y}_i\right)+\left(1-y_i\right) \log \left(1-\hat{y}_i\right) ℓθ(A,X)=−n1i∈[n]∑yilog(y^i)+(1−yi)log(1−y^i)
三.理论分析结果
设置Baselines
作者设置了一个没有图信息的对比baseline。作者用用混合模型的均值与数据点数 n n n之间的距离来表征XOR-GMM数据模型的分类阈值。令 Φ ( ⋅ ) \Phi(\cdot) Φ(⋅) 表示标准高斯的累积分布函数。
重要结论:若两个类的特征均值相距不超过 O ( σ ) O(\sigma) O(σ),那么在压倒性的概率下,有常数比例的点被错误分类。
通过图卷积进行改进
本节阐述了图卷积在多层卷积中的影响。
重要结论:多层模型中将图卷积放置在第一层会损害分类精度,下图(a)展示的的便是第一层中没有图卷积的网络,可见不同类别的数据并不是线性可分的,对其进行图卷积后,两个类的均值会坍缩到同一点,如图(b)。然后,在最后一层使用图卷积则不同,由于输入由线性可分的转换特征组成,图卷积有助于分类任务。

图卷积的放置
多层网络分类能力的提高取决于卷积的数量,而不取决于卷积放置的位置。对于XOR-CSBM数据模型,在任何组合中在第二层和/或第三层之间放置相同数量的卷积,可以在分类任务中实现与上节相似的改进。
四.实验
本节通过实验证明第四节中的结论。
合成数据集
图卷积的位置并不重要,只要它不在第一层,(a)和(b)表明对于在第二层或第三层中有一个图卷积的所有网络,以及在第二层和第三层之间的任何组合中有两个图卷积的所有网络,性能是相互相似的。
在图是dense的情况下,两个图卷积并不比一个图卷积获得显著的优势。(参见图©和图(d))

真实世界数据集
作者在论文引用网络Cora、Citeseer和Pubmed上进行实验,得到结论为:
- 利用图的网络比不使用关系信息的传统MLP表现得明显更好。
- 在任何层中具有一个图卷积的所有网络都实现了相互相似的性能,并且在任何位置组合中具有两个图卷积的所有网络都实现了相互相似的性能。

相关文章:

《Effects of Graph Convolutions in Multi-layer Networks》阅读笔记
一.文章概述 本文研究了在XOR-CSBM数据模型的多层网络的第一层以上时,图卷积能力的基本极限,并为它们在数据中信号的不同状态下的性能提供了理论保证。在合成数据和真实世界数据上的实验表明a.卷积的数量是决定网络性能的一个更重要的因素,而…...

低代码助力传统制造业数字化转型策略
随着制造强国战略逐步实施,制造行业数字化逐渐进入快车道。提高生产管理的敏捷性、加强产品的全生命周期质量管理是企业数字化转型的核心诉求,也是需要思考的核心价值。就当下传统制造业的核心问题来看,低代码是最佳解决方案,那为…...

什么叫做云计算
什么叫做云计算 相信大多数人对云计算或者是云服务的认识还停留在仅仅听过这个名词,但是对其真正的定义或者意义还不甚了解的层面。甚至有些技术人员,如果日常的业务不涉及到云服务,可能对其也只是一知半解的程度。首先云计算准确的讲只是云服…...

springboot 使用zookeeper实现分布式队列
一.添加ZooKeeper依赖:在pom.xml文件中添加ZooKeeper客户端的依赖项。例如,可以使用Apache Curator作为ZooKeeper客户端库: <dependency><groupId>org.apache.curator</groupId><artifactId>curator-framework</…...
地理数据的双重呈现:GIS与数据可视化
前一篇文章带大家了解了GIS与三维GIS的关系,本文就GIS话题带大家一起探讨一下GIS和数据可视化之间的关系。 GIS(地理信息系统)和数据可视化在地理信息科学领域扮演着重要的角色,它们之间密切相关且相互增强。GIS是一种用于采集、…...
- MediaPlayer生命周期)
Android 13 Media框架(3)- MediaPlayer生命周期
上一节了解了MediaPlayer api的使用,这一节就我们将会了解MediaPlayer的生命周期与api使用细节。 1、MediaPlayer生命周期 MediaPlayer.java 一开始有对生命周期的描述,这里对这些内容进行翻译: MediaPlayer 是线程不安全的,创建…...
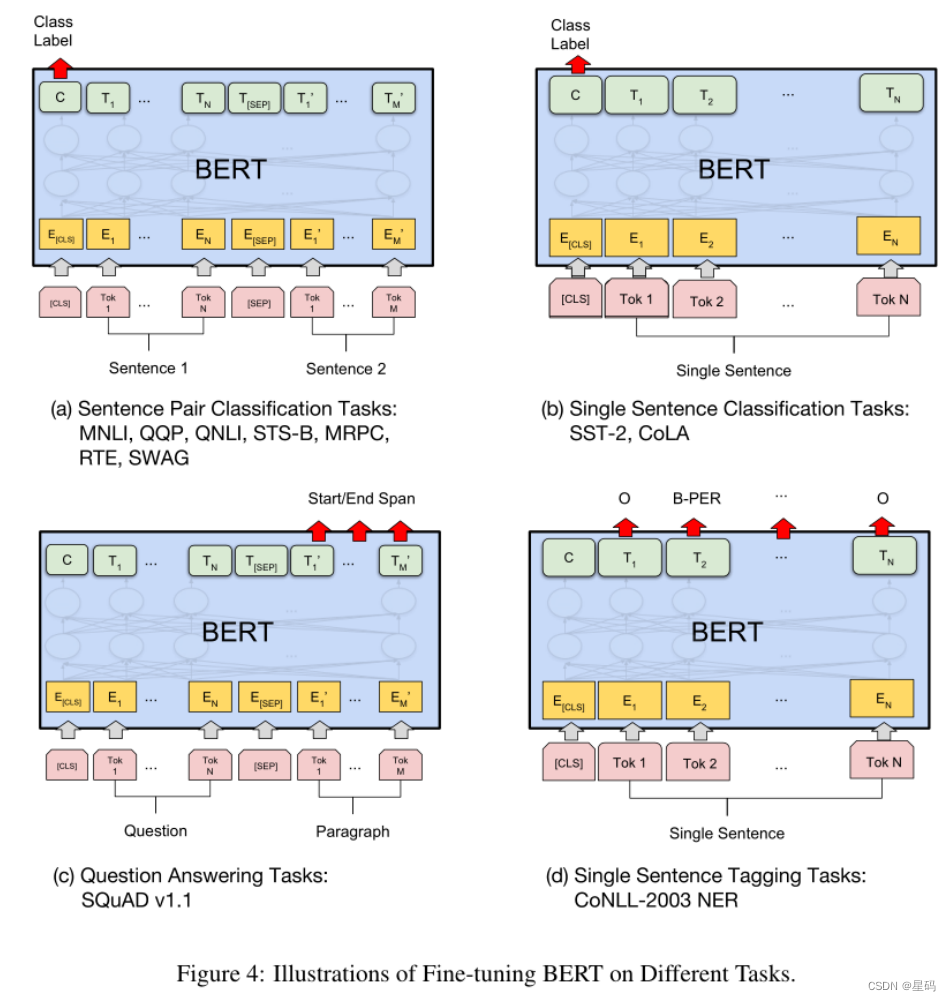
[oneAPI] BERT
[oneAPI] BERT BERT训练过程Masked Language Model(MLM)Next Sentence Prediction(NSP)微调 总结基于oneAPI代码 比赛:https://marketing.csdn.net/p/f3e44fbfe46c465f4d9d6c23e38e0517 Intel DevCloud for oneAPI&…...

F1-score解析
报错:valueError: Target is multiclass but average‘binary’. Please choose another average setting, one of 原因:使用from sklearn.metrics import f1_score多类别计算F1-score时报错,改函数的参数即可,如:f1_s…...
windows11下配置vscode中c/c++环境
本文默认已经下载且安装好vscode,主要是解决环境变量配置以及编译task、launch文件的问题。 自己尝试过许多博客,最后还是通过这种方法配置成功了。 Linux(ubuntu 20.04)配置vscode可以直接跳转到配置task、launch文件,不需要下载mingw与配…...

Max Sum
一、题目 Given a sequence a[1],a[2],a[3]…a[n], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 (-1) 5 4 14. Input The first line of the input contains an integer T(1<T<…...
Field injection is not recommended
文章目录 1. 引言2. 不推荐使用Autowired的原因3. Spring提供了三种主要的依赖注入方式3.1. 构造函数注入(Constructor Injection)3.2. Setter方法注入(Setter Injection)3.3. 字段注入(Field Injection) 4…...
C#字符串占位符替换
using System;namespace myprog {class test{static void Main(string[] args){string str1 string.Format("{0}今年{1}岁,身高{2}cm,月收入{3}元;", "小李", 23, 177, 5000);Console.WriteLine(str1);Console.ReadKey(…...
ChatGPT等人工智能编写文章的内容今后将成为常态
BuzzFeed股价上涨200%可能标志着“转向人工智能”媒体趋势的开始。 周四,一份内部备忘录被华尔街日报透露BuzzFeed正计划使用ChatGPT聊天机器人-风格文本合成技术来自OpenAI,用于创建个性化盘问和将来可能的其他内容。消息传出后,BuzzFeed的…...
)
【Sklearn】基于梯度提升树算法的数据分类预测(Excel可直接替换数据)
【Sklearn】基于梯度提升树算法的数据分类预测(Excel可直接替换数据) 1.模型原理2.模型参数3.文件结构4.Excel数据5.下载地址6.完整代码7.运行结果1.模型原理 梯度提升树(Gradient Boosting Trees)是一种集成学习方法,用于解决分类和回归问题。它通过将多个弱学习器(通常…...

什么叫做云计算?
相信大多数人对云计算或者是云服务的认识还停留在仅仅听过这个名词,但是对其真正的定义或者意义还不甚了解的层面。甚至有些技术人员,如果日常的业务不涉及到云服务,可能对其也只是一知半解的程度。首先云计算准确的讲只是云服务中的一部分&a…...

深度学习Batch Normalization
批标准化(Batch Normalization,简称BN)是一种用于深度神经网络的技术,它的主要目的是解决深度学习模型训练过程中的内部协变量偏移问题。简单来说,当我们在训练深度神经网络时,每一层的输入分布都可能会随着…...

el-table实现懒加载(el-table-infinite-scroll)
2023.8.15今天我学习了用el-table对大量的数据进行懒加载。 效果如下: 1.首先安装: npm install --save el-table-infinite-scroll2 2.全局引入: import ElTableInfiniteScroll from "el-table-infinite-scroll";// 懒加载 V…...

vueRouter回顾
关于vueRouter的两种路由模式 “history” 模式使用正常的 URL 格式,例如 https://example.com/path。“hash” 模式将路由信息添加到 URL 的哈希部分(#)后面,例如 https://example.com/#/path。 1、history模式:没有…...

大规模无人机集群算法flocking(蜂群)
matlab2016b正常运行...
【第三阶段】kotlin语言的split
const val INFO"kotlin,java,c,c#" fun main() {//list自动类型推断成listList<String>val listINFO.split(",")//直接输出list集合,不解构println("直接输出list的集合元素:$list")//类比c有解构,ktoli…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
