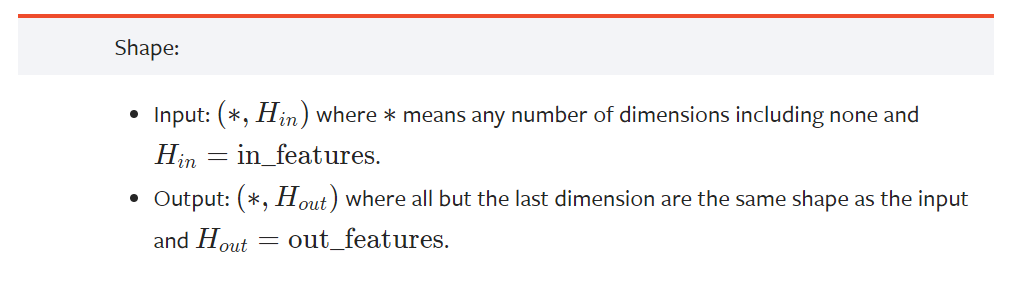
HyperOpt-quniform 范围问题
在使用 quniform 的时候,可能会出现超出指定范围的值,例如对于 GBDT 设置参数空间为 'learning_rate':hp.quniform('learning_rate',0.05,2.05,0.2),但是仍然会报错 ValueError: learning_rate must be greater than 0 but was 0.0,但我们并没有把 0 设置在范围内。
实际上,Hyperopt 对于 quniform 的处理并不是类似于 range(起始,终止,步长) ,而是另一种处理方式,这里可以查看官方文档
hp.quniform(label, low, high, q)
Returns a value like round (uniform (low, high) / q) * q
返回像 round (uniform (low, high) / q) * q 的值
Suitable for a discrete value with respect to which the objective is still somewhat “smooth”, but which should be bounded both above and below.
适用于相对取值仍然有点“平滑”,但应有上下限限制的离散值。
进一步,我们需要看一下 uniform 的定义
hp.uniform(label, low, high)
Returns a value uniformly between low and high.
返回值介于在 low 和 hight 之间
When optimizing, this variable is constrained to a two-sided interval.
在优化的时候,这个变量被限制在最大值和最小值中间
因此对于上面的报错我们就可以找到原因了。根据给出的公式
round(uniform(low,high)/q)∗qround (uniform (low, high) / q) * qround(uniform(low,high)/q)∗q
,我们代入任意小于 12q\frac{1}{2}q21q 的的值,该式即为
round(12q−ϵq)∗q=round(1/2−ϵ)∗q=0∗q=0\begin{aligned} &round(\frac{\frac{1}{2}q-\epsilon }{q})*q\\ =&round(1/2-\epsilon )*q\\ =&0*q\\ =&0 \end{aligned} ===round(q21q−ϵ)∗qround(1/2−ϵ)∗q0∗q0
这里 ϵ\epsilonϵ 是一个很小的正数。
相关文章:

HyperOpt-quniform 范围问题
在使用 quniform 的时候,可能会出现超出指定范围的值,例如对于 GBDT 设置参数空间为 learning_rate:hp.quniform(learning_rate,0.05,2.05,0.2),但是仍然会报错 ValueError: learning_rate must be greater than 0 but was 0.0,但…...

Pycharm搭建一个Django项目
File->new project 点击create, 等待一下即可 查看安装 Django 版本: 在 Pycharm 底部选择 Terminal 然后在里面输入:python -m django --version 启动项目: 在 Terminal 里面输入: python manage.py runserver 查看文件目…...

浅析前端工程化中的一部曲——模块化
在日益复杂和多元的 Web 业务背景下,前端工程化经常会被提及。工程化的目的是高性能、稳定性、可用性、可维护性、高效协同,只要是以这几个角度为目标所做的操作,都可成为工程化的一部分。工程化是软件工程中的一种思想,当下的工程…...

新版bing(集成ChatGPT)申请通过后在谷歌浏览器(Chrome)上的使用方法
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,科大讯飞比赛第三名,CCF比赛第四名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…...
Time-distributed 的理解
前言 今天看到论文中用到 Time-distributed CNN,第一次见到 Time-distributed,不理解是什么含义,看到代码实现也很懵。不管什么网络结构,外面都能套一个TimeDistributed。看了几个博客,还是不明白,问了问C…...

matlab 计算矩阵的Moore-Penrose 伪逆
目录 一、Moore-Penrose 伪逆1、主要函数2、输入输出参数二、代码示例使用伪逆求解线性方程组一、Moore-Penrose 伪逆 Moore-Penrose 伪逆是一种矩阵,可在不存在逆矩阵的情况下作为逆矩阵的部分替代。此矩阵常被用于求解没有唯一解或有许多解的线性方程组。 对于任何矩阵…...

简历制作方面的经验与建议
专栏推荐:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 专栏首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 专栏内容: 笔试复盘篇 2023秋招过程中整理的笔试题,来源包括我自己求职笔试以及整理其他同学的笔试。包含华为、中兴、联发科、AMD、大…...

C语言--static、const、volatile关键字
Static static修饰局部变量改变了变量的生命周期,让静态局部变量出了作用域依然存在,到程序结束,生命周期才结束。 static 修饰局部变量 改变局部变量的生命周期,本质上是改变了局部变量的存储位置,让局部变量不再是…...

Rust学习入门--【18】Rust结构体
系列文章目录 Rust 语言是一种高效、可靠的通用高级语言,效率可以媲美 C / C 。本系列文件记录博主自学Rust的过程。欢迎大家一同学习。 Rust学习入门–【1】引言 Rust学习入门–【2】Rust 开发环境配置 Rust学习入门–【3】Cargo介绍 Rust学习入门–【4】Rust 输…...
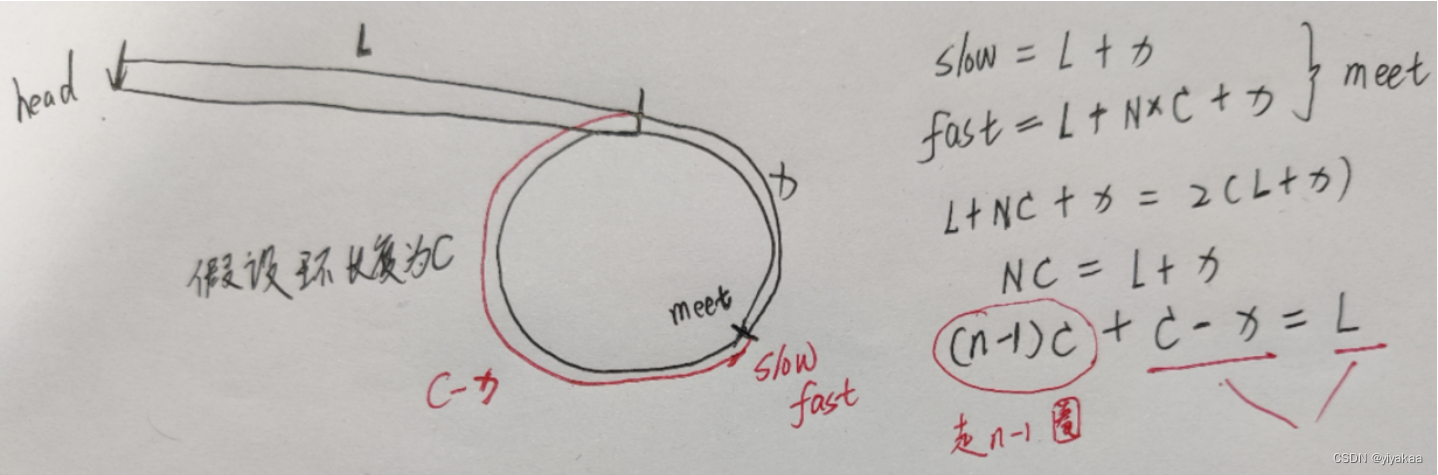
LeetCode142 环形链表Ⅱ
题目: 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评…...

JavaScript刷LeetCode拿offer-高频链表题
首先需要了解链表的概念 先把 next 记录下来 无论是插入,删除,还是翻转等等操作,先把 next 指针用临时变量保存起来,这可以解决 90% 重组链表中指向出错的问题, 如果不知道什么时候需要用到守卫,那就都用…...
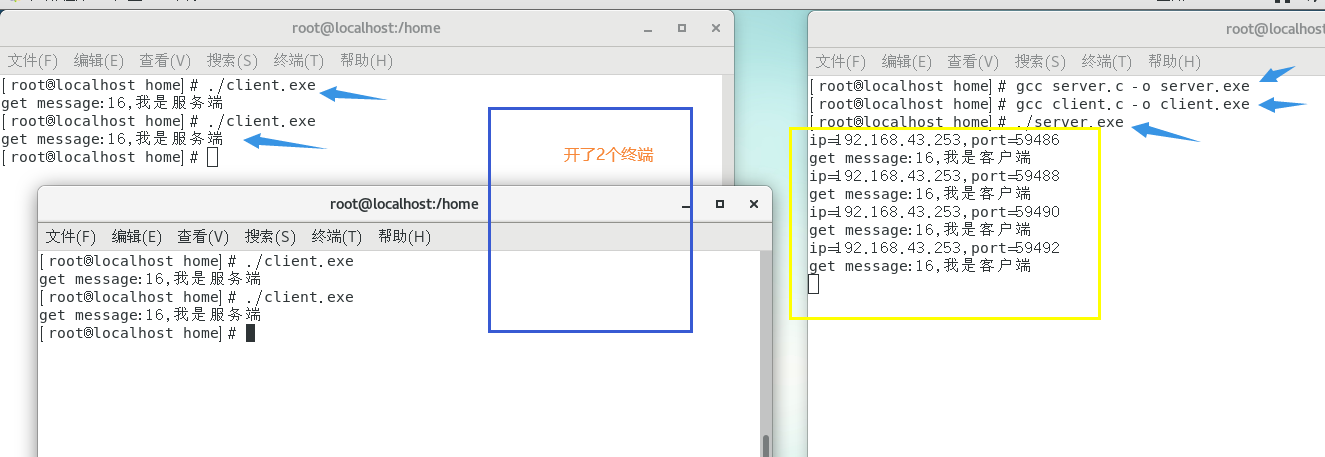
linux系统编程2--网络编程
在linux系统编程中网络编程是使用socket(套接字),socket这个词可以表示很多概念:在TCP/IP协议中,“IP地址TCP或UDP端口号”唯一标识网络通讯中的一个进程,“IP地址端口号”就称为socket。在TCP协议中&#…...
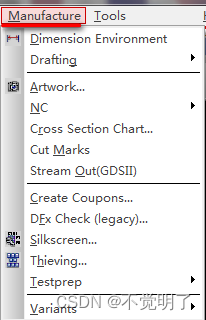
Allegro如何重命名光绘操作指导
Allegro如何重命名光绘操作指导 在做PCB设计的时候,光绘设置是输出生产文件必要的流程,设置好光绘之后,如何对光绘重新命名,如下图 如何把L1改成TOP,L6改成BOTTOM,具体操作步骤如下 点击Manufacture选择Artwork...

[PMLR 2018] Hyperbolic entailment cones for learning hierarchical embeddings
Contents IntroductionEntailment Cones in the Poincar BallConvex cones in a complete Riemannian manifoldAngular cones in the Poincar ballfour intuitive propertiesClosed form expression of the optimal ψ \psi...

2023春季露营投影怎么选?轻薄投影极米Z6X Pro值得推荐
近年来,露营经济在多重因素的共同助推下快速发展,精致露营的攻略开始占据小红书、微博、朋友圈等各类社交平台,吸引着更多用户种草并加入到露营大军中,而露营经济的强势“破圈”给家用智能投影带来了更多的发展契机。凭借着小巧的…...
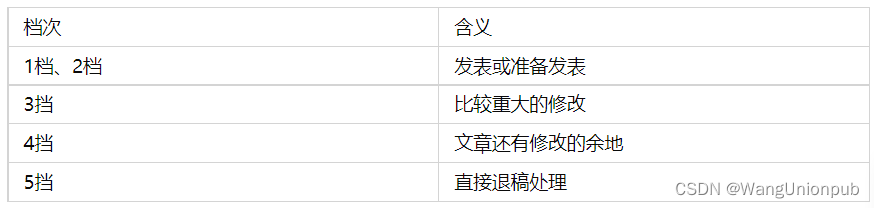
收藏,核心期刊的投稿、审稿、出刊流程详解
学术期刊论文(核心和普刊)的发表流程总的来说其实是一样的,整个流程包括:1写作-2选择刊物-3投稿-4审稿-5返修或拒稿-6录用-7出刊-8上网检索。 其中1和2其实顺序是可以调换的,可以选择好刊物再写作,根据刊物…...
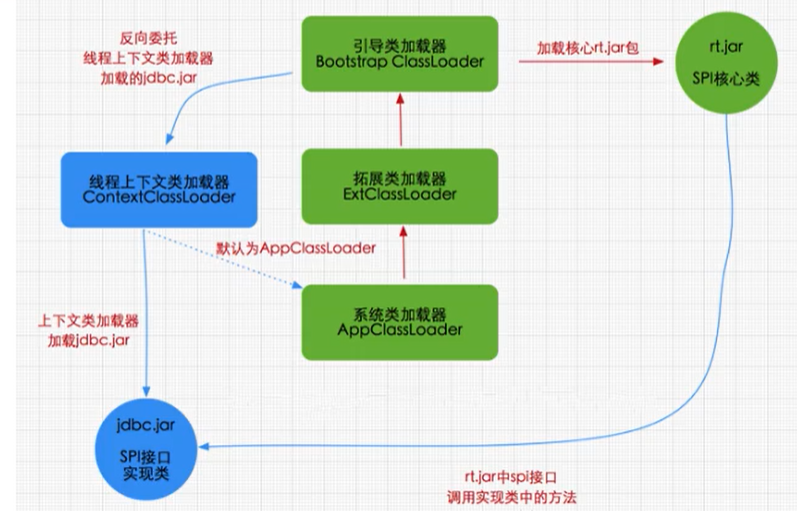
JVM类加载子系统
1、类加载子系统在内存结构中所处的位置通过内存结构图,我们先知道类加载子系统所处的位置,做到心中有图。2、类加载器作用类加载器子系统负责从文件系统或者网络中加载Class文件,class文件在文件开头有特定的文件标识。ClassLoader只负责cla…...

摄像头的镜头的几个知识点
1、镜头的组成及镜片的固定方式 摄像头的镜头结构主要分为镜身,透镜,变焦环,对焦环,光圈叶片,部分还有防抖系统.其中最重要的就是透镜,也叫镜片。镜片的主要原料是光学玻璃,玻璃&…...
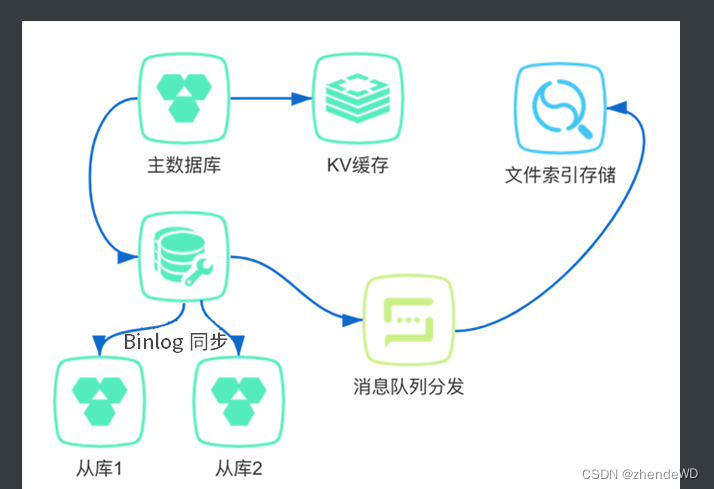
分布式-分布式存储笔记
读写分离 什么时候需要读写分离 互联网大部分业务场景都是读多写少的,读和写的请求对比可能差了不止一个数量级。为了不让数据库的读成为业务瓶颈,同时也为了保证写库的成功率,一般会采用读写分离的技术来保证。 读写分离的实现是把访问的压…...
第十三届蓝桥杯国赛 C++ C 组 Java A 组 C 组 Python C 组 E 题——斐波那契数组(三语言代码AC)
目录1.斐波那契数组1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路3.Ac_code1.Java2.C3.Python1.斐波那契数组 1.题目描述 如果数组 A(a0,a1,⋯.an−1)A(a_0,a_1,⋯.a_{n-1})A(a0,a1,⋯.an−1)满足以下条件, 就说它是一个斐波那契…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
