简历制作方面的经验与建议
专栏推荐:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录
专栏首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录
专栏内容:
- 笔试复盘篇
2023秋招过程中整理的笔试题,来源包括我自己求职笔试以及整理其他同学的笔试。包含华为、中兴、联发科、AMD、大疆、紫光展锐、荣耀、小米、复旦微、星宸、燧原、泰凌微、思特微、瑞芯微、诺瓦、芯合、芯动、芯原、曦华等等公司。 - 面试复盘篇
2023秋招过程中自己的面试,主要包括面试全程的问题与我的回答,以及后期自我点评等。包括华为、中兴、小米、zeku、联发科、星宸、禾赛、加特兰、速腾聚创、地平线、芯原等公司。 - 准备工作篇
包括求职过程中使用到的资料推荐,个人对找工作过程简历制作建议、笔试面试准备经验等。 - 知识整理篇
自己在秋招过程总结的知识点。主要包含 数字电路基础知识、FPGA内部结构知识点、Verilog语法考点、HDL设计知识点、时序分析、SystemVerilog语法、数字IC基础知识等在秋招之前学习以及笔试面试的过程中不断添加的知识点。
本文仅是个人求职过程中的心得体会,内容不一定完全正确,仅供参考。
文章目录
- 1 外观
- 2 内容
- 1.1 个人
相关文章:

简历制作方面的经验与建议
专栏推荐:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 专栏首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 专栏内容: 笔试复盘篇 2023秋招过程中整理的笔试题,来源包括我自己求职笔试以及整理其他同学的笔试。包含华为、中兴、联发科、AMD、大…...

C语言--static、const、volatile关键字
Static static修饰局部变量改变了变量的生命周期,让静态局部变量出了作用域依然存在,到程序结束,生命周期才结束。 static 修饰局部变量 改变局部变量的生命周期,本质上是改变了局部变量的存储位置,让局部变量不再是…...

Rust学习入门--【18】Rust结构体
系列文章目录 Rust 语言是一种高效、可靠的通用高级语言,效率可以媲美 C / C 。本系列文件记录博主自学Rust的过程。欢迎大家一同学习。 Rust学习入门–【1】引言 Rust学习入门–【2】Rust 开发环境配置 Rust学习入门–【3】Cargo介绍 Rust学习入门–【4】Rust 输…...
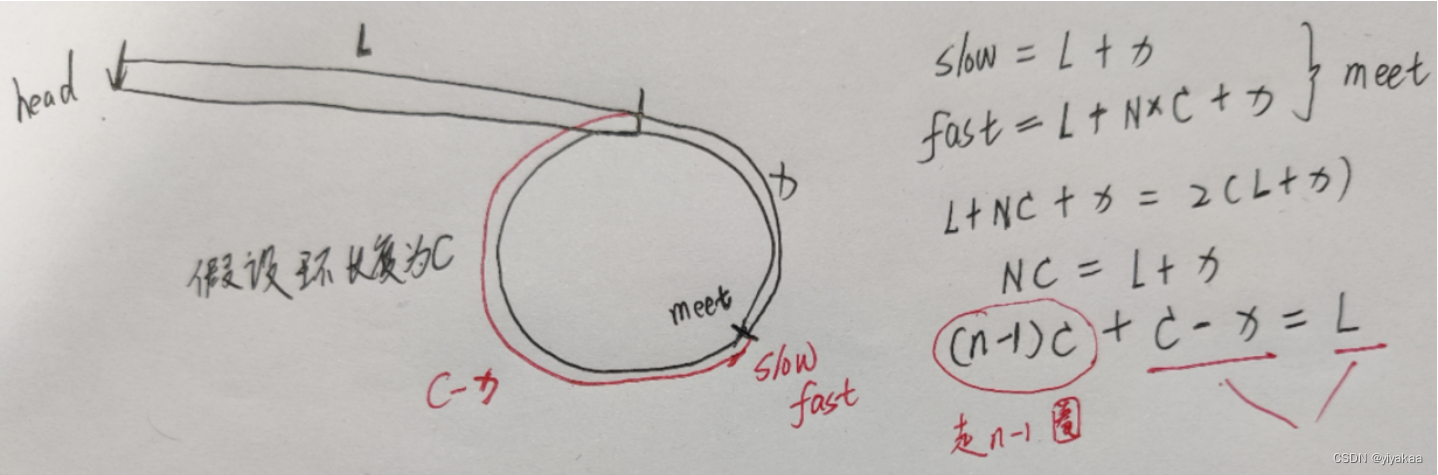
LeetCode142 环形链表Ⅱ
题目: 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评…...

JavaScript刷LeetCode拿offer-高频链表题
首先需要了解链表的概念 先把 next 记录下来 无论是插入,删除,还是翻转等等操作,先把 next 指针用临时变量保存起来,这可以解决 90% 重组链表中指向出错的问题, 如果不知道什么时候需要用到守卫,那就都用…...
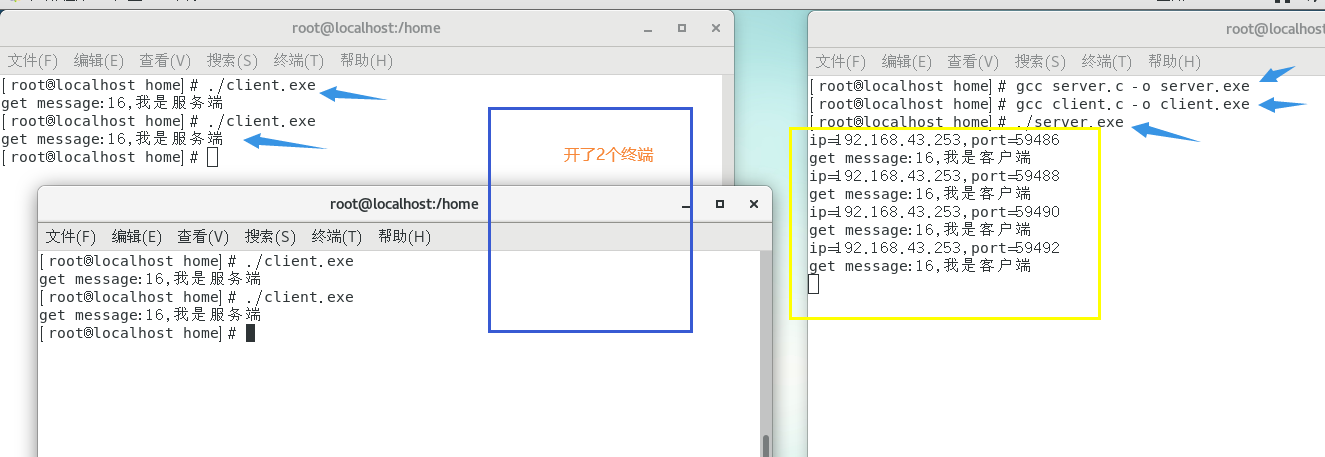
linux系统编程2--网络编程
在linux系统编程中网络编程是使用socket(套接字),socket这个词可以表示很多概念:在TCP/IP协议中,“IP地址TCP或UDP端口号”唯一标识网络通讯中的一个进程,“IP地址端口号”就称为socket。在TCP协议中&#…...
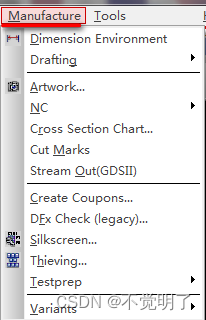
Allegro如何重命名光绘操作指导
Allegro如何重命名光绘操作指导 在做PCB设计的时候,光绘设置是输出生产文件必要的流程,设置好光绘之后,如何对光绘重新命名,如下图 如何把L1改成TOP,L6改成BOTTOM,具体操作步骤如下 点击Manufacture选择Artwork...

[PMLR 2018] Hyperbolic entailment cones for learning hierarchical embeddings
Contents IntroductionEntailment Cones in the Poincar BallConvex cones in a complete Riemannian manifoldAngular cones in the Poincar ballfour intuitive propertiesClosed form expression of the optimal ψ \psi...

2023春季露营投影怎么选?轻薄投影极米Z6X Pro值得推荐
近年来,露营经济在多重因素的共同助推下快速发展,精致露营的攻略开始占据小红书、微博、朋友圈等各类社交平台,吸引着更多用户种草并加入到露营大军中,而露营经济的强势“破圈”给家用智能投影带来了更多的发展契机。凭借着小巧的…...
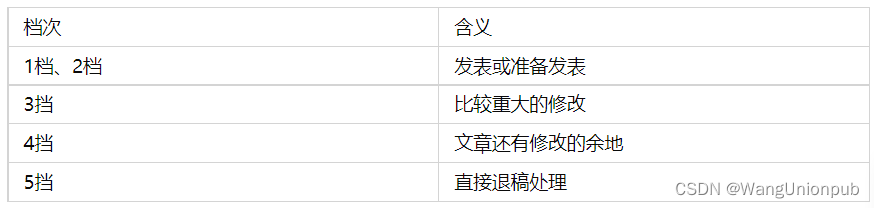
收藏,核心期刊的投稿、审稿、出刊流程详解
学术期刊论文(核心和普刊)的发表流程总的来说其实是一样的,整个流程包括:1写作-2选择刊物-3投稿-4审稿-5返修或拒稿-6录用-7出刊-8上网检索。 其中1和2其实顺序是可以调换的,可以选择好刊物再写作,根据刊物…...
JVM类加载子系统
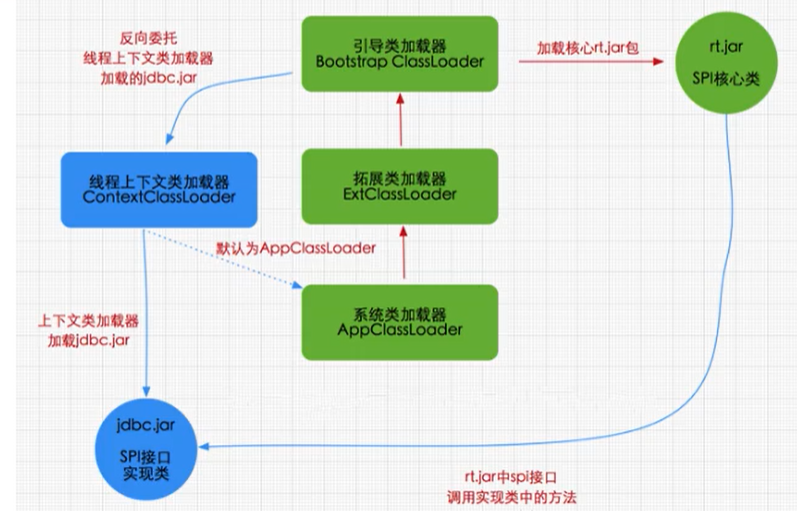
1、类加载子系统在内存结构中所处的位置通过内存结构图,我们先知道类加载子系统所处的位置,做到心中有图。2、类加载器作用类加载器子系统负责从文件系统或者网络中加载Class文件,class文件在文件开头有特定的文件标识。ClassLoader只负责cla…...

摄像头的镜头的几个知识点
1、镜头的组成及镜片的固定方式 摄像头的镜头结构主要分为镜身,透镜,变焦环,对焦环,光圈叶片,部分还有防抖系统.其中最重要的就是透镜,也叫镜片。镜片的主要原料是光学玻璃,玻璃&…...
分布式-分布式存储笔记
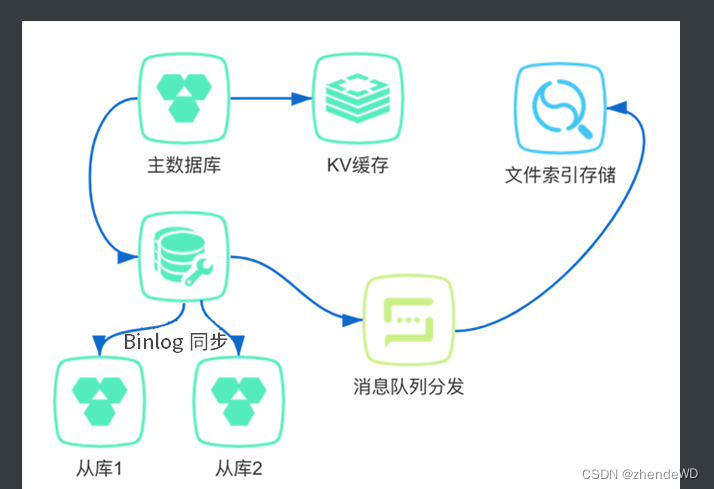
读写分离 什么时候需要读写分离 互联网大部分业务场景都是读多写少的,读和写的请求对比可能差了不止一个数量级。为了不让数据库的读成为业务瓶颈,同时也为了保证写库的成功率,一般会采用读写分离的技术来保证。 读写分离的实现是把访问的压…...
第十三届蓝桥杯国赛 C++ C 组 Java A 组 C 组 Python C 组 E 题——斐波那契数组(三语言代码AC)
目录1.斐波那契数组1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路3.Ac_code1.Java2.C3.Python1.斐波那契数组 1.题目描述 如果数组 A(a0,a1,⋯.an−1)A(a_0,a_1,⋯.a_{n-1})A(a0,a1,⋯.an−1)满足以下条件, 就说它是一个斐波那契…...
多因子模型(MFM)
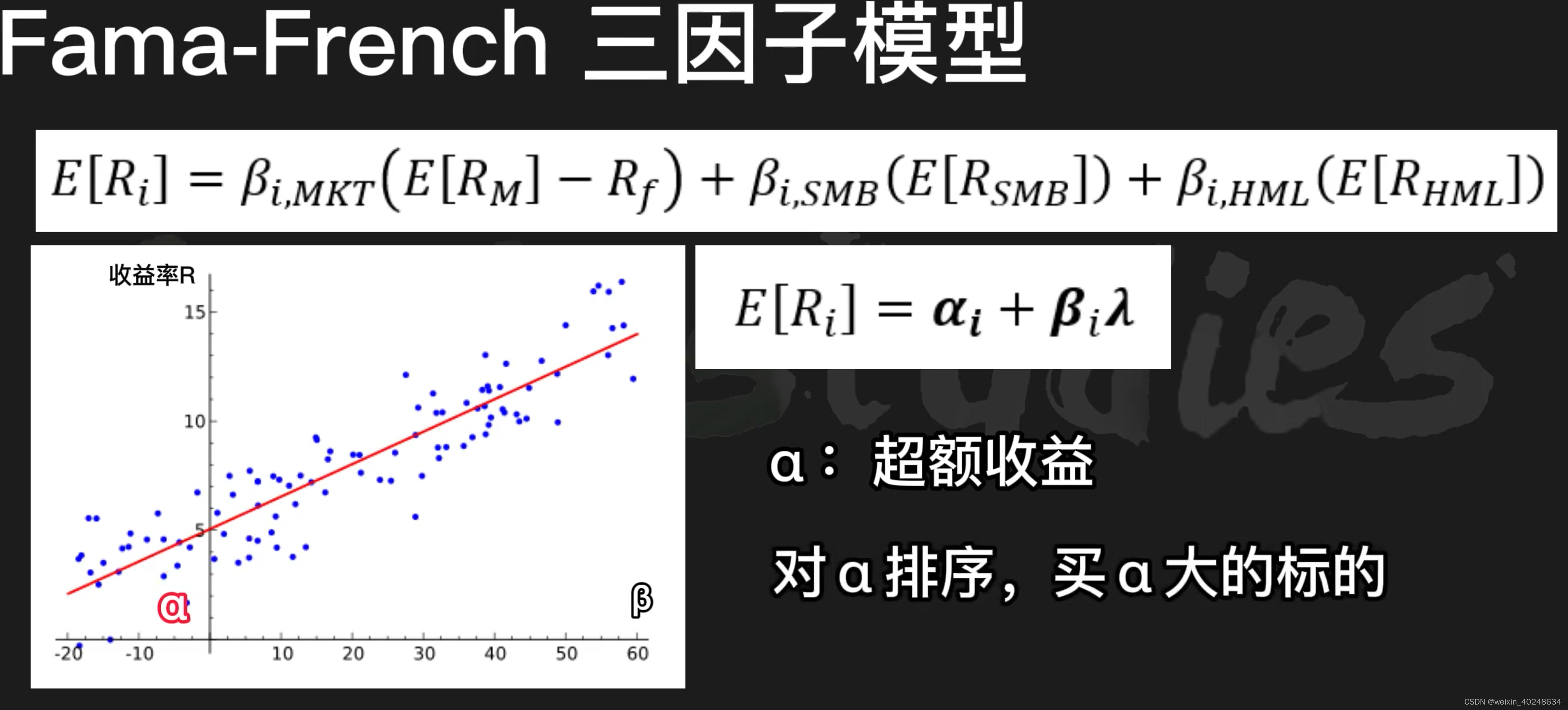
多因子模型(Muiti-Factor M: MFM)因子投资基础CAPM (资本资产定价模型)APT套利定价理论截面数据 & 时间序列数据 & 面板数据定价误差 α\alphaαalpha 出现的原因线性多因子模型Fama-French三因子模型三因子的计算公式利用alpha大小进行购买股票…...

django项目实战一(django+bootstrap实现增删改查)
目录 一、创建django项目 二、修改默认配置 三、配置数据库连接 四、创建表结构 五、在app当中创建静态文件 六、页面实战-部门管理 1、实现一个部门列表页面 2、实现新增部门页面 3、实现删除部门 4、实现部门编辑功能 七、模版的继承 1、创建模板layout.html 1&…...
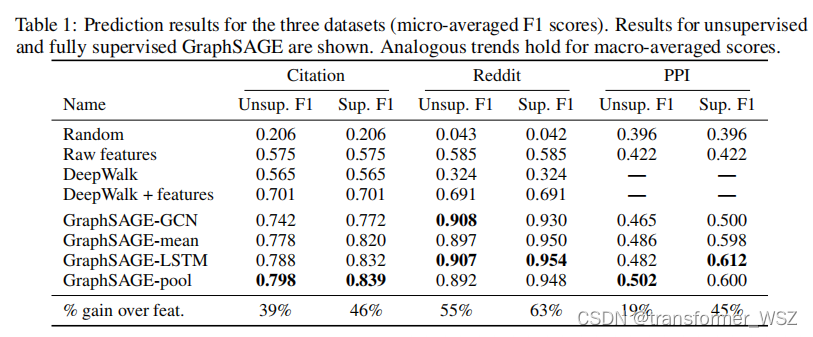
graphsage解读
传统的图方法都是直推式(transductive)的,学习到的是结构固定的图模型,一旦有新的节点加入,便需要重新训练整个图网络,泛化性不强。GraphSAGE是归纳式(inductive)的,它学习一种映射:通过采样和聚合邻居节点…...
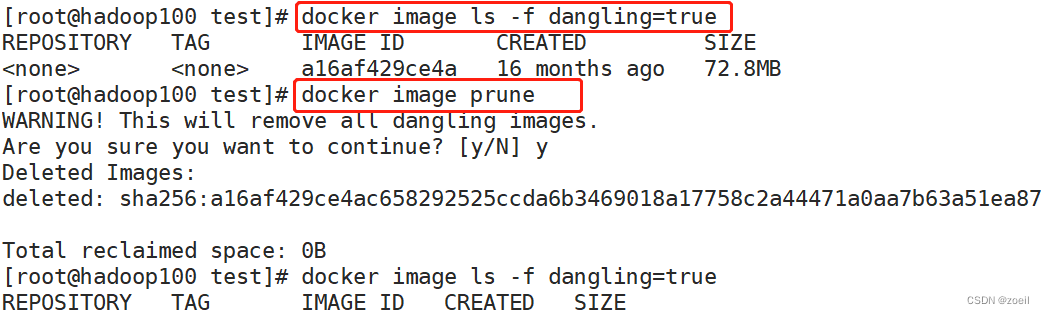
一文带你读懂Dockerfile
目录 一、概述 二、DockerFile构建过程解析 (一)Dockerfile内容基础知识 (二)Docker执行Dockerfile的大致流程 (三)总结 三、DockerFile常用保留字指令 四、案例 (一)自定义…...
用python实现对AES加密的视频数据流解密
密码学中的高级加密标准(Advanced Encryption Standard,AES),又称Rijndael加密法。 在做网络爬虫的时候,会遇到经过AES加密的数据,可以使用python来进行解密。 在做爬虫的时候,通常可以找到一个key,这个key是一个十六进制的一串字符,这传字符是解密的关键。所以对于…...

网络高可用方案
目录 1. 网络高可用 2. 高可用方案设计 2.1 方案一 堆叠 ha负载均衡模式 2.2 方案二 OSPF ha负载均衡模式 3. 高可用保障 1. 网络高可用 网络高可用,是指对于网络的核心部分或设备在设计上考虑冗余和备份,减少单点故障对整个网络的影响。其设计应…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
