数组(八)-- LC[53][152] 最大子数组之和与乘积最大子数组
1 最大子数组之和
1.1 题目描述

题目链接:https://leetcode.cn/problems/maximum-subarray/
1.2 求解思路
1. 暴力法
class Solution:def maxSubArray(self, nums: List[int]) -> int:length = len(nums)max_sum = float('-inf')for i in range(length):sum_sub_array = 0for j in range(i, length):sum_sub_array += nums[j]max_sum = max(max_sum, sum_sub_array)return max_sum

2. 动态规划
关键 1:理解题意
题目要我们找出和最大的连续子数组的值是多少,「连续」是关键字,连续很重要,不是子序列。
题目只要求返回结果,不要求得到最大的连续子数组是哪一个。这样的问题通常可以使用「动态规划」解决。
关键 2:如何定义子问题(如何定义状态)
设计状态思路:把不确定的因素确定下来,进而把子问题定义清楚,把子问题定义得简单。动态规划的思想通过解决了一个一个简单的问题,进而把简单的问题的解组成了复杂的问题的解。
我们 不知道和最大的连续子数组一定会选哪一个数,那么我们可以求出 所有 经过输入数组的某一个数的连续子数组的最大和。
例如,示例 1 输入数组是 [-2,1,-3,4,-1,2,1,-5,4] ,我们可以求出以下子问题:
- 子问题 1:经过 −2 的连续子数组的最大和是多少;
- 子问题 2:经过 1 的连续子数组的最大和是多少;
- 子问题 3:经过 −3 的连续子数组的最大和是多少;
- 子问题 4:经过 4 的连续子数组的最大和是多少;
- 子问题 5:经过 −1 的连续子数组的最大和是多少;
- 子问题 6:经过 2 的连续子数组的最大和是多少;
- 子问题 7:经过 1 的连续子数组的最大和是多少;
- 子问题 8:经过 −5 的连续子数组的最大和是多少;
- 子问题 9:经过 4 的连续子数组的最大和是多少。
一共 9 个子问题,这些子问题之间的联系并没有那么好看出来,这是因为 子问题的描述还有不确定的地方(这件事情叫做「有后效性」,我们在本文的最后会讲解什么是「无后效性」)。
例如「子问题 3」:经过 −3 的连续子数组的最大和是多少。
「经过 −3 的连续子数组」我们任意举出几个:
- [-2,1,-3,4] ,−3 是这个连续子数组的第 3 个元素;
- [1,-3,4,-1] ,−3 是这个连续子数组的第 2 个元素;
- ……
我们不确定的是:−3 是连续子数组的第几个元素。那么我们就把 -3 定义成连续子数组的最后一个元素。在新的定义下,我们列出子问题如下:
- 子问题 1:以 −2 结尾的连续子数组的最大和是多少;
- 子问题 2:以 1 结尾的连续子数组的最大和是多少;
- 子问题 3:以 −3 结尾的连续子数组的最大和是多少;
- 子问题 4:以 4 结尾的连续子数组的最大和是多少;
- 子问题 5:以 −1 结尾的连续子数组的最大和是多少;
- 子问题 6:以 2 结尾的连续子数组的最大和是多少;
- 子问题 7:以 1 结尾的连续子数组的最大和是多少;
- 子问题 8:以 −5 结尾的连续子数组的最大和是多少;
- 子问题 9:以 4 结尾的连续子数组的最大和是多少。
我们加上了「结尾的」,这些子问题之间就有了联系。我们单独看子问题 1 和子问题 2:
- 子问题 1:以 −2 结尾的连续子数组的最大和是多少;
以 −2 结尾的连续子数组是 [-2],因此最大和就是 −2。 - 子问题 2:以 1 结尾的连续子数组的最大和是多少;
以 1 结尾的连续子数组有 [-2,1] 和 [1] ,其中 [-2,1] 就是在「子问题 1」的后面加上 1 得到。−2+1=−1<1-2 + 1 = -1 < 1−2+1=−1<1,因此「子问题 2」 的答案是 1。
大家发现了吗,如果编号为 iii 的子问题的结果是负数或者 0 ,那么编号为 i+1i + 1i+1 的子问题就可以把编号为 iii 的子问题的结果舍弃掉(这里 iii 为整数,最小值为 1 ,最大值为 8),这是因为:
- 一个数 a 加上负数的结果比 a 更小;
- 一个数 a 加上 0 的结果不会比 a 更大;
- 而子问题的定义必须以一个数结尾,因此如果子问题 i 的结果是负数或者 0,那么子问题 i+1i + 1i+1 的答案就是以 nums[i] 结尾的那个数。
因为我们把子问题定义的更清楚,子问题之间的联系就容易观察到。这是我们定义子问题、定义状态的经验。
接下来我们按照编写动态规划题解的步骤,把「状态定义」「状态转移方程」「初始化」「输出」「是否可以空间优化」全都写出来。
定义状态(定义子问题)
dp[i]:表示以 nums[i] 结尾 的 连续 子数组的最大和。
说明:「结尾」和「连续」是关键字。
状态转移方程(描述子问题之间的联系)
根据状态的定义,由于 nums[i] 一定会被选取,并且以 nums[i] 结尾的连续子数组与以 nums[i−1]nums[i-1]nums[i−1] 结尾的连续子数组只相差一个元素 nums[i] 。
假设数组 nums 的值全都严格大于 0,那么一定有 dp[i]=dp[i−1]+nums[i]dp[i] = dp[i - 1] + nums[i]dp[i]=dp[i−1]+nums[i]。
可是 dp[i−1]dp[i-1]dp[i−1] 有可能是负数,于是分类讨论:
- 如果 dp[i−1]>0dp[i - 1] > 0dp[i−1]>0,那么可以把 nums[i] 直接接在 dp[i−1]dp[i - 1]dp[i−1] 表示的那个数组的后面,得到和更大的连续子数组;
- 如果 dp[i−1]<=0dp[i - 1] <= 0dp[i−1]<=0,那么 nums[i] 加上前面的数 dp[i−1]dp[i - 1]dp[i−1] 以后值不会变大。于是 dp[i] 「另起炉灶」,此时单独的一个 nums[i] 的值,就是 dp[i]。
以上两种情况的最大值就是 dp[i] 的值,写出如下状态转移方程:
dp[i]={dp[i−1]+nums[i],ifdp[i−1]>0nums[i],ifdp[i−1]≤0dp[i] = \begin{cases} dp[i - 1] + nums[i], & if \quad dp[i - 1] > 0 \\ nums[i], & if \quad dp[i - 1] \le 0 \end{cases}dp[i]={dp[i−1]+nums[i],nums[i],ifdp[i−1]>0ifdp[i−1]≤0
记为「状态转移方程 1」。
状态转移方程还可以这样写,反正求的是最大值,也不用分类讨论了,就这两种情况,取最大即可,因此还可以写出状态转移方程如下:
dp[i]=max{nums[i],dp[i−1]+nums[i]}dp[i] = \max \{nums[i],\; dp[i - 1] + nums[i]\}dp[i]=max{nums[i],dp[i−1]+nums[i]}
记为「状态转移方程 2」。
友情提示: 求解动态规划的问题经常要分类讨论,这是因为动态规划的问题本来就有「最优子结构」的特点,即大问题的最优解通常由小问题的最优解得到。因此我们在设计子问题的时候,就需要把求解出所有子问题的结果,进而选出原问题的最优解。
思考初始值
dp[0] 根据定义,只有 1 个数,一定以 nums[0] 结尾,因此 dp[0]=nums[0]dp[0] = nums[0]dp[0]=nums[0]。
思考输出
注意:
这里状态的定义不是题目中的问题的定义,不能直接将最后一个状态返回回去;这个问题的输出是把所有的 dp[0]、dp[1]、……、dp[n - 1] 都看一遍,取最大值。
class Solution:def maxSubArray(self, nums: List[int]) -> int:size = len(nums)if size == 0:return 0dp = [0 for _ in range(size)]dp[0] = nums[0]for i in range(1, size):if dp[i - 1] >= 0:dp[i] = dp[i - 1] + nums[i]else:dp[i] = nums[i]return max(dp)
进一步优化空间:
from typing import Listclass Solution:def maxSubArray(self, nums: List[int]) -> int:size = len(nums)pre = 0res = nums[0]for i in range(size):pre = max(nums[i], pre + nums[i])res = max(res, pre)return res

3. 贪心算法
class Solution:def maxSubArray(self, nums: List[int]) -> int:# 时间复杂度:O(n), 遍历了一遍# 空间复杂度:O(1), 用了2个变量cur_sum = nums[0]max_sum = nums[0]# range范围是[1,len(nums)) 左闭右开,切记切记for i in range(1,len(nums)):# 若当前指针指向元素之前的和小于0,则丢弃此元素之前的数列(拖后腿的丢弃!!!)# 当前和=当前值 与 当前值+之前最大和 的比较中较大的那个、# 通俗易懂的理解:看当前这个值和之前数列的和,是否会拖当前这个值的后腿,如果扯后腿了说明没必要把之前的数列放到当前和,如果没有扯后腿则把最新的较大数放在当前和里面cur_sum = max(nums[i], cur_sum+nums[i])# 最大和=当前和 与 最大和 的比较中较大的那个# 通俗易懂的理解:当前和就相当于当前潜在的最大和,把原来的最大和 与当前的潜在最大和进行比较,如果当前和比较大,则更换最大和,否则不更换max_sum = max(cur_sum, max_sum)return max_sum

4. 分治法
连续子序列的最大和主要由这三部分子区间里元素的最大和得到:
- 第 1 部分:子区间 [left,mid][left, mid][left,mid];
- 第 2 部分:子区间 [mid+1,right][mid + 1, right][mid+1,right];
- 第 3 部分:包含子区间 [mid,mid+1][mid , mid + 1][mid,mid+1] 的子区间,即 nums[mid] 与 nums[mid + 1] 一定会被选取。
对这三个部分求最大值即可
from typing import Listclass Solution:def maxSubArray(self, nums: List[int]) -> int:size = len(nums)if size == 0:return 0return self.__max_sub_array(nums, 0, size - 1)def __max_sub_array(self, nums, left, right):if left == right:return nums[left]mid = (left + right) >> 1return max(self.__max_sub_array(nums, left, mid),self.__max_sub_array(nums, mid + 1, right),self.__max_cross_array(nums, left, mid, right))def __max_cross_array(self, nums, left, mid, right):# 一定包含 nums[mid] 元素的最大连续子数组的和,# 思路是看看左边"扩散到底",得到一个最大数,右边"扩散到底"得到一个最大数# 然后再加上中间数left_sum_max = 0start_left = mid - 1s1 = 0while start_left >= left:s1 += nums[start_left]left_sum_max = max(left_sum_max, s1)start_left -= 1right_sum_max = 0start_right = mid + 1s2 = 0while start_right <= right:s2 += nums[start_right]right_sum_max = max(right_sum_max, s2)start_right += 1return left_sum_max + nums[mid] + right_sum_max

2 乘积最大子数组
2.1 题目描述

题目链接:https://leetcode.cn/problems/maximum-product-subarray/description/
2.2 求解思路
如果我们用 fmax(i)f_{\max}(i)fmax(i) 来表示以第 iii 个元素结尾的乘积最大子数组的乘积,aaa 表示输入参数 nums,那么根据前面「53. 最大子序和」的经验,我们很容易推导出这样的状态转移方程:
fmax(i)=maxi=1n{f(i−1)×ai,ai}f_{\max}(i) = \max_{i = 1}^{n} \{ f(i - 1) \times a_i, a_i \}fmax(i)=i=1maxn{f(i−1)×ai,ai}
它表示以第 iii 个元素结尾的乘积最大子数组的乘积可以考虑 aia_iai 加入前面的 fmax(i−1)f_{\max}(i - 1)fmax(i−1) 对应的一段,或者单独成为一段,这里两种情况下取最大值。求出所有的 fmax(i)f_{\max}(i)fmax(i) 之后选取最大的一个作为答案。
可是在这里,这样做是错误的。为什么呢?
因为这里的定义并不满足「最优子结构」。具体地讲,如果 a={5,6,−3,4,−3}a = \{ 5, 6, -3, 4, -3 \}a={5,6,−3,4,−3},那么此时 fmaxf_{\max}fmax 对应的序列是 {5,30,−3,4,−3}\{ 5, 30, -3, 4, -3 \}{5,30,−3,4,−3},按照前面的算法我们可以得到答案为 30,即前两个数的乘积,而实际上答案应该是全体数字的乘积。我们来想一想问题出在哪里呢?问题出在最后一个 −3 所对应的 fmaxf_{\max}fmax 的值既不是 −3,也不是 4×(−3)4 \times (-3)4×(−3),而是 5×6×(−3)×4×(−3)5 \times 6 \times (-3) \times 4 \times (-3)5×6×(−3)×4×(−3)。所以我们得到了一个结论:当前位置的最优解未必是由前一个位置的最优解转移得到的。
我们可以根据正负性进行分类讨论。
考虑当前位置如果是一个负数的话,那么我们希望以它前一个位置结尾的某个段的积也是个负数,这样就可以负负得正,并且我们希望这个积尽可能「负得更多」,即尽可能小。如果当前位置是一个正数的话,我们更希望以它前一个位置结尾的某个段的积也是个正数,并且希望它尽可能地大。于是这里我们可以再维护一个 fmin(i)f_{\min}(i)fmin(i),它表示以第 iii 个元素结尾的乘积最小子数组的乘积,那么我们可以得到这样的动态规划转移方程:
fmax(i)=maxi=1n{fmax(i−1)×ai,fmin(i−1)×ai,ai}fmin(i)=mini=1n{fmax(i−1)×ai,fmin(i−1)×ai,ai}\begin{aligned} f_{\max}(i) &= \max_{i = 1}^{n} \{ f_{\max}(i - 1) \times a_i, f_{\min}(i - 1) \times a_i, a_i \} \\ f_{\min}(i) &= \min_{i = 1}^{n} \{ f_{\max}(i - 1) \times a_i, f_{\min}(i - 1) \times a_i, a_i \} \end{aligned} fmax(i)fmin(i)=i=1maxn{fmax(i−1)×ai,fmin(i−1)×ai,ai}=i=1minn{fmax(i−1)×ai,fmin(i−1)×ai,ai}
它代表第 iii 个元素结尾的乘积最大子数组的乘积 fmax(i)f_{\max}(i)fmax(i),可以考虑把 aia_iai 加入第 i−1i - 1i−1 个元素结尾的乘积最大或最小的子数组的乘积中,二者加上 aia_iai,iii 个元素结尾的乘积最大子数组的乘积。第 iii 个元素结尾的乘积最小子数组的乘积 fmin(i)f_{\min}(i)fmin(i) 同理。
class Solution:def maxProduct(self, nums: List[int]) -> int:max_dp, min_dp = [nums[0]], [nums[0]]for i in range(1, len(nums)):max_dp.append(max(max_dp[i-1]*nums[i], min_dp[i-1]*nums[i], nums[i]))min_dp.append(min(max_dp[i-1]*nums[i], min_dp[i-1]*nums[i], nums[i]))return max(max_dp)
进一步优化:
class Solution:def maxProduct(self, nums: List[int]) -> int:'''动态规划'''max_product, min_product, ans = nums[0], nums[0], nums[0]for num in nums[1:]:max_nums, min_nums = max_product, min_productmax_product = max(max_nums*num, min_nums*num, num)min_product = min(max_nums*num, min_nums*num, num)ans = max(ans, max_product)return ans
参考
- 经典动态规划问题(理解「无后效性」):https://leetcode.cn/problems/maximum-subarray/solutions/9058/dong-tai-gui-hua-fen-zhi-fa-python-dai-ma-java-dai/?orderBy=most_votes
相关文章:

数组(八)-- LC[53][152] 最大子数组之和与乘积最大子数组
1 最大子数组之和 1.1 题目描述 题目链接:https://leetcode.cn/problems/maximum-subarray/ 1.2 求解思路 1. 暴力法 class Solution:def maxSubArray(self, nums: List[int]) -> int:length len(nums)max_sum float(-inf)for i in range(length):sum_sub_…...
docker2-zabbix
安装最新版docker yum remove docker docker-common docker-selinux docker-engine yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo yum makecache fast yum list docker-ce --showduplicates | sort -r yum install docke…...

ctcdecode安装
1.下载 https://pan.baidu.com/s/1sZMbzzYtBoT35zHtDifVqQ ,提取码:a05y。然后解压到ctcdecode文件夹中。 感谢 ctcdecode安装_huangneng0219的博客-CSDN博客 提供。 然后build.py文件中的compile_args [-O3, -DKENLM_MAX_ORDER6, -stdc11, -fPIC] …...

虚树学习小记
虚树是什么 虚树指在原树上选择需要的点和它们的LCALCALCA组成的一棵树。这样可以使在树DP时顶点数更少,从而减少时间复杂度。一般用于有多组数据且能保证所有数据访问的点的和不超过规定范围。 情景代入:SDOI2011消耗战 SDOI2011消耗战 题目大意 给…...

【C++】特殊类设计(单例模式)
文章目录一、设计模式概念二、设计一个不能被拷贝的类三、设计一个只能在堆上创建对象的类3.1 私有构造3.2 私有析构四、设计一个只能在栈上创建对象的类五、设计不能被继承的类六、单例模式❗️❗️6.1 饿汉模式6.2 懒汉模式6.2.1 线程安全问题6.2.2 新写法一、设计模式概念 …...
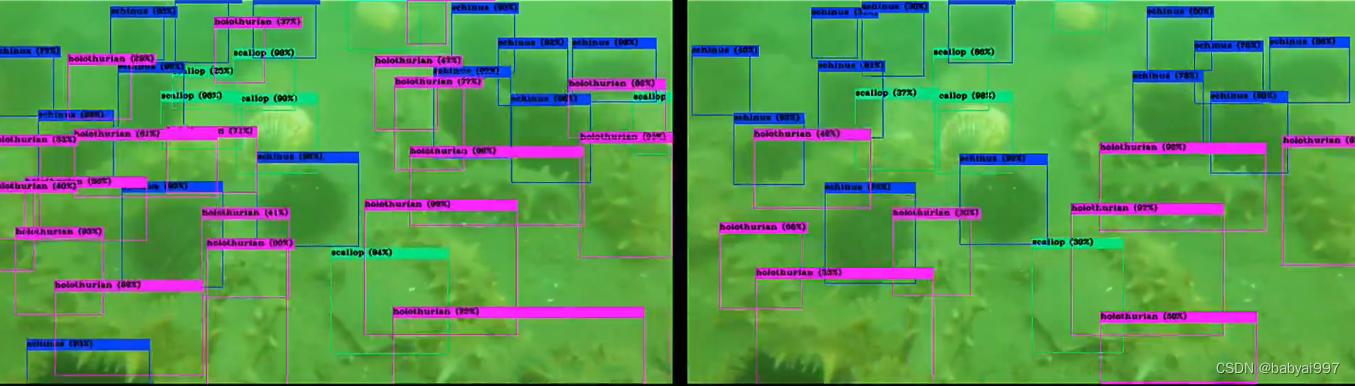
基于YOLOv5的水下海洋目标检测
摘要:水下海洋目标检测技术具有广泛的应用前景,可以用于海洋环境监测、海洋资源开发、海洋生物学研究等领域。本文提出了一种基于 YOLOv5 的水下海洋目标检测方法,使用数据增强方法进行了大量实验,并与其他方法进行了对比…...
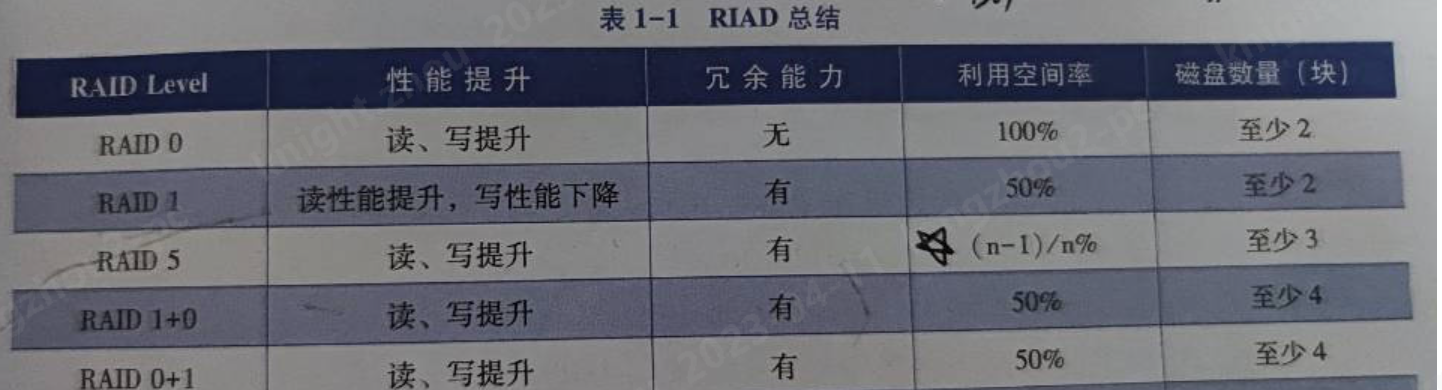
磁盘这列(Raid)
RAID介绍 RAID技术通过把多个硬盘设备组合成一个容量更大的、安全性更好的磁盘阵列。把数据切割成许多区段后分别放在不同的物理磁盘上,然后利用分散读写技术来提升磁盘阵列整体的性能,同时把多个重要数据的副本同步到不同的物理设备上,从而…...
)
Oracle之PL/SQL存储过程与函数练习题(七)
1.创建一个存储过程,以员工号为参数,输出该员工的工资2.创建一个存储过程,以员工号为参数,修改该员工的工资。若该员工属于10号部门,则工资增加150;若属于20号部门,则工资增加200;若…...

C++入门教程||C++ 基本的输入输出||C++ 数据结构
C 基本的输入输出 C 基本的输入输出 C 标准库提供了一组丰富的输入/输出功能,我们将在后续的章节进行介绍。本章将讨论 C 编程中最基本和最常见的 I/O 操作。 C 的 I/O 发生在流中,流是字节序列。如果字节流是从设备(如键盘、磁盘驱动器、…...
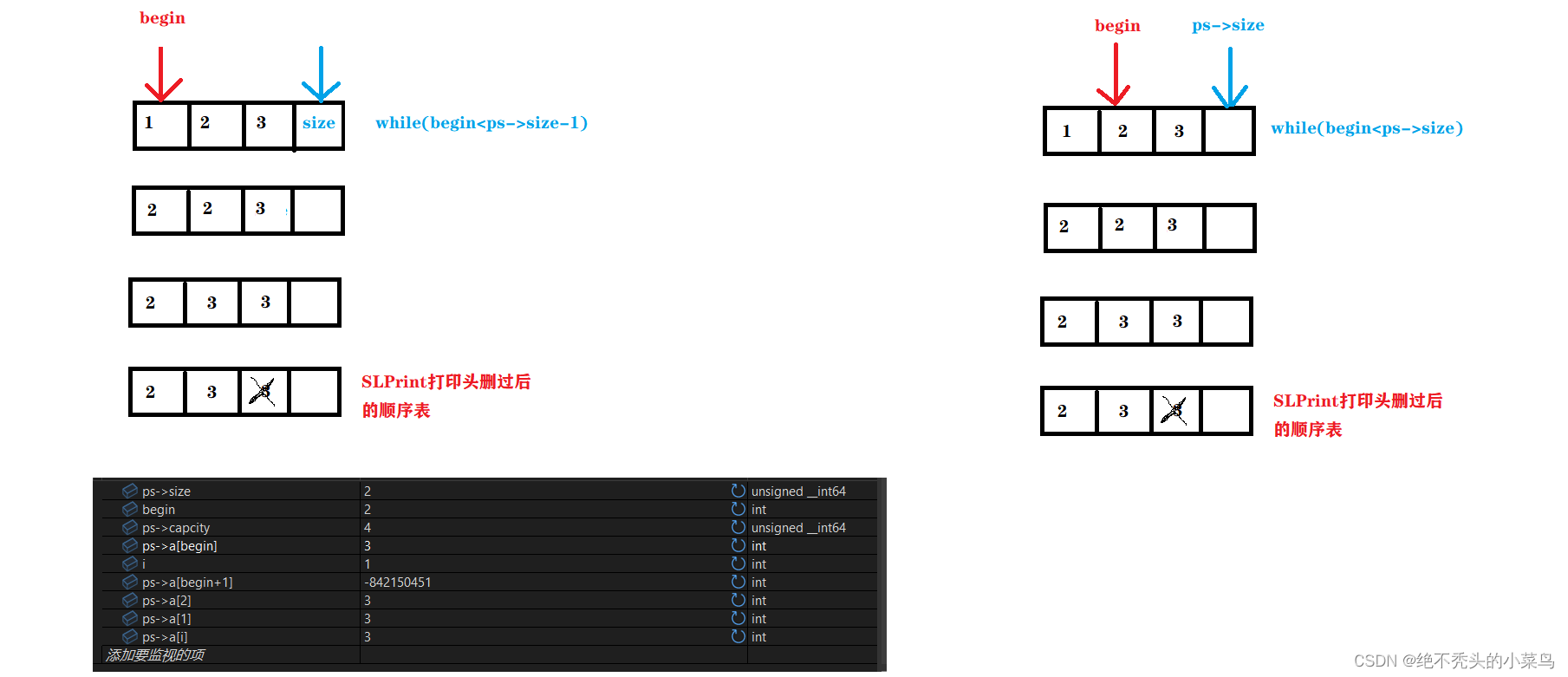
线性表——顺序表
文章目录一:线性表二:顺序表1:概念与结构1:静态顺序表2:动态顺序表2:动态顺序表的代码实现1:结构2:接口实现1:初始化2:释放内存3:检查容量4&#…...

第六章 Vite4+Vue3+Vtkjs 模型颜色切换、漫反射曲面颜色
一、介绍 💥 💥 Vtk里面工具非常的齐全,但是相关的文档又少之又少,只能花大量时间去阅读源码。漫反射曲面颜色是什么意思呢,Vtk可以使用漫反射曲面颜色来模拟光线在表面反射时的颜色。漫反射是一种光线与表面发生碰撞后,被散射到各个方向的现象,这种现象可以用来解释物…...

【QT学习七】QTreeWidget
目录 一、QTreeWidget 概述 二、QTreeWidget 的基本使用 2.1、创建 QTreeWidget 控件 2.2、设置 QTreeWidget 的大小和位置 2.3、设置 QTreeWidget 的列数和列标题 2.4、添加节点 2.5、读取节点 2.6、设置节点数据 2.7、自定义节点样式 三、注意事项 四、完整示例 一…...
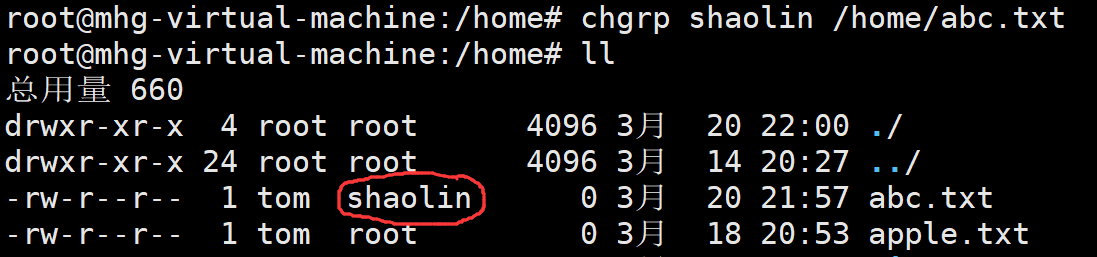
【Linux】组管理和权限管理
目录1 Linux组的基本介绍2 文件/目录所有者2.1 查看文件的所有者2.2 修改文件所有者3 组的创建3.1 基本指令3.2 应用实例4 文件/目录 所在组4.1 查看文件/目录所在组4.2修改文件/目录所在的组5 其他组6 改变用户所在组6.1 改变用户所在的组6.2 应用实例7 权限介绍8 rwx权限详解…...

从零到一发布 NPM 包
如果你负责前端的基础能力建设,发布各种功能/插件包犹如家常便饭,所以熟悉对 npm 包的发布与管理是非常有必要的,故此有了本篇总结文章。本篇文章一方面总结,一方面向社区贡献开箱即用的 npm 开发、编译、发布、调试模板ÿ…...
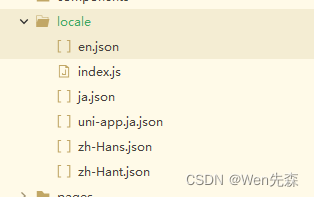
uniapp国际化配置
1、创建资源文件 创建一个locale文件夹,新增index.js,en.json,zh-hans.json 2.配置locale文件夹中的index.js文件 import Vue from vue import VueI18n from vue-i18n// v8.x import en from ./en.json import zhHans from ./zh-Hans.json import zhHant from .…...
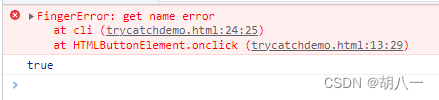
前端中 try-catch 捕获不到哪些异常和常见错误
在开发过程中,我们的目标是 0error,0warning。 但有很多因素并不是我们可控的,为了避免某块代码的错误,影响到其他模块或者整体代码的运行,我们经常会使用try-catch模块来主动捕获一些异常或者错误。 比如我们在获取…...

javaEE 初阶 — 如何构造一个 HTTP 请求
文章目录使用 form 表单标签构造1 构造 GET 请求2 构造 POST 请求使用 ajax 构造1 什么是异步2 代码中如何使用 ajax使用第三方工具构造1 postman 工具的安装2 postman 工具的使用使用 form 表单标签构造 1 构造 GET 请求 使用 form 表单构造 HTTP 请求,需要用到两…...

CentOS 7下安装PostgreSQL 15版本数据库(图文详细)
文章目录CentOS 7下安装PostgreSQL 15版本数据库(图文详细)1 简介1.1 概述1.2 官网2 PostgreSQL安装2.1 选定版本2.2 安装依赖2.3 执行安装2.4 初始化2.5 配置环境变量2.6 创建数据库2.6.1 进入命令行2.6.2 创建DB2.6.3 设置密码2.7 配置远程2.8 测试链接3 pgAdmin4工具安装3.1…...

代码随想录算法训练营第五十一天 | 309. 最佳买卖股票时机含冷冻期、714. 买卖股票的最佳时机含手续费
309. 最佳买卖股票时机含冷冻期 动规五部曲 1、确定dp数组以及下标的含义 dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。 具体可以区分出如下四个状态: 状态一:持有股票状态(今天买入股票,或者是…...

中英文拼写检测纠正开源项目使用入门 word-checker 1.1.0
项目简介 word-checker 本项目用于单词拼写检查。支持英文单词拼写检测,和中文拼写检测。 特性说明 可以迅速判断当前单词是否拼写错误 可以返回最佳匹配结果 可以返回纠正匹配列表,支持指定返回列表的大小 错误提示支持 i18n 支持大小写、全角半角…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
