虚树学习小记
虚树是什么
虚树指在原树上选择需要的点和它们的LCALCALCA组成的一棵树。这样可以使在树DP时顶点数更少,从而减少时间复杂度。一般用于有多组数据且能保证所有数据访问的点的和不超过规定范围。
情景代入:SDOI2011消耗战
SDOI2011消耗战
题目大意
给出一棵树,根节点为一号点,有nnn顶点,n−1n-1n−1条边,每条边都有边权,断掉一条边的代价为这条边的边权。有mmm次询问,每次询问给出kkk个询问点,问使这kkk个点都不和根节点相连的最小代价。
数据范围
1≤n≤2.5×105,1≤m≤5×105,1≤∑k≤5×1051\leq n\leq 2.5\times 10^5,1\leq m\leq 5\times 10^5,1\leq \sum k\leq 5\times 10^51≤n≤2.5×105,1≤m≤5×105,1≤∑k≤5×105
做法
我们可以用树型DP。设f[i]f[i]f[i]表示子树iii与根节点断开的代价,md[i]md[i]md[i]表示点iii到根节点的最小边权。分类讨论一下:
- 如果点iii是询问点,那么f[i]=md[i]f[i]=md[i]f[i]=md[i]
- 如果点iii不是询问点,那么f[i]=min(md[i],∑j∈sonifj)f[i]=min(md[i],\sum\limits_{j\in son_i}f_j)f[i]=min(md[i],j∈soni∑fj)
可以用dfs来解决。
但如果直接这样做的话,时间复杂度为O(nm)O(nm)O(nm),显然会TLE。又因为kkk的和在5×1055\times 10^55×105以内,所以我们可以用虚树来解决。
对于每次询问,我们将询问点和它们的LCALCALCA放到虚树中。举几个例子:
对于如下一棵树

如果查询点为6,10,那么构成的虚树如下

放进虚树的点即为查询点和它们的LCALCALCA。
因为每加入一个点最多只会产生一个LCALCALCA,所以如果有kkk个有效的点,则虚树上最多只会有2k2k2k个点。
虚树如何建立
那么,虚树该如何建立呢?
首先,我们对原树进行dfs,按dfs序给每一个点打上时间戳dfn。
将所有要查询的点按dfn排序,用栈来维护根节点到当前点的链。
一开始,根节点入栈,st[++top]=1st[++top]=1st[++top]=1
设当前加入的点为xxx
- 用whilewhilewhile循环,如果dfn[s[top−1]]≥dfn[lca(s[top],x)]dfn[s[top-1]]\geq dfn[lca(s[top],x)]dfn[s[top−1]]≥dfn[lca(s[top],x)],那么lcalcalca为点st[top]st[top]st[top]的祖先,连边(st[top−1],st[top]),top−−(st[top-1],st[top]),top--(st[top−1],st[top]),top−−
- ififif判断如果dfn[lca(st[top],x)]≠dfn[st[top]]dfn[lca(st[top],x)]\neq dfn[st[top]]dfn[lca(st[top],x)]=dfn[st[top]],则lcalcalca在点st[top]st[top]st[top]和st[top−1]st[top-1]st[top−1]之间,连边(lca,st[top]),st[top]=lca(lca,st[top]),st[top]=lca(lca,st[top]),st[top]=lca,将xxx入栈,然后退出
当所有点都考虑完了之后,还要对栈中的点依次连边并退栈。
code
void insert(int x){if(top==1){s[++top]=x;return;}int lca=LCA(x,s[top]);
// if(lca==s[top]) return;while(top>1&&dfn[s[top-1]]>=dfn[lca]){add(s[top-1],s[top]);--top;}if(lca!=s[top]){add(lca,s[top]);s[top]=lca;}s[++top]=x;
}
其中被注释的一行是一般虚树加点操作没有的,但这道题需要。因为这道题如果一个点一定不与根节点相连,则其子树叶一定满足条件,所以子树可以不用考虑。而在最底部的s[top]s[top]s[top]一定不是LCALCALCA,所以遇到这种情况直接return即可。
加点过程如下
code
dfs(1,0);
while(m--){scanf("%d",&k);for(int i=1;i<=k;i++){scanf("%d",&a[i]);}sort(a+1,a+k+1,cmp);s[top=1]=1;for(int i=1;i<=k;i++){insert(a[i]);}while(top>1){v[s[top-1]].push_back(s[top]);--top;}printf("%lld\n",dp(1));
}
SDOI2011消耗战
用虚树来做的话,时间复杂度为O(∑klogk)O(\sum k\log k)O(∑klogk)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=250000;
int n,m,k,tot=0,dt=0,top,d[500005],l[500005],r[500005];
int a[N+5],s[N+5],fa[N+5],tp[N+5],dep[N+5],siz[N+5],son[N+5],dfn[N+5];
long long w[500005],md[N+5];
vector<int>v[N+5];
bool cmp(int ax,int bx){return dfn[ax]<dfn[bx];
}
void add(int xx,int yy,long long zz){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;w[tot]=zz;
}
void dfs1(int u,int f){dep[u]=dep[f]+1;fa[u]=f;siz[u]=1;for(int i=r[u];i;i=l[i]){if(d[i]==f) continue;md[d[i]]=min(w[i],md[u]);dfs1(d[i],u);siz[u]+=siz[d[i]];if(siz[d[i]]>siz[son[u]]) son[u]=d[i];}
}
void dfs2(int u,int f){dfn[u]=++dt;if(son[u]){tp[son[u]]=tp[u];dfs2(son[u],u);}for(int i=r[u];i;i=l[i]){if(d[i]==f||d[i]==son[u]) continue;tp[d[i]]=d[i];dfs2(d[i],u);}
}
int gt(int x,int y){while(tp[x]!=tp[y]){if(dep[tp[x]]<dep[tp[y]]) swap(x,y);x=fa[tp[x]];}if(dep[x]>dep[y]) swap(x,y);return x;
}
void insert(int x){if(top==1){s[++top]=x;return;}int lca=gt(x,s[top]);if(lca==s[top]) return;while(top>1&&dfn[s[top-1]]>=dfn[lca]){v[s[top-1]].push_back(s[top]);--top;}if(s[top]!=lca){v[lca].push_back(s[top]);s[top]=lca;}s[++top]=x;
}
long long dp(int u){if(v[u].size()==0) return md[u];long long sum=0;for(int i=0;i<v[u].size();i++){sum+=dp(v[u][i]);}v[u].clear();return min(sum,md[u]);
}
int main()
{int x,y;long long z;scanf("%d",&n);md[1]=1e18;for(int i=1;i<n;i++){scanf("%d%d%lld",&x,&y,&z);add(x,y,z);add(y,x,z);}dfs1(1,0);tp[1]=1;dfs2(1,0);scanf("%d",&m);while(m--){scanf("%d",&k);for(int i=1;i<=k;i++){scanf("%d",&a[i]);}sort(a+1,a+k+1,cmp);s[top=1]=1;for(int i=1;i<=k;i++){insert(a[i]);}while(top>1){v[s[top-1]].push_back(s[top]);--top;}printf("%lld\n",dp(1));}return 0;
}
相关文章:

虚树学习小记
虚树是什么 虚树指在原树上选择需要的点和它们的LCALCALCA组成的一棵树。这样可以使在树DP时顶点数更少,从而减少时间复杂度。一般用于有多组数据且能保证所有数据访问的点的和不超过规定范围。 情景代入:SDOI2011消耗战 SDOI2011消耗战 题目大意 给…...

【C++】特殊类设计(单例模式)
文章目录一、设计模式概念二、设计一个不能被拷贝的类三、设计一个只能在堆上创建对象的类3.1 私有构造3.2 私有析构四、设计一个只能在栈上创建对象的类五、设计不能被继承的类六、单例模式❗️❗️6.1 饿汉模式6.2 懒汉模式6.2.1 线程安全问题6.2.2 新写法一、设计模式概念 …...
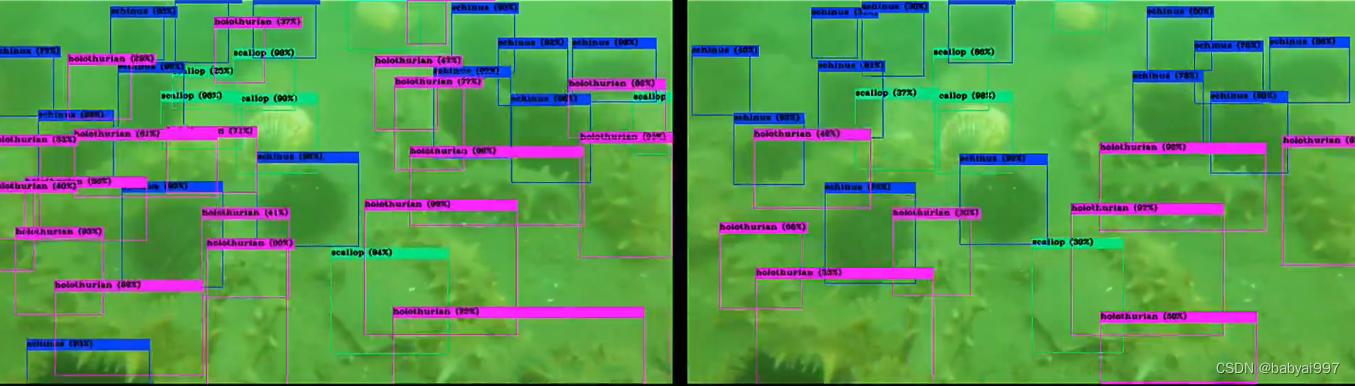
基于YOLOv5的水下海洋目标检测
摘要:水下海洋目标检测技术具有广泛的应用前景,可以用于海洋环境监测、海洋资源开发、海洋生物学研究等领域。本文提出了一种基于 YOLOv5 的水下海洋目标检测方法,使用数据增强方法进行了大量实验,并与其他方法进行了对比…...
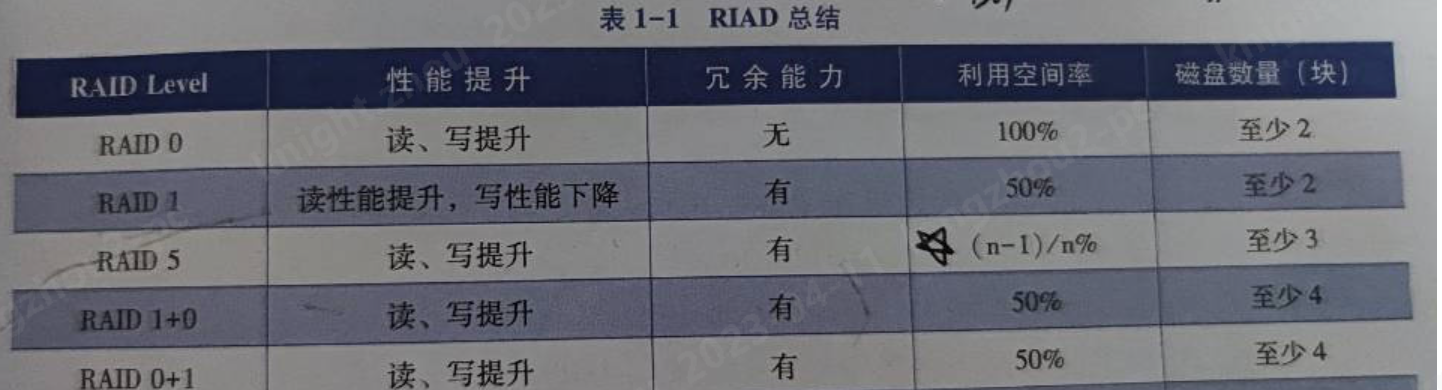
磁盘这列(Raid)
RAID介绍 RAID技术通过把多个硬盘设备组合成一个容量更大的、安全性更好的磁盘阵列。把数据切割成许多区段后分别放在不同的物理磁盘上,然后利用分散读写技术来提升磁盘阵列整体的性能,同时把多个重要数据的副本同步到不同的物理设备上,从而…...
)
Oracle之PL/SQL存储过程与函数练习题(七)
1.创建一个存储过程,以员工号为参数,输出该员工的工资2.创建一个存储过程,以员工号为参数,修改该员工的工资。若该员工属于10号部门,则工资增加150;若属于20号部门,则工资增加200;若…...

C++入门教程||C++ 基本的输入输出||C++ 数据结构
C 基本的输入输出 C 基本的输入输出 C 标准库提供了一组丰富的输入/输出功能,我们将在后续的章节进行介绍。本章将讨论 C 编程中最基本和最常见的 I/O 操作。 C 的 I/O 发生在流中,流是字节序列。如果字节流是从设备(如键盘、磁盘驱动器、…...
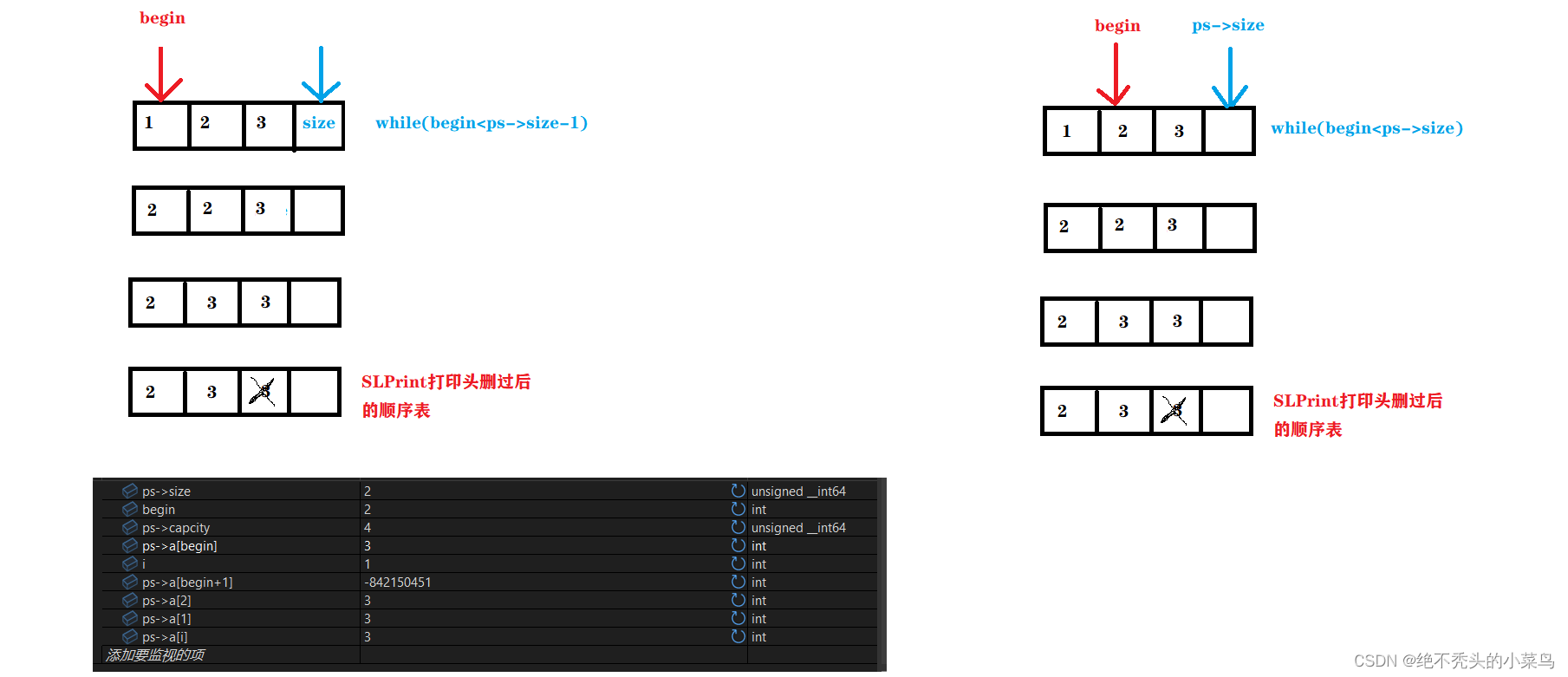
线性表——顺序表
文章目录一:线性表二:顺序表1:概念与结构1:静态顺序表2:动态顺序表2:动态顺序表的代码实现1:结构2:接口实现1:初始化2:释放内存3:检查容量4&#…...

第六章 Vite4+Vue3+Vtkjs 模型颜色切换、漫反射曲面颜色
一、介绍 💥 💥 Vtk里面工具非常的齐全,但是相关的文档又少之又少,只能花大量时间去阅读源码。漫反射曲面颜色是什么意思呢,Vtk可以使用漫反射曲面颜色来模拟光线在表面反射时的颜色。漫反射是一种光线与表面发生碰撞后,被散射到各个方向的现象,这种现象可以用来解释物…...

【QT学习七】QTreeWidget
目录 一、QTreeWidget 概述 二、QTreeWidget 的基本使用 2.1、创建 QTreeWidget 控件 2.2、设置 QTreeWidget 的大小和位置 2.3、设置 QTreeWidget 的列数和列标题 2.4、添加节点 2.5、读取节点 2.6、设置节点数据 2.7、自定义节点样式 三、注意事项 四、完整示例 一…...
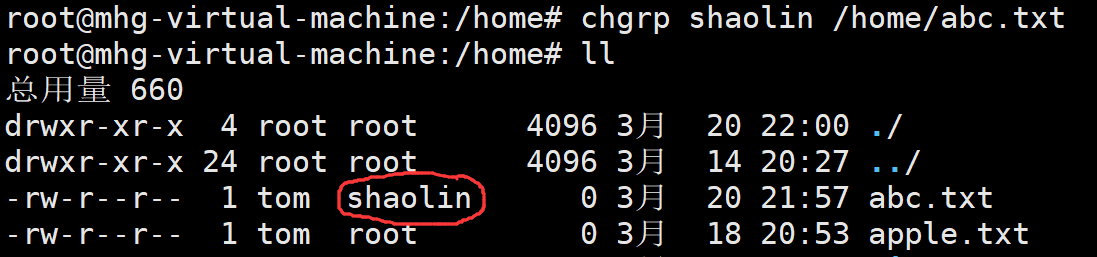
【Linux】组管理和权限管理
目录1 Linux组的基本介绍2 文件/目录所有者2.1 查看文件的所有者2.2 修改文件所有者3 组的创建3.1 基本指令3.2 应用实例4 文件/目录 所在组4.1 查看文件/目录所在组4.2修改文件/目录所在的组5 其他组6 改变用户所在组6.1 改变用户所在的组6.2 应用实例7 权限介绍8 rwx权限详解…...

从零到一发布 NPM 包
如果你负责前端的基础能力建设,发布各种功能/插件包犹如家常便饭,所以熟悉对 npm 包的发布与管理是非常有必要的,故此有了本篇总结文章。本篇文章一方面总结,一方面向社区贡献开箱即用的 npm 开发、编译、发布、调试模板ÿ…...
uniapp国际化配置
1、创建资源文件 创建一个locale文件夹,新增index.js,en.json,zh-hans.json 2.配置locale文件夹中的index.js文件 import Vue from vue import VueI18n from vue-i18n// v8.x import en from ./en.json import zhHans from ./zh-Hans.json import zhHant from .…...
前端中 try-catch 捕获不到哪些异常和常见错误
在开发过程中,我们的目标是 0error,0warning。 但有很多因素并不是我们可控的,为了避免某块代码的错误,影响到其他模块或者整体代码的运行,我们经常会使用try-catch模块来主动捕获一些异常或者错误。 比如我们在获取…...

javaEE 初阶 — 如何构造一个 HTTP 请求
文章目录使用 form 表单标签构造1 构造 GET 请求2 构造 POST 请求使用 ajax 构造1 什么是异步2 代码中如何使用 ajax使用第三方工具构造1 postman 工具的安装2 postman 工具的使用使用 form 表单标签构造 1 构造 GET 请求 使用 form 表单构造 HTTP 请求,需要用到两…...

CentOS 7下安装PostgreSQL 15版本数据库(图文详细)
文章目录CentOS 7下安装PostgreSQL 15版本数据库(图文详细)1 简介1.1 概述1.2 官网2 PostgreSQL安装2.1 选定版本2.2 安装依赖2.3 执行安装2.4 初始化2.5 配置环境变量2.6 创建数据库2.6.1 进入命令行2.6.2 创建DB2.6.3 设置密码2.7 配置远程2.8 测试链接3 pgAdmin4工具安装3.1…...

代码随想录算法训练营第五十一天 | 309. 最佳买卖股票时机含冷冻期、714. 买卖股票的最佳时机含手续费
309. 最佳买卖股票时机含冷冻期 动规五部曲 1、确定dp数组以及下标的含义 dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。 具体可以区分出如下四个状态: 状态一:持有股票状态(今天买入股票,或者是…...

中英文拼写检测纠正开源项目使用入门 word-checker 1.1.0
项目简介 word-checker 本项目用于单词拼写检查。支持英文单词拼写检测,和中文拼写检测。 特性说明 可以迅速判断当前单词是否拼写错误 可以返回最佳匹配结果 可以返回纠正匹配列表,支持指定返回列表的大小 错误提示支持 i18n 支持大小写、全角半角…...

面试如果还不会Netty,看这篇文章就够了
我们去面试的时候,经常被问到netty的题目。我整理了netty的32连问。小伙伴们,收藏起来慢慢看吧。 1. Netty是什么,它的主要特点是什么? Netty是一个高性能、异步事件驱动的网络编程框架,它基于NIO技术实现࿰…...
作为大学生,你还不会搭建chatGPT微应用吗?
目录 引言ChatGPT是什么?背景:ChatGPT敢为人先,打破全球僵局示例演示:基于ChatGPT微应用实现的条件及步骤(1)整体框架(2)搭建前的准备工作(3)实际搭建步骤&a…...

Three.js教程:第一个3D场景
推荐:将NSDT场景编辑器加入你3D工具链其他工具系列:NSDT简石数字孪生下面的代码完整展示了通过three.js引擎创建的一个三维场景,在场景中绘制并渲染了一个立方体的效果,为了大家更好的宏观了解three.js引擎, 尽量使用了…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
