第5章 循环和关系表达式
1. strcmp()//比较字符串数组是否相等| string 可以直接用“==”来判断
char word[5] = "aaaa";
strcmp(word,"aaab");//相同输出0,不同输出1;2. 延时函数
#include<ctime>float sec = 2.3;long delay = sec*CLOCKS_PER_SEC;long start = clock();while(clock()-start <delay);cout<<"Hello,world!"<<endl;3.文本读入---p153页
cin---忽略空格和换行符
cin.get()---不忽略
二者都是等到按下回车后,才处理输入缓存区的数据
4. 判断文件尾(EOF)
EOF---Ctrl+Z Enter
1. 采用cin.eof()
如果检测到EOF,则cin.eof() 返回会true,否则返回false;
2. 采用cin.get(ch)
char ch ;
while(cin.get(ch)){//do something}
3. ch = cin.get()
int ch ;while((ch = cin.get())!=EOF){//do something}相关文章:

第5章 循环和关系表达式
1. strcmp()//比较字符串数组是否相等| string 可以直接用“”来判断 char word[5] "aaaa"; strcmp(word,"aaab");//相同输出0,不同输出1; 2. 延时函数 #include<ctime>float sec 2.3;long delay sec*CLOCKS_PER_SEC;long start c…...
中的svg、clipPath、mask元素)
Scalable Vector Graphics (SVG)中的svg、clipPath、mask元素
Scalable Vector Graphics (SVG)是一种用于描述二维向量图形的XML基础标记语言。使用SVG可以实现丰富的图形效果,而不需要像使用位图那样考虑分辨率和像素密度的问题,可以在不同设备上展示出相同的高质量图像。 在SVG中,除了基本形状如circl…...
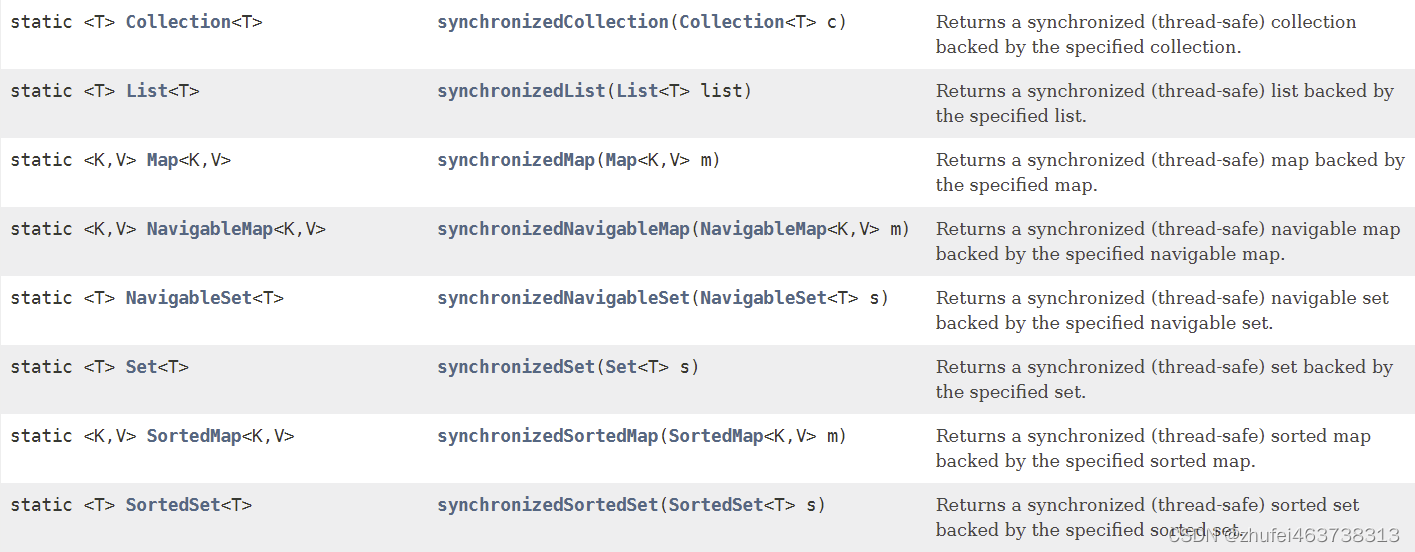
Java基础(十五)集合框架
1. 集合框架概述 1.1 生活中的容器 1.2 数组的特点与弊端 一方面,面向对象语言对事物的体现都是以对象的形式,为了方便对多个对象的操作,就要对对象进行存储。另一方面,使用数组存储对象方面具有一些弊端,而Java 集合…...

安装gitea
1、安装包(gitea-1.13.1-linux-amd64)上传到服务器,并添加执行权限 链接:https://pan.baidu.com/s/1SAxko0RhVmmD21Ev_m5JFg 提取码:ft07 chmod x gitea-1.13.1-linux-amd64 2、执行 ./gitea-1.13.1-linux-amd64 web…...

Java异常处理传递规范总结
java 异常分类 Thorwable类(表示可抛出)是所有异常和错误的超类,两个直接子类为Error和Exception,分别表示错误和异常。其中异常类Exception又分为运行时异常(RuntimeException)和非运行时异常, 这两种异常有很大的区别…...
2d俯视视角游戏,可以切换多种枪械
文章目录 一、 介绍二、 人物移动、鼠标控制转向三、子弹脚本四、子弹随机抛壳五、 爆炸特效六、 发射子弹七、 子弹、弹壳对象池八、 散弹枪九、 火箭弹、发射火箭十、 下载工程文件 一、 介绍 2d俯视视角游戏。 人物视角跟随鼠标移动 多种枪械 抛壳效果 多种设计效果 对象池…...
大四的告诫
保研/考研方向就绩点,(各种)比赛,(考研)刷题为主 工作就算法(比赛),项目,实习为主 👂 LOCK OUT - $atori Zoom/KALONO - 单曲 - 网易云音乐 &…...

滚珠螺杆在设备上的应用
滚珠螺杆跟直线导轨一样,是很多机械设备上不可或缺的重要部件,它是确保机器能够具备高加工精度的前提条件,因此本身对于精度的要求也相当地高。今天,我们就来了解一下滚珠螺杆在不同设备上的应用吧! 1、大型的加工中心…...

Day41线程同步
线程同步 案例:三个窗口卖100张票 //定义一个类SellTicket实现Runnable接口,定义成员变量100张票 public class SellTicket implements Runnable{private int tickets 100;//重写run方法Overridepublic void run(){while (true){ //没有票后&…...

设计模式之享元模式
参考资料 曾探《JavaScript设计模式与开发实践》;「设计模式 JavaScript 描述」享元模式设计模式之享元模式Javascript 设计模式 - 享元模式 定义 享元模式的英文叫:Flyweight Design Pattern。享元设计模式是用于性能优化的模式,这种设计…...
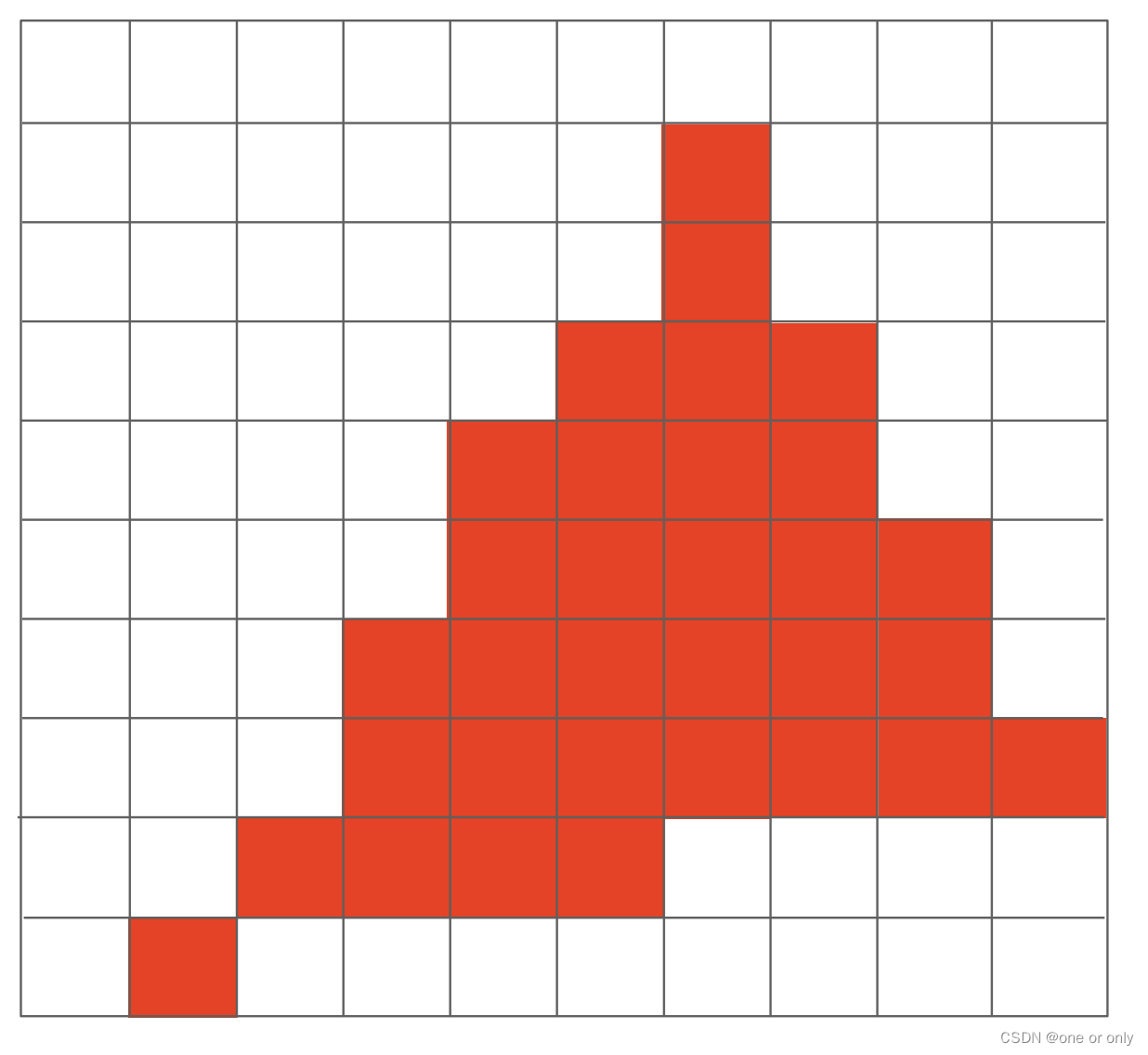
【GAMES101】05 Rasterization(Triangles)
光栅化过程:将一系列变换后的三角形转换为像素的过程。 三角形在图形学中得到很多的应用。 最基础的多边形(边数最少)。任何多边形都可以拆成三角形。性质:三角形内部一定是平面的。三角形内外部定义非常清楚。定义三个顶点后&a…...
)
13. Pod 从入门到深入理解(二)
本章讲解知识点 Pod 容器共享 VolumeConfigMapSecretDownward APIEmptyDir VolumeHostPath Volume1. Pod 容器共享 Volume 1.1. Volume 的背景及需要解决的问题 存储是必不可少的,对于服务运行产生的日志、数据,必须有一个地方进行保存,但是我们的容器每一次重启都是“恢复…...
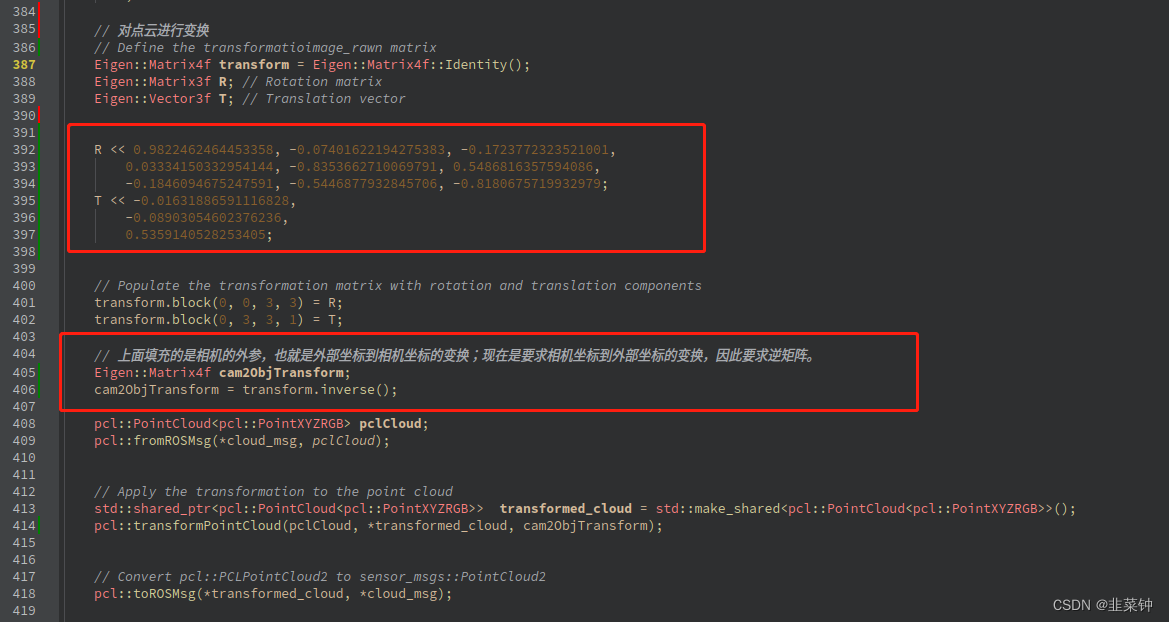
ORBBEC(奥比中光)AstraPro相机在ROS2下的标定与D2C(标定与配准)
文章目录 1.rgb、depth相机标定矫正1.1.标定rgb相机1.2.标定depth相机1.3.rgb、depth相机一起标定(效果重复了,但是推荐使用)1.4.取得标定结果1.4.1.得到的标定结果的意义 1.5.IR、RGB相机分别应用标定结果1.5.1.openCV应用标定结果1.5.2.ros…...

常量与变量:编程中重要的两种数据类型
常量与变量 在编程中,我们常常需要存储一些数据。这些数据有些是恒定不变的,有些却是可以随时变化的。对于恒定不变的数据,我们称之为常量;对于可以变化的数据,我们则称之为变量。这两种数据类型在程序中非常重要&…...
( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数 难度:中等 给定一个包含 n 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。 假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。 你…...

【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...

武忠祥老师每日一题||定积分基础训练(三)
常用的基本不等式: sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...

Docker安装常用软件-Apollo(有问题)
零:apollo概念介绍 官网网站:GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址:mirrors / ctripcorp / apollo GitCode …...

f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点>x0必为|f(x)|的连续点) 注:”[a,b]连续“包括&#…...

今天面了一个来字节要求月薪23K,明显感觉他背了很多面试题...
最近有朋友去字节面试,面试前后进行了20天左右,包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说,80%的人都会栽在第一轮面试,要不是他面试前做足准备,估计都坚持不完后面几轮面试。 其实&…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
