2023年高教社杯数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录
- 0 赛题思路
- 1 描述
- 2 问题概括
- 3 建模过程
- 3.1 边界说明
- 3.2 符号约定
- 3.3 分析
- 3.4 模型建立
- 3.5 模型求解
- 4 模型评价与推广
- 5 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 描述
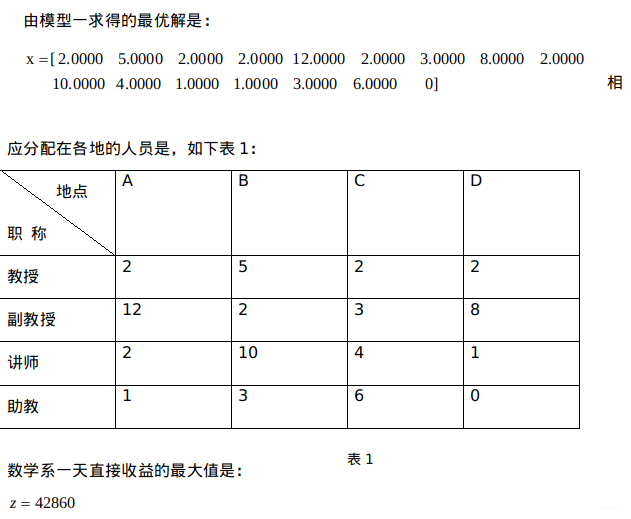
某大学数学系人力资源安排问题是一个整数规划的最优化问题,通过具体分析数学系现有的技术力量和各方面的约束条件,在问题一的求解中,可以列出一天最大直接收益的整数规划,求得最大的直接收益是42860元;而在问题二的求解中,由于教授一个星期只能工作四天,副教授一个星期只能工作五天,在这样的约束条件下,列出一个星期里最大直接收益的整数规划模型,求得其最大直接收益是198720元。
2 问题概括
数学系的教师资源有限,现有四个项目来源于四个不同的客户,工作的难易程度不一,各项目对有关技术人员的报酬不同。所以:
1.在满足工作要求的情况下,如何分配数学系现有的技术力量,使得其一天的直接收益最大?
2.在教授与副教授工作时间受到约束的条件下,如何分配数学系现有的技术力量,使得其在一个星期里的直接收益最大?
3 建模过程
3.1 边界说明
1.不同技术力量的人每天被安排工作的几率是相等的,且相同职称的个人去什么地方工作是随机的;
2.客户除了支付规定的工资额外,在工作期间里,还要支付所有相关的花费(如餐费,车费等);
3.当天工作当天完成.
3.2 符号约定

3.3 分析
由题意可知各项目对不同职称人员人数都有不同的限制和要求.对客户来说质量保证是关键,而教授相对稀缺,因此各项目对教授的配备有不能少于一定数目的限制.其中由于项目技术要求较高,助教不能参加.而两项目主要工作是在办公室完成,所以每人每天有50元的管理费开支.
由以上分析可得:最大直接收益=总收益-技术人员工资-、两地保管费.
3.4 模型建立



3.5 模型求解
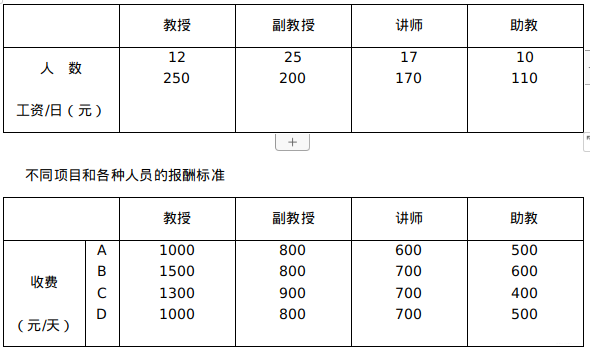
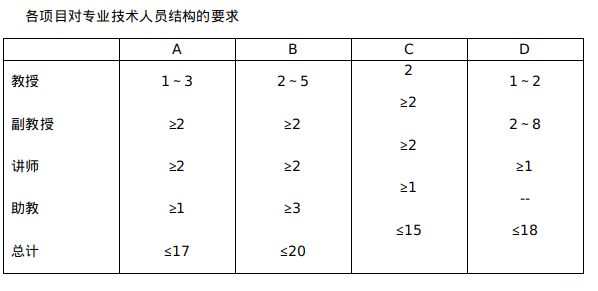
相关数据表格如下:
数学系的职称结构及工资情况
4 模型评价与推广
本模型通过合理的假设,充分考虑各方面的限制条件,得出的人员安排和直接收益
都是本模型的最优解与最优值,对武汉大学数学系的人力资源安排有一定的指导作用。但从模型假设中,我们可以知道对数
学系现有的技术力量的安排是随机的,在相同工作时段里,可能会出现部分人工作次数较多,而部分人较少的不公平情况。
所以在满足工作需求的情况下,分配工作时应该要人为地尽量使得每个人的工作次数不要相差太远,或者相等。
此模型通过对人力资源的调配,从量化的角度得出数学系的最大直接收益。利用此模型的方法可以求出所有类似本模型的线性规划模型。但是,本模型只是单目标的规划,可以在此基础上,增加目标要求。如在数学系的直接收益尽可能大的基础上,使得客户所花费的资金最少,等等。从而建立多目标规划模型。解决更为复杂的实际问题。
5 实现代码
f=[-1000;-800;-550;-450;-1500;-800;-650;-550;-1300;-900;-650;-350;-1000;-800;-650;-450];
A=zeros(9,16);
for i=1:1for j=1:16A(i,j)=1; end
end
for i=2:5for j=i-1:4:11+iA(i,j)=1;end
end
i0=0;
for i=6:9for j=i0+1:(i-5 )*4A(i,j)=1;endi0=j;
end
b=[64;17;20;15;18;12;25;17;10];
Aeq=zeros(1,16);
Aeq(1,3)=1;
beq=[2];
LB=[1;2;2;1;2;2;2;2;2;2;2;1;1;3;1;0];
UB=[3;5;2;2;inf;inf;inf;8;inf;inf;inf;inf;inf;inf;inf;0];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)f=[-1000;-1000;-1000;-1000;-1000;-1000;-1000;-1500;-1500;-1500;-1500;-1500;-1500;-1500;-1250;-1250;-1250;-1250;-1250;-1250;-1250;-950;-950;-950;-950;-950;-950;-950;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-850;-850;-850;-850;-850;-850;-850;-750;-750;-750;-750;-750;-750;-750;-600;-600;-600;-600;-600;-600;-600;-700;-700;-700;-700;-700;-700;-700;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-500;-500;-500;-500;-500;-500;-500;-600;-600;-600;-600;-600;-600;-600;-350;-350;-350;-350;-350;-350;-350;-450;-450;-450;-450;-450;-450;-450];
A=zeros(60,112);
for i=1;1for j=1:112A(i,j)=1;end
end
i0=0;
for i=2:4for j=i0+1:(i-1)*28A(i,j)=1;endi0=j;
end
for i=5:32for j=(i-4):28:80+iA(i,j)=1;end
end
for i=33:39for j= i-32:7:(i-11)A(i,j)=1;end
end
j0=j;
for i=40:46for j=j0+(i-39):7:(i-18)+j0A(i,j)=1;end
end
j0=j;
for i=47:53for j=j0+(i-46):7:j0+(i-25)A(i,j)=1;end
end
j0=j;
for i=54:60for j=j0+(i-53):7:j0+(i-32)A(i,j)=1;end
end
b=[362;48;125;119;17;17;17;17;17;17;17;20;20;20;20;20;20;20;15;15;15;15;15;15;15;18;18;18;18;18;18;18;12;12;12;12;12;12;12;25;25;25;25;25;25;25;17;17;17;17;17;17;17;10;10;10;10;10;10;10];
UB=[3;3;3;3;3;3;3;5;5;5;5;5;5;5;3;3;3;3;3;3;3;2;2;2;2;2;2;2;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;8;8;8;8;8;8;8;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;0;0;0;0;0;0;0];
LB=[1;1;1;1;1;1;1;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;3;3;3;3;3;3;3;1;1;1;1;1;1;1;0;0;0;0;0;0;0];
Aeq=zeros(7,112);
for i=1:7Aeq(i,i+14)=1;
end
beq=[2;2;2;2;2;2;2];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)
建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录 0 赛题思路1 描述2 问题概括3 建模过程3.1 边界说明3.2 符号约定3.3 分析3.4 模型建立3.5 模型求解 4 模型评价与推广5 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 描述 …...
SpringMVC 第二天
第 1 章 ModelAttribute 和 SessionAttribute[ 应 用 ] 1.1ModelAttribute 1.1.1 使用说明 作用: 该注解是 SpringMVC4.3 版本以后新加入的。它可以用于修饰方法和参数。 出现在方法上,表示当前方法会在控制器的方法执行之前,先执行…...

抖音seo短视频矩阵系统源码开发源代码分享--开源-可二开
适用于抖音短视频seo矩阵系统,抖音矩阵系统源码,短视频seo矩阵系统源码,短视频矩阵源码开发,支持二次开发,开源定制,招商加盟SaaS研发等。 功能开发设计 1. AI视频批量剪辑(文字转语音&#x…...

No message found under code ‘-1‘ for locale ‘zh_CN‘.
导出中的报错:No message found under code -1 for locale zh_CN. 报错原因:页面中展示的数据和后端excel中的数据不一致导致 具体原因:...
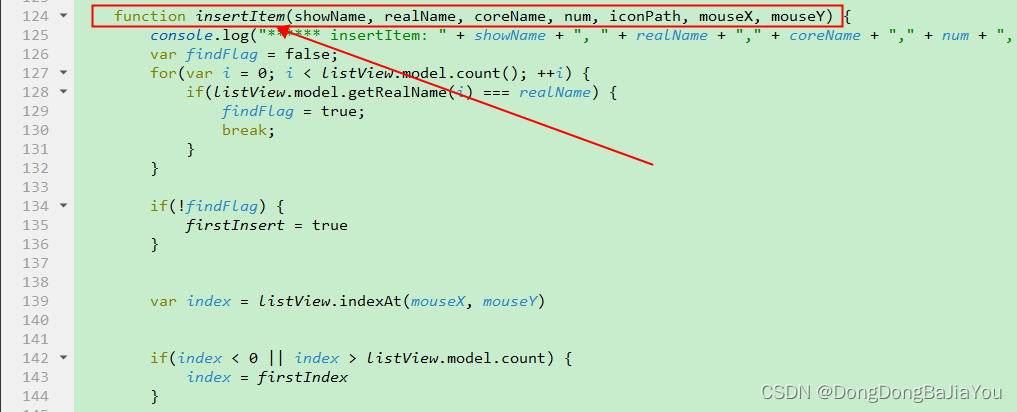
QtWidgets和QtQuick融合(QML与C++融合)
先放一个界面效果吧! 说明:该演示程序为一个App管理程序,可以将多个App进行吸入管理。 (动画中的RedRect为一个带有QSplashScreen的独立应用程序) 左侧边栏用的是QQuickView进行.qml文件的加载(即QtQuick…...

基于Vue的3D饼图
先看效果: 再看代码: <template><div class"container"><div style"height: 100%;width: 100%;" id"bingtu3D"></div></div></template> <script> import "echarts-liqu…...

Gateway简述
前言 在微服务架构中,一个系统会被拆分为很多个微服务。那么作为客户端调用多个微服务接口的地址。另外微服务架构的请求中,90%的都携带认证信息/用户登录信息,都需要做相关的限制管理,API网关由此应允而生。 这样的架构会存…...
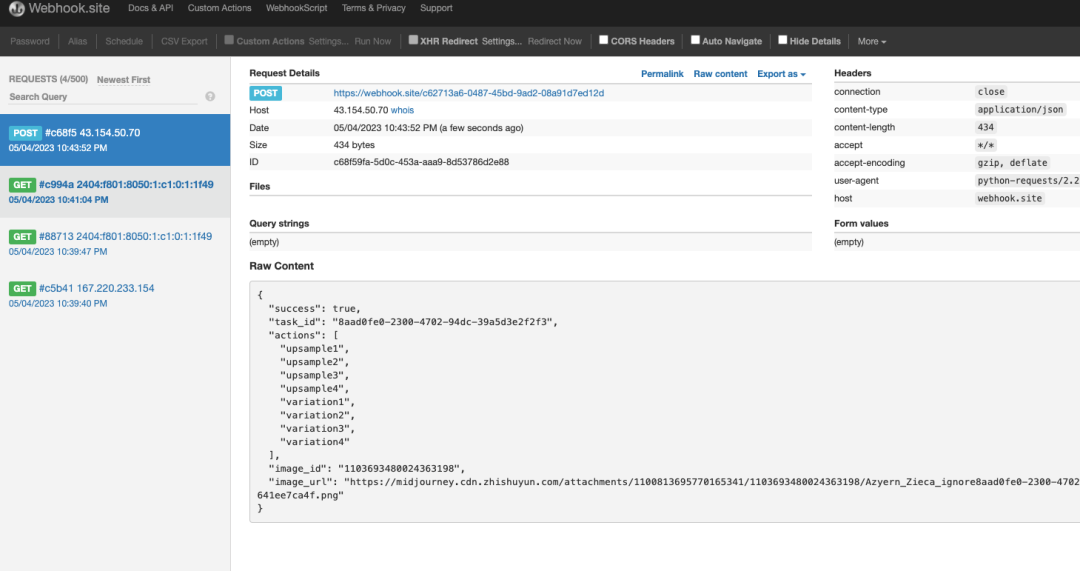
Midjourney API 的对接和使用
“ 阅读本文大概需要 4 分钟。 ” 在人工智能绘图领域,想必大家听说过 Midjourney 的大名吧。 Midjourney 以其出色的绘图能力在业界独树一帜。无需过多复杂的操作,只要简单输入绘图指令,这个神奇的工具就能在瞬间为我们呈现出对应的图像。无…...

01 消息引擎系统
本文是Kafka 核心技术与实战学习笔记 kafka的作用 kafka最经常被提到的作用是是削峰填谷,即解决上下游TPS的错配以及瞬时峰值流量,如果没有消息引擎系统的保护,下游系统的崩溃可能会导致全链路的崩溃。还有一个好处是发送方和接收方的松耦合…...
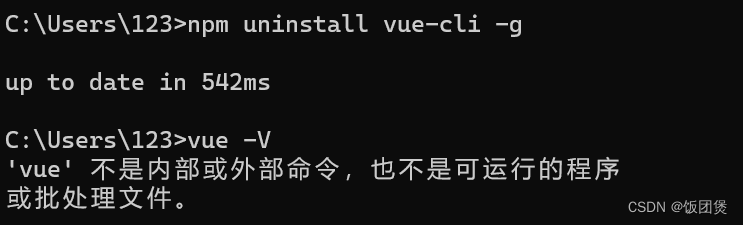
npm 卸载 vuecli后还是存在
运行了npm uninstall vue-cli -g,之后是up to date in,然后vue -V,版本号一直都在,说明没有卸载掉 1、执行全局卸载命令 npm uninstall vue-cli -g 2、删除vue原始文件 查看文件位置,找到文件删掉 where vue 3、再…...

Unity 之利用 localEulerAngle与EulerAngle 控制物体旋转
文章目录 概念讲解localEulerAngle与EulerAngle的区别 概念讲解 欧拉角(Euler Angles)是一种常用于描述物体在三维空间中旋转的方法。它使用三个角度来表示旋转,分别绕物体的三个坐标轴(通常是X、Y和Z轴)进行旋转。这…...
)
从零学算法 (剑指 Offer 13)
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如&am…...

854之数据结构
一.线性表 1.顺序表 #include <iostream> #include<stdlib.h> using namespace std; #define max 100 typedef struct {int element[max];int last; } List; typedef int position ; void Insert(int x, position p, List &L) {position q;if (L.last > ma…...
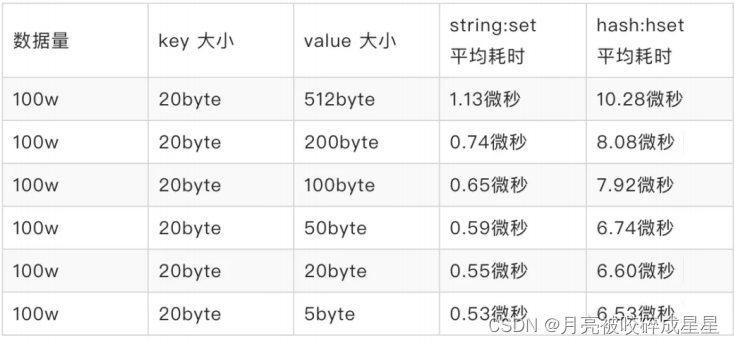
Redis从基础到进阶篇(二)----内存模型与内存优化
目录 一、缓存通识 1.1 ⽆处不在的缓存 1.2 多级缓存 (重点) 二、Redis简介 2.1 什么是Redis 2.2 Redis的应用场景 三、Redis数据存储的细节 3.1 Redis数据类型 3.2 内存结构 3.3 内存分配器 3.4 redisObject 3.4.1 type 3.4.2 encoding 3…...
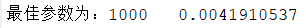
DBO优化SVM的电力负荷预测,附MATLAB代码
今天为大家带来一期基于DBO-SVM的电力负荷预测。 原理详解 文章对支持向量机(SVM)的两个参数进行优化,分别是:惩罚系数c和 gamma。 其中,惩罚系数c表示对误差的宽容度。c越高,说明越不能容忍出现误差,容易过拟合。c越小࿰…...

第一百二十五回 dart中List和Map的常见用法
文章目录 概念介绍使用方法初始化相互转换元素操作 经验分享 我们在上一章回中介绍了Flexible组件相关的内容,本章回中将介绍 dart中的List和Map.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在这里介绍的List也叫列表,它表示一组相…...
小白到运维工程师自学之路 第七十九集 (基于Jenkins自动打包并部署Tomcat环境)2
紧接上文 4、新建Maven项目 clean package -Dmaven.test.skiptrue 用于构建项目并跳过执行测试 拉到最后选择构建后操作 SSH server webExec command scp 192.168.77.18:/root/.jenkins/workspace/probe/psi-probe-web/target/probe.war /usr/local/tomcat/webapps/ /usr/loca…...
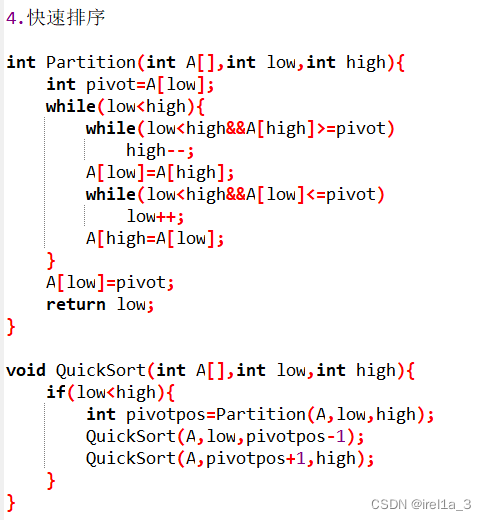
林【2021】
三、应用 1.字符串abaaabaabaa,用KMP改进算法求出next和nextval的值 2.三元组矩阵 4.二叉树变森林 四、代码(单链表递增排序,二叉树查找x,快速排序)...
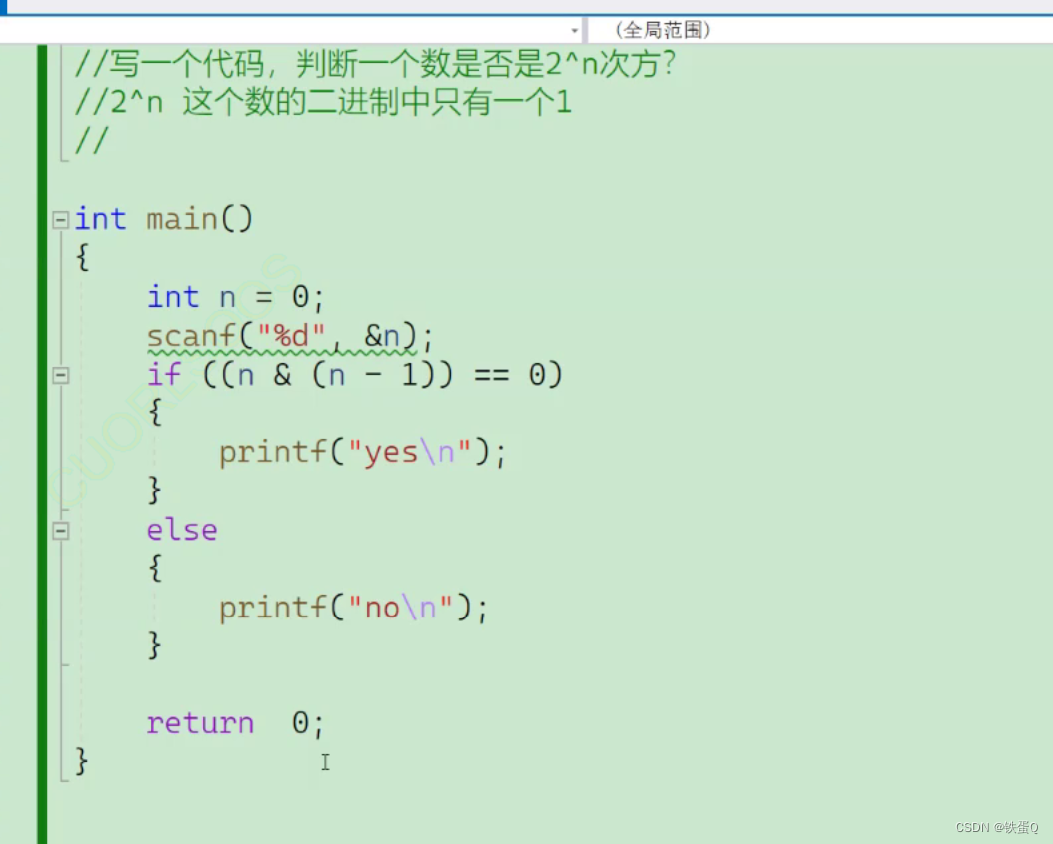
c语言练习题30:判断一个数是否为2^n
判断一个数是否为2^n 思路:2^n中只有一个1故可以通过n&(n-1)是否为0来判断。 代码:...

VX小程序 实现区域转图片预览
图例 方法一 1、安装插件 wxml2canvas npm install --save wxml2canvas git地址参照:https://github.com/wg-front/wxml2canvas 2、类型 // 小程序页面 let data{list:[{type:wxml,class:.test_center .draw_canvas,limit:.test_center,x:0,y:0}] } 3、数据结…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
