java面试题-Dubbo和zookeeper运行原理
远离八股文，面试大白话，通俗且易懂
看完后试着用自己的话复述出来。有问题请指出，有需要帮助理解的或者遇到的真实面试题不知道怎么总结的也请评论中写出来，大家一起解决。
java面试题汇总-目录-持续更新中
分布式注册中心和服务调用的原理大多如此：
1.Dubbo和zookeeper运行原理
1.首先搞懂zookeeper和dubbo框架中的角色
Provider: 暴露服务的服务提供方【服务提供方】
Consumer: 调用远程服务的服务消费方【服务消费方】
Registry: 服务注册与发现的注册中心。
Monitor: 统计服务的调用次调和调用时间的监控中心。
Container: 服务运行容器
2. 运行原理逻辑
1.首先容器负责启动、加载、运行服务提供者
2.服务提供者在启动时，向注册中心注册自己提供的服务接口
3.服务消费者在启动时，向注册中心订阅自己需要的服务接口
4.注册中心将消费者所需的接口地址列表返回给消费者，如果有变更，则基于长连接将变更数据更新给消费者。
5.消费者从提供者列表中国，基于负载均衡算法，选择一台提供者进行调用，如果失败会重试另外一台（提供者列表是指zookeeper分布式集群部署）
6.服务消费者和提供者，会在本地内存中累计调用次数和调用时间，然后定时每分钟会发送到监控中心
相关文章：
java面试题-Dubbo和zookeeper运行原理
远离八股文，面试大白话，通俗且易懂 看完后试着用自己的话复述出来。有问题请指出，有需要帮助理解的或者遇到的真实面试题不知道怎么总结的也请评论中写出来，大家一起解决。 java面试题汇总-目录-持续更新中 分布式注册中心和服务调…...
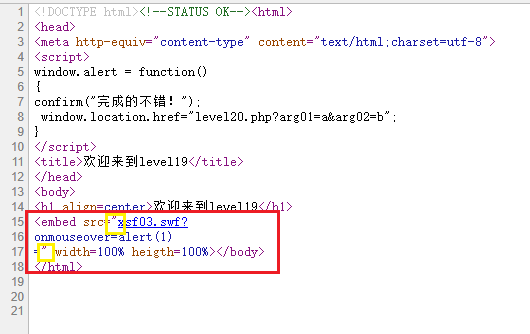
XSS漏洞 深度解析 XSS_labs靶场
XSS漏洞 深度解析 XSS_labs靶场 0x01 简介 XSS原名为Cross-site Sciprting(跨站脚本攻击)，因简写与层叠样式表(Cascading style sheets)重名，为了区分所以取名为XSS。 这个漏洞主要存在于HTML页面中进行动态渲染输出的参数中，利用了脚本语…...
C++的左值、右值、左值引用和右值引用
目录 左值和右值左值引用右值引用 参考《现代C语言核心特性解析》 以下加粗文字都是摘自本书。 左值和右值 左值和右值得概念在C98就出现了，根据字面意思理解就是：左值是表达式等号左边的值，右值是表达式等号右边的值。 int x 1; int y …...
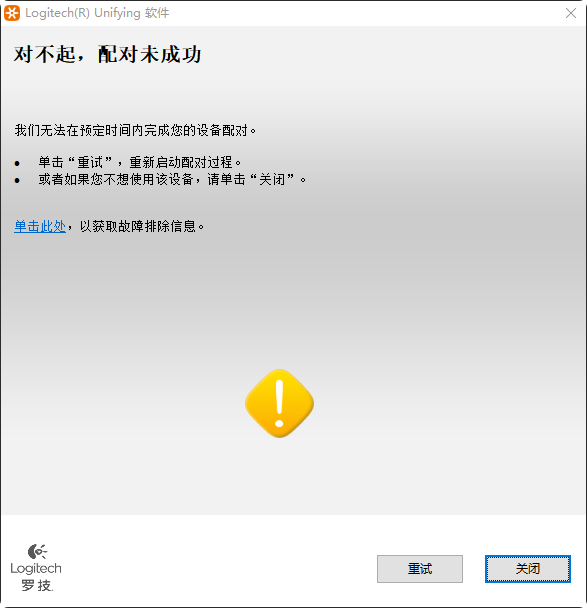
罗技鼠标使用接收器和电脑重新配对
罗技鼠标使用接收器和电脑重新配对 文章目录 罗技鼠标使用接收器和电脑重新配对1\. 前言2\. 安装软件3\. 进行配对3.1. 取消之前的配对3.2. 重新配对3.3 配对完成 4\. 报错4.1. 重新配对时显示配对未成功 1. 前言 罗技的鼠标出厂的时候，默认的是将通道一设置为接收…...
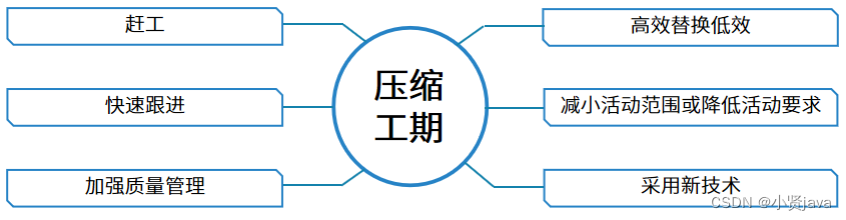
高项备考葵花宝典-项目进度管理输入、输出、工具和技术(下，很详细考试必过)
项目进度管理的目标是使项目按时完成。有效的进度管理是项目管理成功的关键之一，进度问题在项目生命周期内引起的冲突最多。 小型项目中，定义活动、排列活动顺序、估算活动持续时间及制定进度模型形成进度计划等过程的联系非常密切，可以视为一…...
GumbleSoftmax感性理解--可导式输出随机类别
GumbleSoftmax 本文不涉及GumbleSoftmax的具体证明和推导，有需要请参见1，只是从感性角度来直观讲解为何要引入GumbleSoftmax，同时又为什么不用Gumblemax。 GumbleSoftmax提出是为了应对分布采样不可导的问题。举例而言，我们从网络…...
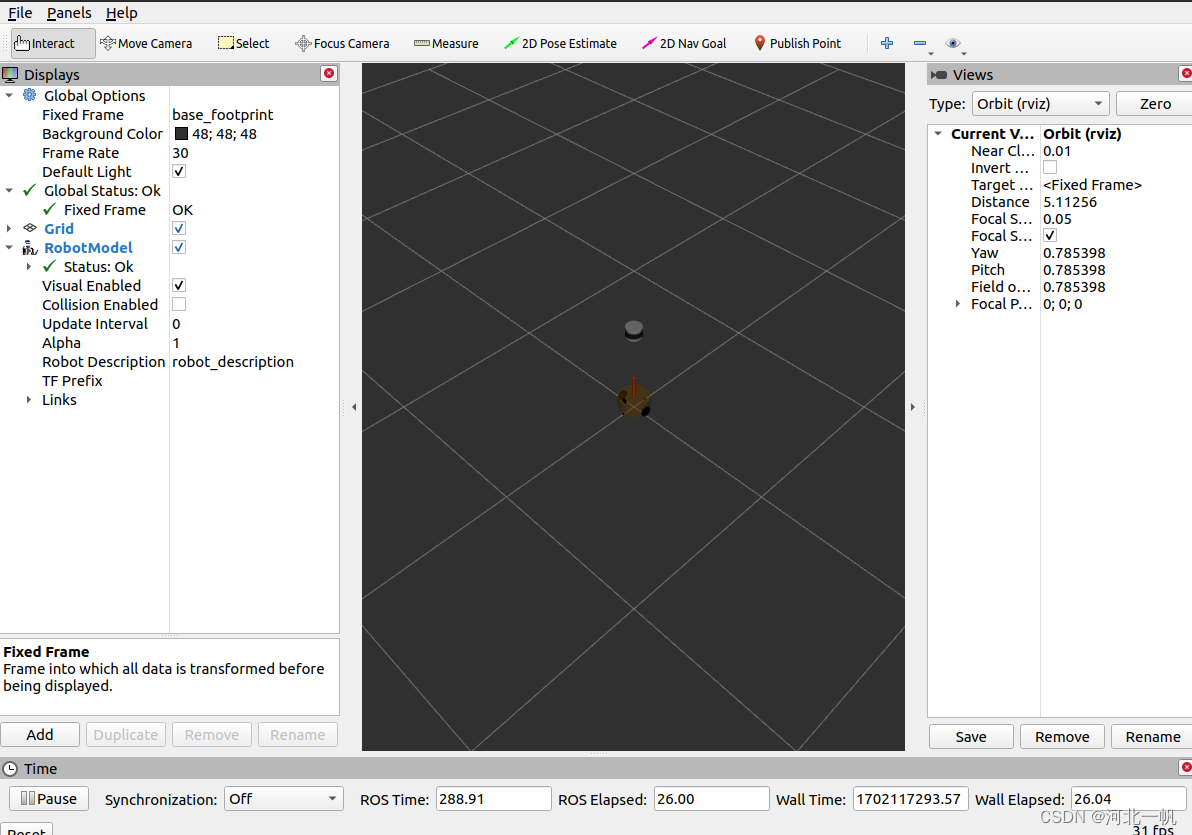
ROS gazebo 机器人仿真，环境与robot建模，添加相机 lidar，控制robot运动
b站上有一个非常好的ros教程234仿真之URDF_link标签简介-机器人系统仿真_哔哩哔哩_bilibili，推荐去看原视频。 视频教程的相关文档见：6.7.1 机器人运动控制以及里程计信息显示 Autolabor-ROS机器人入门课程《ROS理论与实践》零基础教程 本文对视频教程…...
人体关键点检测3：Android实现人体关键点检测(人体姿势估计)含源码 可实时检测
目录 1. 前言 2.人体关键点检测方法 (1)Top-Down(自上而下)方法 (2)Bottom-Up(自下而上)方法： 3.人体关键点检测模型训练 4.人体关键点检测模型Android部署 （1） 将Pytorch模型转换ONNX模型 （2） 将ONNX模型转换…...
踩坑记录：uniapp中scroll-view的scroll-top不生效问题；
情景描述： 最近在uniapp项目中用到scroll-view内置组件，有需求是在页面下拉刷新后，让scroll-view组件区域的显示内容置顶，也就是scroll-view区域的内容恢复不滑动的状态； 补充：下拉刷新操作scroll-view组件…...
YOLOX 学习笔记
文章目录 前言一、YOLOX贡献和改进二、YOLOX架构改进总结 前言 在计算机视觉领域，实时对象检测技术一直是一个热门的研究话题。YOLO（You Only Look Once）系列作为其中的佼佼者，以其高效的检测速度和准确性，广泛应用于…...
第3节：Vue3 v-bind指令
实例： <template><div><button v-bind:disabled"isButtonDisabled">点击我</button></div> </template><script> import { ref } from vue;export default {setup() {const isButtonDisabled ref(false);ret…...
Token 和 N-Gram、Bag-of-Words 模型释义
ChatGPT（GPT-3.5）和其他大型语言模型（Pi、Claude、Bard 等）凭何火爆全球？这些语言模型的运作原理是什么？为什么它们在所训练的任务上表现如此出色？ 虽然没有人可以给出完整的答案，但…...
【go语言实践】基础篇 - 流程控制
if语句 go里面if不需要括号将条件表达式包含起来，这与python也有点类似 if 条件表达式 { } if num > 18 {// ... } else if num > 20 {// ... } else {// ... }需要注意的是go支持在if的条件表达式中直接定义一个变量，变量的作用域只在if范围内…...
Linux：gdb的简单使用
个人主页 ： 个人主页 个人专栏 ： 《数据结构》 《C语言》《C》《Linux》 文章目录 前言一、前置理解二、使用总结 前言 gdb是Linux中的调试代码的工具 一、前置理解 我们都知道要调试一份代码，这份代码的发布模式必须是debug。那你知道在li…...
NestJS的微服务实现
1.1 基本概念 微服务基本概念：微服务就是将一个项目拆分成多个服务。举个简单的例子：将网站的登录功能可以拆分出来做成一个服务。 微服务分为提供者和消费者，如上“登录服务”就是一个服务提供者，“网站服务器”就是一个服务消…...
Debian 终端Shell命令行长路径改为短路径
需要修改bashrc ~/.bashrc先备份一份 cp .bashrc bashrc.backup编辑bashrc vim ~/.bashrc可以看到bashrc内容为 # ~/.bashrc: executed by bash(1) for non-login shells. # see /usr/share/doc/bash/examples/startup-files (in the package bash-doc) # for examples# If…...
Ansible变量是什么？如何实现任务的循环？
Ansible 利用变量存储整个 Ansible 项目文件中可重复使用的值，从而可以简化项目的创建和维护，并减少错误的发生率。在定义Ansible变量时，通常有如下三种范围的变量： global范围：从命令行或Ansible配置中设置的变量&am…...
随机梯度下降的代码实现
在单变量线性回归的机器学习代码中，我们讨论了批量梯度下降代码的实现，本篇将进行随机梯度下降的代码实现，整体和批量梯度下降代码类似，仅梯度下降部分不同： import numpy as np import pandas as pd import matplotl…...
渐进推导中常用的一些结论
标题很帅 STAR-RIS Enhanced Joint Physical Layer Security and Covert Communications for Multi-antenna mmWave Systems文章末尾的一个推导。 lim M → ∞ ∥ Φ ( w k ⊗ Θ r ) Ω r w H g ∗ ∥ 2 2 M lim M → ∞ Tr ( g T Ω r w ( w k ⊗ Θ r ) H Φ H Φ…...
网络安全等级保护V2.0测评指标
网络安全等级保护（等保V2.0）测评指标： 1、物理和环境安全 2、网络和通信安全 3、设备和计算安全 4、应用和数据安全 5、安全策略和管理制度 6、安全管理机构和人员 7、安全建设管理 8、安全运维管理 软件全文档获取：点我获取 1、物…...
在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中，时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志，到供应链系统的物流节点时间戳，时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库，其日期时间类型的…...
2021-03-15 iview一些问题
1.iview 在使用tree组件时，发现没有set类的方法，只有get，那么要改变tree值，只能遍历treeData，递归修改treeData的checked，发现无法更改，原因在于check模式下，子元素的勾选状态跟父节…...
PL0语法，分析器实现！
简介 PL/0 是一种简单的编程语言，通常用于教学编译原理。它的语法结构清晰，功能包括常量定义、变量声明、过程（子程序）定义以及基本的控制结构（如条件语句和循环语句）。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言，由 Niklaus Wirth 设计，用于展示编译原理的核…...
C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全（Thread Safety） 线程安全是指在多线程环境下，某个函数、类或代码片段能够被多个线程同时调用时，仍能保证数据的一致性和逻辑的正确性…...
Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系，以下是深入解析： 门铃FIFO溢出的本质 在RapidIO系统中，门铃消息FIFO是硬件控制器内部的缓冲区，用于临时存储接收到的门铃消息（Doorbell Message）。…...
安卓基础（aar）
重新设置java21的环境，临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的： MyApp/ ├── app/ …...
视频行为标注工具BehaviLabel（源码+使用介绍+Windows.Exe版本）
前言： 最近在做行为检测相关的模型，用的是时空图卷积网络（STGCN），但原有kinetic-400数据集数据质量较低，需要进行细粒度的标注，同时粗略搜了下已有开源工具基本都集中于图像分割这块，…...
现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？
现有的 Redis 分布式锁库（如 Redisson）相比于开发者自己基于 Redis 命令（如 SETNX, EXPIRE, DEL）手动实现分布式锁，提供了巨大的便利性和健壮性。主要体现在以下几个方面： 原子性保证 (Atomicity)ÿ…...
CVPR2025重磅突破：AnomalyAny框架实现单样本生成逼真异常数据，破解视觉检测瓶颈！
本文介绍了一种名为AnomalyAny的创新框架，该方法利用Stable Diffusion的强大生成能力，仅需单个正常样本和文本描述，即可生成逼真且多样化的异常样本，有效解决了视觉异常检测中异常样本稀缺的难题，为工业质检、医疗影像…...
ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念： 1）ZYNQ全称：ZYNQ7000 All Pgrammable SoC 2）SoC:system on chips(片上系统)，对比集成电路的SoB（system on board） 3）ARM：处理器…...